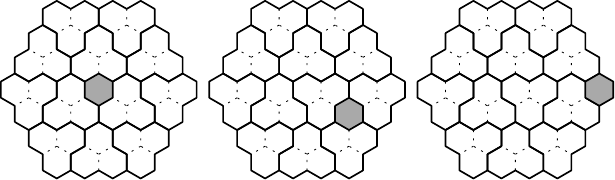
Gegeben sind sechs Schachteln, die von 1 bis 6 nummeriert sind, und 17 Pfirsiche, die auf unbekannte Weise auf diese Schachteln verteilt sind. Uns ist nur die folgende Vorgehensweise erlaubt: Sind genau Pfirsiche in der -ten Schachtel, essen wir einen davon und geben anschließend die verbleibenden Pfirsiche in die Schachteln bis , und zwar genau einen Pfirsich in jede der Schachteln. Wie müssen die Pfirsiche am Anfang auf die sechs Schachteln verteilt sein, sodass wir alle Pfirsiche essen können?Lösung
Ergebnis:
Am besten geht man das Problem umgekehrt an: Die Endverteilung , bei der alle Pfirsiche gegessen wurden, kann nur ausgehend von der Verteilung erreicht werden. Diese kann wiederum nur aus hervorgehen, usw. Auf diesem Weg kann eine eindeutige Folge von Verteilungen der Pfirsiche erzeugt werden:
|
|
|
Diese Folge endet mit der gesuchten Anfangsverteilung .