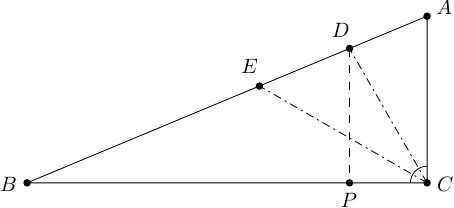
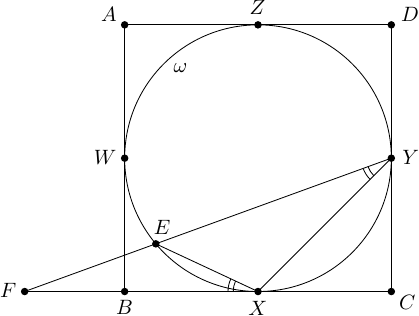
Ergebnis:
Die Bedingung kann ebenso als geschrieben werden. Im Folgenden beziehen sich sämtliche Kongruenzen auf den Modul . Da eine Primzahl ist, gibt es für jede positive ganze Zahl genau eine positive ganze Zahl kleiner als , geschrieben als , für die gilt, und deshalb für zwei Zahlen stets genau eine Zahl mit , nämlich diejenige Zahl mit .
Sei zunächst ein Lösungstripel mit ausschließlich positiven ganzen Zahlen , und . Man setzt nun die Darstellungen und mit eindeutig definierten Zahlen in die Kongruenzrelation ein und erhält , was nach Multiplikation mit zu führt. Eine weitere Multiplikation mit liefert schließlich
|
Da alle gemachten Umformungen Äquivalenzumformungen waren, gibt es umgekehrt für jede Wahl von zwei Zahlen genau ein und im Fall, dass ist, genau ein und genau ein , so dass das Tripel die geforderte Bedingung erfüllt. Dabei tritt der Fall genau dann ein, wenn gilt. Von den insgesamt Möglichkeiten, Paare mit zu wählen, müssen also Möglichkeiten wegen der Paare mit abgezogen werden. Folglich gibt es Lösungstripel mit .
Sei nun und . In diesem Fall reduziert sich die gegebene Kongruenz zu und es gibt genau dann eine Lösung, wenn gilt. Die Anzahl dieser Lösungstripel mit ist . In analoger Weise erhält man auch je Lösungstripel im Fall mit und mit . Somit gibt es Lösungstripel , in denen genau ein Mal die Null vorkommt.
Falls zwei der Einträge in einem Lösungstripel null sind, so folgt daraus, dass der dritte Eintrag auch null sein muss. Also gibt es noch die Lösung .
Aus dieser vollständigen Fallunterscheidung ergibt sich die Gesamtanzahl der gesuchten Tripel zu
|