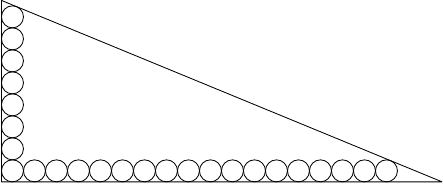
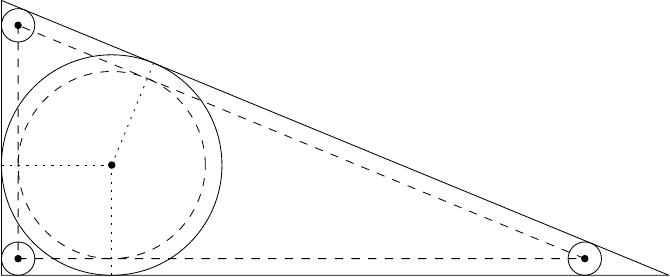
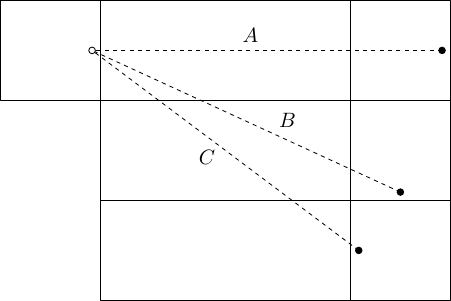
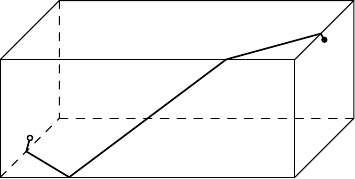
Ein gleichseitiges Dreieck mit der Seitenlänge wird in kleine gleichseitige Dreiecke mit der Seitenlänge zerlegt. Wir nennen eine Menge von Ecken dieser kleinen Dreiecke unabhängig, falls für zwei verschiedene Punkte die Strecke nicht parallel zu irgendeiner Seite von ist. Was ist die größte Anzahl an Elementen, die eine unabhängige Menge haben kann?Lösung
Ergebnis:
1346
Jeder Ecke auf dem Gitter kann ihr Abstand zu den drei Seiten von zugeordnet werden. Dabei wählt man als Einheit die Höhe eines kleinen gleichseitigen Dreiecks. Es ist leicht zu sehen, dass sich für jede Ecke diese drei Abstände zu addieren. Hat man andererseits ein Tripel aus nicht-negativen ganzen Zahlen, die sich zu aufsummieren, dann gibt es eine eindeutig bestimmte Ecke im Gitter, welche die Einträge aus dem Tripel als Abstände zu den Seiten von besitzt. Diese Zahlentripel zu betrachten ist deshalb äquivalent dazu, die Ecken zu betrachten. Im Folgenden werden die Tripel betrachtet und deren Einträge als Koordinaten bezeichnet.
Die Bedingung für eine unabhängige Menge ist, dass keine zwei Tripel in der Menge dieselbe erste, zweite oder dritte Koordinate haben. Sei
|
eine unabhängige Menge. Da die Zahlen verschiedene nicht-negative ganze Zahlen sind, beträgt deren Summe mindestens
|
Dasselbe gilt auch für die Summen und . Wegen der Bedingung für alle ergibt sich somit die Abschätzung
|
Daraus erhält man
und schließlich .
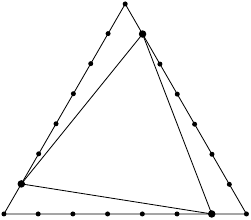
Dass das Maximum für wirklich angenommen werden kann, zeigt das Beispiel hier: Die beiden Folgen von Punkten
|
bilden zusammen eine unabhängige Menge mit
Elementen. Folglich lautet die Antwort
.
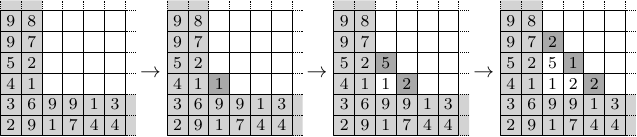
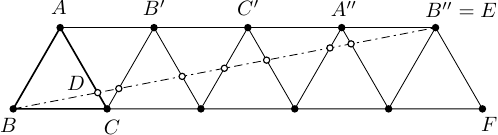
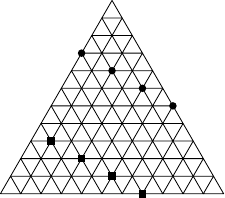
Die folgende Grafik zeigt eine Konstruktion einer unabhängigen Menge für ein Dreieck mit Seitenlänge :