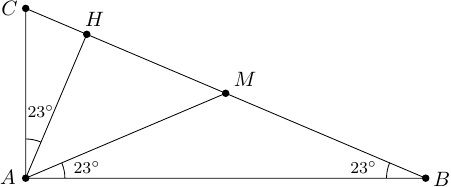
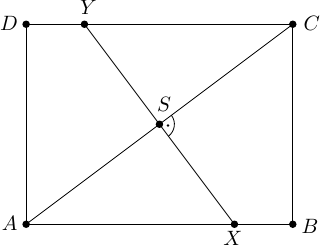
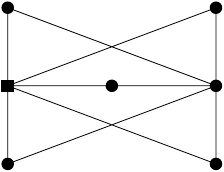
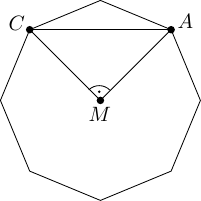
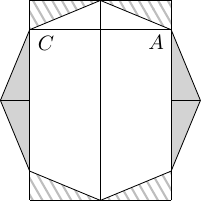
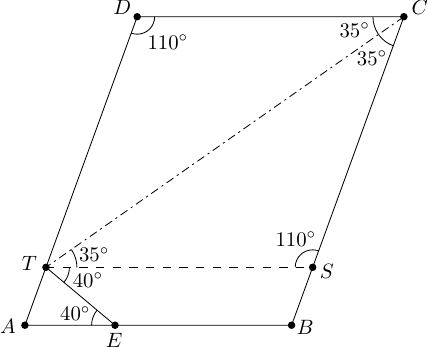
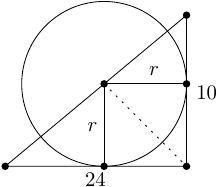
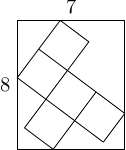
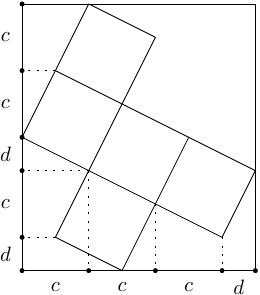
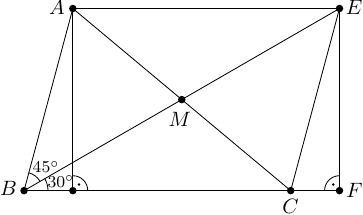
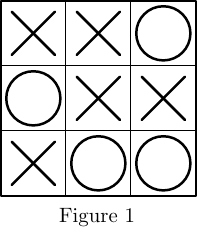
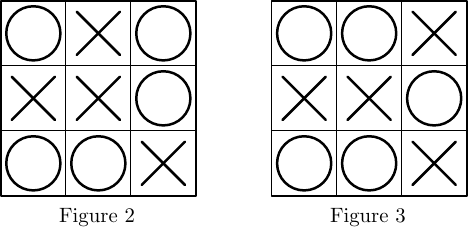
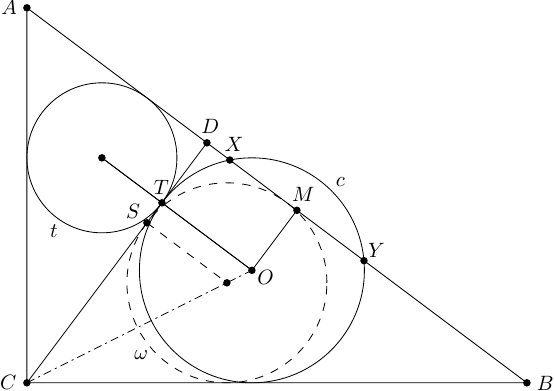
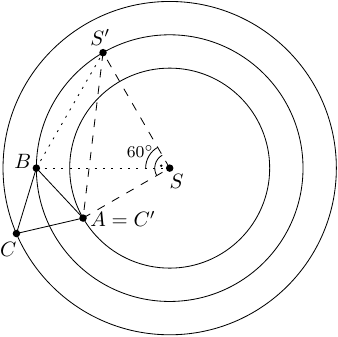
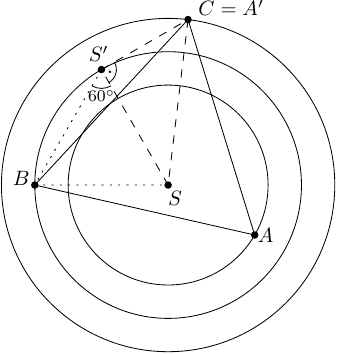
Ergebnis:
Zuerst multipliziert man die erste Gleichung mit und verwendet die zweite Gleichung um zu bekommen. Wir merken an, dass sowohl als auch eine Primzahl ist. Da die Klammerausdrücke jeweils größer als sind, muss einer der beiden und der andere sein, wobei . Wir nehmen zuerst an, dass und für fixierte , mit . Dann gilt , und . Es ist dann leicht zu überprüfen, dass
|
die Bedingung erfüllt und daher eine gültige Lösung des Problems für jedes und liefert. Wir zeigen noch, dass all diese Lösungen verschieden sind. Nehmen wir an, dass zwei Paare und die gleiche Lösung liefern. Dann gilt und , wodurch und gelten muss. Ähnlich verfahren wir mit dem Fall und . Auch hier erhalten wir verschiedene Lösungen
|
für und . Keine der Lösungen aus diesem Fall ist gleich einer Lösung aus dem anderen Fall, da für kein und aus unserem Wertebereich gilt. Daher gibt es insgesamt Lösungen.