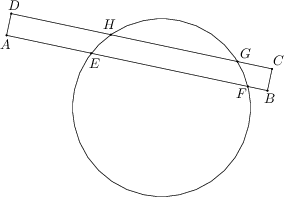
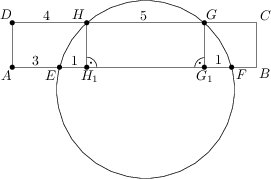
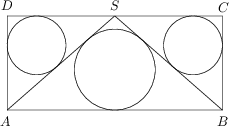
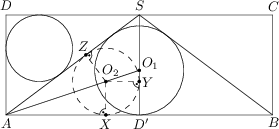
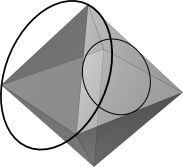
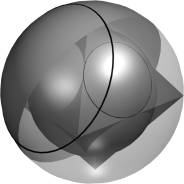
Ergebnis:
Stellt man Gleichungen auf, so findet man zwei Lösungen (abhängig davon, ob es draußen regnet oder nicht), von denen eine nicht funktioniert, da Inder Tee trinken würden, was unmöglich ist. Die andere Lösung funktioniert und deshalb trinken Inder Tee:
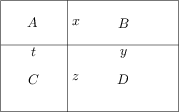
Bezeichnet man die Anzahl der Türken, die Kaffee trinken, mit , die Anzahl der Türken, die Tee trinken, mit , die Anzahl der Inder, die Kaffee trinken, mit , und die Anzahl der Inder, die Tee trinken, mit , so kann man unter der Annahme, dass es draußen regnet, folgende Gleichungen finden:
Subtrahiert man die letzte Gleichung von der Summe der drei ersten, so erhält man und hieraus die Lösungen und . Analoge Überlegungen führen unter der Annahme, dass es draußen nicht regnet, auf den Widerspruch .