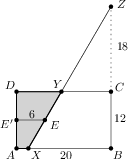
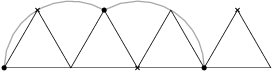
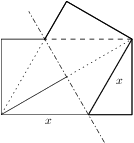
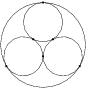
Aufgabenstellungen und Lösungen

Ergebnis:

$700\%$

Die Verlängerung einer Seite um $100\%$ ist gleichbedeutend mit einer Multiplikation mit 2. Beträgt das ursprüngliche Volumen des Würfels $a^3$, so ist es nach der Verlängerung der Seite ${(2a)}^3=8a^3$. Also ist das Volumen um $7a^3$ gewachsen, was einer Zunahme um $700\%$ entspricht.

Ergebnis:

9

Wenn man die Geraden so wählt, dass sich je zwei Geraden in einem Schnittpunkt innerhalb des Ringes schneiden und zugleich alle Geraden Sekanten des inneren Kreises sind, so entstehen neun Teile. Mehr sind nicht möglich.

Ergebnis:

$3\cdot 2=6$

Es ist $72=8\cdot 9$. Aus der Teilbarkeit durch $8$ folgt $b=2$. Die Teilbarkeit durch $9$ liefert die Bedingung $9\mid (a+6+7+9+2)$, woraus $a=3$ folgt.

Also ist $a\cdot b=6$.

Ergebnis:

25

Die Anzahl der Schüler ist durch $5$ teilbar und größer als $20$ (Schubfachprinzip). $25$ ist aber bereits ausreichend.

Ergebnis:

$38,4\%=48∕125$

Man betrachtet das, was übrig bleibt, wenn alle Würfel mit Schokoladenüberzug gegessen wurden. Dies ist ein Quader mit den Seitenlängen $8$, $8$ und $3$, der nur aus Würfeln ohne Schokolade besteht. Insgesamt sind dies $192$ Würfel. Von allen $10\cdot 10\cdot 5=500$ Würfeln ist dies ein Anteil von $192∕500\cdot 100\%=38,4\%$.

Ergebnis:

$\sqrt{10}$

Die längste Diagonale ist $\mathit{CX}$ (oder auch $\mathit{DX}$). Sei $E$ der Lotfußpunkt des Lotes von $X$ auf $\mathit{BC}$. Da das Dreieck $\mathit{AXB}$ nach dem Satz des Pythagoras rechtwinklig ist, ist $\overline{\mathit{EB}}=\overline{\mathit{EX}}=1$. Das Dreieck $\mathit{ECX}$ ist ebenfalls rechtwinklig und mit dem Satz des Pythagoras folgt $\overline{\mathit{XC}}=\sqrt{3^2+1^2}=\sqrt{10}$.

Ergebnis:

2012

Probiert man die $16$ Möglichkeiten auf der rechten Seite durch, so sieht man, dass nur $4\cdot 503=2012$ möglich ist. Der Suchprozess kann durch verschiedene Beobachtungen beschleunigt werden, z.B. muss das Ergebnis mit $2$ beginnen, weshalb auf der linken Seite die erste Zahl $4$ sein muss und die zweite mit $5$ beginnen muss.

Ergebnis:

300

O.B.d.A. sei $x\ge y$. Dann ist

Dies kann durch $x=y=100$ auch erreicht werden.

Ergebnis:

5

Addiert man die beiden Gleichungen für das jeweilige AM, so erhält man

Division durch $3$ ergibt das Ergebnis $5$.

Ergebnis:

45

Man ordnet die Bäume nach ihrem Abstand zum Gärtner und prüft jeden einzelnen der Reihe nach auf Sichtbarkeit. Wenn ein Baum noch nicht ausgestrichen wurde, kennzeichnet man ihn als sichtbar und streicht alle Bäume, die mit diesem auf einer Geraden liegen. Er kann dann insgesamt $45$ Bäume sehen.

Ergebnis:

$1+1+2+2+2+1+1=10$

Wir unterscheiden die Würfel nach der Anzahl der schwarzen Seiten und deren Lage zueinander. Für $0$ schwarze Seiten gibt es eine Möglichkeit, ebenso für eine schwarze. Für zwei schwarze Seiten gibt es zwei Möglichkeiten, entweder sie sind benachbart oder nicht, d.h. sie liegen gegenüber. Für drei schwarze Seiten gibt es ebenfalls zwei Möglichkeiten: Die schwarzen Seiten stoßen an einer gemeinsamen Ecke zusammen oder nicht. Für $4,5$ und $6$ schwarze Seiten haben wir eine symmetrische Situation zu $2,1$ bzw. $0$ schwarze Seiten. Insgesamt gibt es also $1+1+2+2+2+1+1=10$ unterschiedliche Würfelfärbungen.

Ergebnis:

72

Im Trapez $\mathit{AXY}D$ ist $E$ der Mittelpunkt der Seite $\mathit{XY}$. Wenn man den Lotfußpunkt von $E$ auf $\mathit{AD}$ mit $E^{\prime }$ bezeichnet, so ist $E{E}^{\prime }$ Mittellinie im Trapez $\mathit{AXY}D$. Also ist die gesuchte Fläche $\overline{\mathit{AD}}\cdot \overline{E{E}^{\prime }}=72$.

Ergebnis:

1028

Für alle geraden Zahlen $a=2k$ mit $1\le k\le 1006$ ist $a^a={(2k)}^{2k}={({(2k)}^k)}^2$ eine Quadratzahl. Für ungerade Zahlen ist $a^a$ nur dann eine Quadratzahl, wenn $a$ selbst eine Quadratzahl ist. Wegen $44^2<2012<45^2$ kommen von den ungeraden Zahlen noch $22$ Quadratzahlen dazu, so dass es insgesamt $1006+22=1028$ solche $a$ gibt.

Ergebnis:

$\frac{2}{3}\cdot 2\pi =\frac{4}{3}\pi$

Der Weg der roten Ecke beschreibt zwei Kreisbögen, jeweils mit einem $\frac{1}{3}$ einer vollen Umdrehung eines Kreises. Einmal bleibt die Ecke an der Stelle, wo sie gerade ist, wenn um diese Ecke gedreht wird. Also ist der Gesamtweg $(\frac{1}{3}+\frac{1}{3})\cdot 2\pi =\frac{4}{3}\pi$.

Ergebnis:

$11111111100$

Aufgrund der Teilbarkeit durch $25$ muss die Zahl zwei Nullen am Ende haben. Außerdem muss sie druch $9(225=9\cdot 25)$ teilbar sein und aufgrund der Quersummenregel für die Teilbarkeit durch $9$ muss die Anzahl der Ziffern $1$ durch $9$ teilbar sein. Die kleinste Zahl mit diesen Eigenschaften ist $11111111100$.

Ergebnis:

28

Bill’s Alter $a$ ist das arithmetische Mittel der natürlichen Zahl $a-x$ und deren Quadrat $a+x$. Deshalb sind alle möglichen Werte für $a$ die Zahlen $\frac{1}{2}(6+36)=21$, $\frac{1}{2}(7+49)=28$, $\frac{1}{2}(8+64)=36$, $\frac{1}{2}(9+81)=45$, $\frac{1}{2}(10+100)=55$ und $\frac{1}{2}(11+121)=66$. Die einzige Quadratzahl darunter ist $36$, also ist $x=36-8=8^2-36=28$.

Anmerkung: Der Ansatz $v+x={(v-x)}^2$ liefert eine quadratische Gleichung in $v$ mit den Lösungen

Über die Ganzzahligkeitsbedingung und die Tatsache, dass $v$ eine Quadratzahl ist, erhält man ebenfalls $v=36$ und $x=28$.

Ergebnis:

$\sqrt{3}:3=1:\sqrt{3}$ oder umgekehrt.

Damit die zwei Ecken zusammenfallen, muss man an einer Geraden falten, die durch den Mittelpunkt des Rechtecks geht und auf einer Diagonalen senkrecht steht. Das entstehende Fünfeck besteht aus zwei kongruenten rechtwinkligen Dreiecken und einem gleichschenkligen Dreieck dazwischen. Die Diagonale teilt dieses gleichschenklige Dreieck in zwei kongruente rechtwinklige Dreiecke. Betrachtet man die vorausgesetzten Verhältnisse der Flächen, so sieht man, dass alle vier Dreiecke kongruent sind. Also ist der Winkel an der gemeinsamen Ecke $\frac{1}{3}\cdot 90^{\circ }=30^{\circ }$. Deshalb ist das mittlere Dreieck sogar gleichseitig. Aus dem Verhältnis aus Höhe und Seite im gleichseitigen Dreieck erhält man das Verhältnis

wobei mit $x$ die Seite des gleichseitigen Dreiecks bezeichnet wurde.

Ergebnis:

16

Da die Zahl durch $2$ teilbar sein muss, muss sie auf $6$ oder $8$ enden. Da sie auch durch $3$ teilbar sein muss, gilt dies auch für die Quersumme. Das bedeutet, dass die Summe der ersten beiden Ziffern Rest $1$ lässt, falls die letzte Ziffer $8$ ist, und Rest $0$, wenn die letzte Ziffer $6$ ist. Rest $1$ kann erreicht werden durch die Summe von Zahlen mit den Resten $2+2$ oder $3+1$. Da die Reihenfolge der Ziffern eine Rolle spielt, gibt es also $4+4=8$ Möglichkeiten. Analog kann der Rest $0$ durch $0+0$ bzw. $2+1$ erhalten werden, was wiederum $4+4=8$ Kombinationen ergibt. Insgesamt gibt es also $16$ Zahlen, die die Bedingung der Aufgabenstellung erfüllen.

Zweite Lösung: Systematisches Probieren ergibt

und wegen der erforderlichen Teilbarkeit durch 3 erhalten wir diejenigen, die mit $8$ bzw. $9$ starten, durch Addition von $300$ aus denen, die mit $5$ bzw. $6$ starten. Also gibt es $3+3+4+3+3=16$ Möglichkeiten.

Ergebnis:

$1+\frac{2}{\sqrt{3}}=1+\frac{2\sqrt{3}}{3}$

Mit $A$, $B$, $C$ werden die Mittelpunkte der kleinen Kreise bezeichnet und mit $S$ der des großen. $A$, $B$, $C$ sind Ecken eines gleichseitigen Dreiecks der Länge $2$. Die Höhen schneiden sich in $S$ und haben die Länge $\sqrt{2^2-1}=\sqrt{3}$. In einem gleichseitigen Dreieck sind die Höhen auch zugleich Seitenhalbierende. Deshalb ist $\overline{\mathit{AS}}=\frac{2}{3}\cdot \sqrt{3}$. Der Radius des Kreises $k$ ist also $1+\frac{2\sqrt{3}}{3}$.

Ergebnis:

6

Sei $n=10x+y$ für eine nicht negative ganze Zahl $x$ und eine Ziffer $y$. Dann ist $n^2=100x^2+20\mathit{xy}+y^2$. Die Zehnerstelle ist genau dann ungerade, wenn die Zehnerstelle von $y^2$ ungerade ist. Dies ist nur für $16$ und $36$ der Fall, so dass die Endziffer von $n^2$ nur $6$ sein kann.

Zweite Lösung: Für jede Quadratzahl $n^2$ gelten die folgenden beiden Gleichungen:

Wenn die Zehnerstelle $7$ ist, so erfüllen nur Zahlen, die auf $76$ enden, beide Bedingungen.

Ergebnis:

19

Folgende $19$-Kette ist ein Palindrom:

Wir zeigen, dass $19$ der kleinste mögliche Wert für $n$ ist. Nur eine Ziffer kann in einer $n$-Kette, die ein Palindrom ist, mit einer ungeraden Anzahl vorkommen, nämlich die mittlere. Für $n\le 9$ kann diese Bedingung offensichtlich nicht erfüllt werden. Für $10\le n\le 18$ kommen die Ziffern $0$ und $9$ jeweils genau einmal vor, so dass eine $n$-Kette kein Palindrom sein kann.

Ergebnis:

$(4,6,2)$

Addiert man alle drei Gleichungen, so erhält man

da $x$, $y$, $z$ positive Zahlen sind. Rücksubstitution ergibt die Gleichungen $(12-z)=10$, $(12-x)=8$ und $(12-y)=6$, woraus leicht die Lösung $(4,6,2)$ folgt.

Ergebnis:

0

Zeichne zwei Sehnen, die punktsymmetrisch zu den bereits vorhandenen bzgl. des Kreismittelpunktes liegen. Wenn nun die zwei Flächen gleich groß sein sollen, so muss mindestens eine Sehne durch den Mittelpunkt gehen.

Der maximale Abstand der längeren Sehne vom Kreismittelpunkt ist also $0$.

Ergebnis:

16

Der Wachmann muss um das erste Gebäude entweder am Anfang oder ganz am Schluß seines Wachganges gehen (in einer der beiden möglichen Richtungen), was vier Möglichkeiten ergibt. Für jedes der beiden verbleibenen Gebäude kann er unabhängig voneinander entscheiden, ob er es im Uhrzeigersinn oder im Gegenuhrzeigersinn umrundet. Diese Entscheidungen legen die Route eindeutig fest, so dass $4\cdot 2\cdot 2=16$ die gesuchte Lösung ist.

Ergebnis:

$\frac{21}{2}$

Eine Parallele zur kürzeren Seite durch eine weitere Ecke des Trapezes teilt dieses in ein Parallelogramm und ein Dreieck mit den Seiten $3$, $5-2=3$ und $3\sqrt{2}$, welches deshalb gleichschenklig und rechtwinklig ist. Die Fläche ist deshalb einfach $\frac{1}{2}\cdot 3\cdot 3+3\cdot 2=\frac{21}{2}$.

Ergebnis:

$\frac{42\cdot 41}{2}=21\cdot 41=861$

Sei $H$ die Anzahl der (nicht unbedingt direkt benachbarten) Paare, für die die größere Person hinter der kleineren steht. $H$ kann in einem Zug höchstens um 1 verringert werden. Wenn $H>0$ ist, dann gibt es einen Zug, der $H$ verringert. Bei $n$ Personen ist $H$ am Anfang höchstens $1+2+\cdots +(n-1)=n(n-1)∕2$, wenn die Leute genau entgegengesetzt zur geforderten Ordnung stehen. Also braucht man für die gewünschte Anordnung höchstens $42\cdot 41∕2=861$ Züge.

Ergebnis:

59

Wenn er einen Preis bezahlen kann, dann kann er auch diesen Preis plus ein Vielfaches von $7$ bezahlen. Also ist es ausreichend, die Vielfachen von $11$ und ihre Reste $mod7$ zu untersuchen. Es ist $0mod7=0$, $11mod7=4$, $22mod7=8$, $33mod7=5$, $44mod7=2$, $55mod7=6$ und $66mod7=3$. Ab $66$ kann er alle Beträge bezahlen, da sich ab dann die Reste wiederholen. Also ist $66-7=59$ der größte Preis, den er nicht bezahlen kann.

Allgemein: Haben die Münzen die teilerfremden Werte $p$ und $q$, so ist $(p-1)\cdot (q-1)-1$ der höchste Preis, der nicht mit diesen Münzen bezahlt werden kann.

Ergebnis:

$\pi$

Dasjenige geometrische Objekt, das bei gegebener Fläche den kleinsten Umfang hat, ist ein Kreis. Also muss man nur noch den Kreis in vier gleich große Teile aufteilen, wobei ein Teil wieder ein Kreis mit einem Viertel der ursprünglichen Fläche ist: Also entstehen ein Kreis mit dem halben Radius des gegebenen und drei andere Teile mit gleicher Fläche.

Deshalb ist $\pi$ der gesuchte Umfang.

Ergebnis:

$-2$

Sei $x$ eine gemeinsame Lösung. Subtraktion der beiden Gleichungen ergibt $(a-1)(x-1)=0$. Also ist $x=1$ oder $a=1$. Falls $x=1$ ist, ist $a=-2$. Im anderen Fall haben die Gleichungen keine reelle Lösung.

Ergebnis:

0

Sei $m$ eine Zahl, die man nach dem Streichen der ersten Ziffer erhält, und sei $c$ die gestrichene Ziffer. Die ursprüngliche Zahl ist dann $c\cdot 10^7+m$ und es muss die Gleichung $m=\frac{1}{35}(c\cdot 10^7+m)$ gelten. Diese kann vereinfacht werden zu $17m=c\cdot 2^6\cdot 5^7$. Nun ist aber die linke Seite durch $17$ teilbar und die rechte nicht, da $c$ eine Ziffer mit $c\le 9$ ist. Also gibt es keine solchen Zahlen.

Ergebnis:

$1006\cdot (1006^2-1)=1018107210$

Damit die Fläche maximal wird, muss die Seite der Länge $2012$ eine Kathete sein. Der Satz des Pythagoras ergibt $b^2+2012^2=c^2⟺2012^2=c^2-b^2=(c+b)(c-b)$. Die Fläche ist maximal, wenn $2012\cdot b∕2$ maximal ist. Dies wiederum ist der Fall, wenn die Differenz zwischen Hypotenuse und Kathete $b$ minimal ist. Wählt man $c=b+1$, so passen in obiger Gleichung die Paritäten nicht. Wählt man $c=b+2$, so erhalten wir eine einfache Gleichung für $b$:

Deshalb ist die maximale Fläche $1006\cdot (1006^2-1)$.

Ergebnis:

$\sqrt{10}$

Wir untersuchen verschiedene Umkreisradien. Für $1$, $\sqrt{2}$, $2$ und $2\sqrt{2}$ fällt jeweils eine Ecke mit dem Höhenschnittpunkt zusammen. Für $\sqrt{5}$ und $\sqrt{10}$ kann man die gewünschten Dreiecke konstruieren. Deshalb ist $\sqrt{10}$ der gesuchte Wert.

Ergebnis:

14

Wiederholte Anwendung von $a^2-b^2=(a-b)(a+b)$ ergibt $7^{2048}-1=(7-1)(7+1)(7^2+1)(7^4+1)\dots (7^{1024}+1)$. Bis auf $(7+1)$ sind alle Faktoren des Produkts genau einmal durch $2$ teilbar, da $7^{2n}+1\equiv 2\mathit{mod}4$ für $n\ge 1$. Also ist $14$ die gesuchte Lösung.

Ergebnis:

$98764312$

Die größte Zahl mit von Null verschiedenen, unterschiedlichen Ziffern ist $987654321$. Diese hat aber nur Persistenz $2$, da die $5$ und gerade Zahlen vorkommen, so dass man im zweiten Schritt $0$ erhält. Wir streichen die $5$ und vertauschen die letzten beiden Ziffern, um eine gerade Zahl zu erhalten. Dann ist $9\cdot 8\cdot 7\cdot 6\cdot 4\cdot 3\cdot 1\cdot 2=72576$, $7\cdot 2\cdot 5\cdot 7\cdot 6=2940$ und $2\cdot 9\cdot 4\cdot 0=0$ und somit die Aufgabe gelöst.

Ergebnis:

$1:4$

Betrachtet man ein Viereck, bei dem die Ecken $C$ und $D$ zusammenfallen, so ist $\mathit{GM}$ Mittellinie im Dreieck $\mathit{ABC}$ und das Verhältnis ist offensichtlich $\frac{1}{4}$.

Ergebnis:

270

Angenommen, wir betrachten den Würfel von oben. In Tiefe $0$ (also auf der oberen Seitenfläche des Würfels) sind es $21$ cm${}^2$, in Tiefe $2$ cm und $4$ cm jeweils $12$ cm${}^2$. Die Situation ist in alle sechs Richtungen die gleiche und man erhält insgesamt $(21+2\cdot 12)\cdot 6c{m}^2=270c{m}^2$.

Ergebnis:

$1+\sqrt{2}$

Zu jeder Trajektorie gibt es eine Trajektorie gleicher Länge, die zuerst nur nach rechts geht und dann nur nach oben. Es genügt also solche Trajektorien zu betrachten. Die längste Trajektorie muss sicherlich durch den Mittelpunkt gehen. Wir bezeichnen mit $a$ die Strecke, die man vom Mittelpunkt aus nach rechts geht, und mit $b$ diejenige, die man nach oben geht. Da der längste Weg an der Kreislinie enden wird, gilt $a^2+b^2=1$, wobei wir $a+b$ maximieren müssen. Dies ist gleichbedeutend mit der Maximierung von ${(a+b)}^2=a^2+b^2+2\mathit{ab}=1+2\mathit{ab}$. Wegen der Ungelichung $0\le {(a-b)}^2=a^2-2\mathit{ab}+b^2$ ergibt sich $2\mathit{ab}\le a^2+b^2=1$. Gleichheit erhält man für $a=b$, woraus $a=b=\sqrt{1∕2}=\frac{\sqrt{2}}{2}$ folgt. Addiert man noch den Abstand vom äußersten linken Punkt zum Mittelpunkt, so erhält man das Ergebnis $1+\sqrt{2}$.

Ergebnis:

$5\cdot 5\cdot 7\cdot 7\cdot 11\cdot 13=175175$

Der Rest eines Produktes ist gleich dem Produkt der Reste der einzelnen Faktoren, z.B. $7!mod6=1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 0\cdot 1=0$. Um Rest $5$ zu erhalten, darf die Zahl weder durch $2$ noch durch $3$ teilbar sein, d.h. man muss alle Faktoren $2$ und $3$ von $15!$ ausschließen. Danach bleibt die Zahl $5^3\cdot 7^2\cdot 11\cdot 13$, die aber Rest $1$ ergibt. Jeder Faktor ergibt entweder Rest $1$ oder $5mod6$, so dass man noch einen mit Rest $5$ eliminieren muss. Der kleinste davon ist $5$. Also ist das Ergebnis $5\cdot 5\cdot 7\cdot 7\cdot 11\cdot 13=175175$.

Ergebnis:

49

Man teilt die Geraden in drei Fälle auf: Solche, die durch den Mittelpunkt des Würfels gehen $(9+8∕2=13)$, solche, die durch den Mittelpunkt der Seitenfläche, aber nicht durch den Mittelpunkt des Würfels gehen ($4$ auf jeder Seitenfläche) und solche, die entlang einer Kante verlaufen ($12$). Dies ergibt insgesamt $13+24+12=49$.

Ergebnis:

$1+3+12+25=41$

Es ist klar, dass $n<26$ sein muss. An jedem Tag werden $\frac{n(n+1)}{2}$ Punkte vergeben, insgesamt also $k\cdot \frac{n(n+1)}{2}$. Diese Summe muss aber gleich $26\cdot n$ sein. Gleichsetzen ergibt $k(n+1)=52=2\cdot 2\cdot 13$. Durch Probieren findet man, dass es für $k\in \{2,4,13,26\}$ eine mögliche Punkteverteilung gibt und für $k\in \{1,52\}$ nicht. Die Summe aller möglichen $n$ ist dann $(26-1)+(13-1)+(4-1)+(2-1)=41$.

Ergebnis:

26

Der Einfachheit halber betrachtet man einen dreidimensionalen Raum, der von Ebenen geschnitten wird. Wenn der Raum irgendwie zerschnitten ist, dann kommen durch die nächste Ebene so viele neue Teile hinzu wie sie durchschnitten hat. Man betrachtet also die Schnittgeraden der alten Ebenen mit der neuen. Die Anzahl der neuen Teile ist gleich der Anzahl Teile, in die die Geraden die neue Ebene zerlegen. Deshalb ist $v_n=v_{n-1}+p_{n-1}$, wobei $v_n$ das Ergebnis für $n$ Schnitte ist und $p_n$ die Anzahl der neuen Teile, in die wir eine Ebene durch $n$ Geraden zerlegen können. Durch einfaches Zeichnen auf Papier kann man die maximalen Werte für $p_1$, $p_2$, $p_3$ und $p_4$ finden. Sie lauten $2$, $4$, $7$ und $11$. Mit $v_1=2$ erhalten wir das Ergebnis $2+2+4+7+11=26$.

Hinweis: Allgemein lautet die Formel

Ergebnis:

$\sqrt{2}$

Man hat zwei Arten von Volumenkörper vorliegen: Ein reguläres Tetraeder der Seitenlänge $1$ und eine vierseitige Pyramide, bei der ebenfalls alle Seiten die Länge $1$ haben. Die Grundfläche der Pyramide ist $1$ und die Höhe erhält man mit dem Satz des Pythagoras als

so dass das Volumen also $\frac{1}{3\cdot \sqrt{2}}$ ist. Die Grundfläche eines Tetraeders (gleichseitiges Dreieck) ist $\frac{\sqrt{3}}{4}$ und die Höhe

so dass sich das Volumen zu $\frac{\sqrt{2}}{3\cdot 4}$ ergibt. Durch Aufsummieren erhält man $2\cdot \frac{\sqrt{2}}{6}+8\cdot \frac{\sqrt{2}}{12}=\sqrt{2}$.

Ergebnis:

$3∕5$

Die Wahrscheinlichkeit, dass er in den nächsten $20$ Minuten kein Auto sieht, ist $1-\frac{609}{625}=\frac{16}{625}$. Wenn die Wahrscheinlichkeit, dass er in den nächsten $5$ Minuten kein Auto sieht, $p$ ist, dann ist sie für $20$ Minuten $p^4$. Also ist $p=\frac{2}{5}$ und die Wahrscheinlichkeit ein Auto zu sehen ist dann $1-\frac{2}{5}=\frac{3}{5}$.

Ergebnis:

$2∕3\cdot 8∕9\cdot 26∕27=\frac{2^5\cdot 13}{3^6}$

Für jeden Fehler bestimmt man die Wahrscheinlichkeit dafür, dass er am Ende nicht mehr da ist. Die Wahrscheinlichkeit, dass ein Fehler $k$ Tage lang da ist, beträgt ${(\frac{1}{3})}^k$, und die Wahrscheinlichkeit, dass er nach $k$ Tagen nicht mehr da ist, ist dann $1-{(\frac{1}{3})}^k$. Die Ereignisse, einen einzelnen Fehler nicht zu entdecken, sind unabhängig. Deshalb dürfen wir multiplizieren:

Ergebnis:

168

Sei $R$ die Anzahl der roten Karten, $B$ die Anzahl der blauen Karten und $G$ die Anzahl der gelben Karten. Jede rote Karte trägt $1+2B$ zum Gesamtergebnis bei, nämlich $1$ für sich selbst und $2$ für jede blaue Karte. Jede gelbe Karte trägt $3\cdot B\cdot G$ zum Gesamtergebnis bei. Insgesamt lassen sich also

Punkte erzielen.

Ist $B=0$, so ist das maximale Ergebnis $15$. Ist $B=1$, so ist das Ergebnis immer

Ist $B>1$, so ist es besser alle roten Karten durch gelbe zu ersetzen. Also ist es in diesem Fall sinnvoll $R=0$ zu wählen, so dass für $B>1$ das Gesamtergebnis dann $3\cdot B\cdot G$ ist. Dann ist aber $B+G=15$, weshalb das Maximum für $B=7$ und $G=8$ erreicht wird, was das Gesamtergebnis $168$ ergibt.

Ergebnis:

$\frac{19}{40}$

Zunächst erkennt man, dass beide Würfel eine symmetrische Verteilung haben, d.h. die Wahrscheinlichkeit beim $20$-seitigen Würfel $x$ zu erhalten ist gleich der Wahrscheinlichkeit $21-x$ für $1\le x\le 20$ zu erhalten. Analog ist die Wahrscheinlichkeit, bei den drei sechsseitigen Würfeln $y$ zu erhalten, gleich der Wahrscheinlichkeit $21-y$ für $3\le y\le 18$ zu bekommen. Auf gleiche Weise kann man schließen, dass beide mit der gleichen Wahrscheinlichkeit gewinnen. Deshalb ist die gesuchte Antwort $\frac{1-p}{2}$, wobei $p$ die Wahrscheinlichkeit eines Unentschiedens ist. Und diese ist $\frac{1}{20}$, denn was immer Christian würfelt, Matthias hat immer die Wahrscheinlichkeit $\frac{1}{20}$, das gleiche zu würfeln. Also ist die gesuchte Wahrscheinlichkeit $\frac{19}{40}$.

Ergebnis:

$10\times 10!\cdot 10!=2^{17}\cdot 3^8\cdot 5^5\cdot 7^2$

Auf jedem Weg sammelt der Reisende jede der Zahlen $2,3,\dots ,9$ mindestens zweimal, einmal für die Spalte und einmal für die Zeile. Außerdem gibt es für jedes $i$ außer $1$ und $10$ einen Weg, der die $i$-te Zeile und die $i$-te Spalte genau einmal kreuzt. Deshalb können $2,3,\dots ,9$ jeweils nur genau zweimal im Resultat vorkommen. In jeder Reisezahl muss 10 mindestens dreimal vorkommen (der Reisende muss das Feld rechts unten betreten und vom vorherigen sammelt er ebenfalls eine 10). Es ist leicht zu sehen, dass es einen Weg gibt, der nur dreimal 10 enthält. Deshalb ist das gesuchte Ergebnis $10\times 10!\cdot 10!=2^{17}\cdot 3^8\cdot 5^5\cdot 7^2$.

Ergebnis:

$\frac{72}{\sqrt{15}}=\frac{24\sqrt{15}}{5}$

Aufgrund der Flächenformel $A=\frac{g\cdot h}{2}$ kann man schließen, dass das gegebene Dreieck ähnlich ist zu einem Dreieck mit den Seiten $2$, $3$ und $4$. Das Dreieck habe also die Seitenlängen $2a$, $3a$ und $4a$ und somit die Fläche $A=\frac{2a\cdot 6}{2}=6a$. Benutzt man die Formel von Heron zur Berechnung der Fläche, so folgt

mit $s=\frac{2a+3a+4a}{2}=\frac{9a}{2}$, also

Gleichsetzen ergibt

also $a=\frac{24}{\sqrt{135}}$. Der Umfang ist dann $9a=\frac{72}{\sqrt{15}}$.

Ergebnis:

$1999\cdot 2000=3998000$

Sei

dann ist $s=\sqrt{n+s}$. Löst man die entsprechende quadratische Gleichung in $s$, so erhält man

und da $s$ rational sein soll, gibt es eine rationale Zahl $a$ mit $1+4n=a^2$. Hieraus erhält man leicht $n=\frac{1}{4}(a^2-1)$. Da $n\in \mathbb{N}$ ist, muss auch $a\in \mathbb{N}$ gelten (wäre $a=p∕q$ mit teilerfremden $p$ und $q$, $q\ne 1$, so wäre $n=(p^2-q^2)∕4q^2$ und $q$ müßte $p$ teilen, was einen Widerspruch ergibt). Wegen $n=\frac{a-1}{2}\cdot \frac{a+1}{2}$ muss $a$ ungerade sein. Außerdem folgt aus $n\le 4000000$, dass $\frac{a+1}{2}=2000$ sein muss. Also ist $n=1999\cdot 2000$ die gesuchte Lösung.

Ergebnis:

$24\cdot 7=168$

Als erstes wählt man für die Fliese in der Mitte die Zahlen $1$, $2$ und $3$, $4$. Die Koordinaten des Quadrats links oben seien $(1,1)$. Mit $A$ und $B$ werden die beiden Zahlen bezeichnet, die die Koordinaten $(4,1)$ und $(4,6)$ haben. Also muss $A\in \{3,4\}$ und $B\in \{1,2\}$ gelten. Wenn das Paar $(A,B)$ eines der Tupel $(3,2)$, $(4,1)$, $(3,1)$ ist, dann gibt es genau eine Möglichkeit den Rest des Maxi-Quadrats zu füllen. Im Fall $(A,B)=(4,2)$ gibt es vier Möglichkeiten. Da es $4!=24$ mögliche Fliesen in der Mitte gibt, ist das Ergebnis $24\cdot 7=168$.

Ergebnis:

1010309

Aus der Tatsache, dass der Nachfolger von Ballon durch $210=2\cdot 3\cdot 5\cdot 7$ teilbar ist, folgt sofort, dass die letzte Ziffer von Ballon $9$ sein muss. Die Quersumme von Ballon muss die Form $3k+2$ haben wegen $210-1\equiv 2\mathit{mod}3$. Aufgrund der ersten Voraussetzung ist die Quersumme gerade. Also ist sie von der Form $3k+2$, gerade, größer als $9$ und höchstens $24$. Also kommen als Quersumme nur noch $14$ und $20$ in Frage, was $7$ bzw. $10$ Ziffern entspricht. Da sich gerade und ungerade Ziffern abwechseln, sind die kleinsten Lösungen $1010109$ und $2101010109$ mit den Quersummen $12$ und $15$, wenn man die Teilbarkeit durch $7$ und den Rest $2$ beim Teilen durch $3$ unberücksichtigt lässt. Die Quersumme im zweiten Fall ist ungerade, weshalb eine Quersumme $20$ nicht erreicht werden kann. Im ersten Fall müssen wir die Quersumme um $2$ vergrößern, also eine Ziffer um $2$ erhöhen. Nun prüft man leicht, dass $1010309$ die einzige Lösung ist, indem man die Teilbarkeitsbedingung für $7$ (und $3$) wieder berücksichtigt.

Ergebnis:

9376

Es muss $n^2-n=n(n-1)=10000x$ für eine natürliche Zahl $x$ gelten. Selbstverständlich sind $n$ und $n-1$ teilerfremd. Da $5^4$ die rechte Seite teilt, muss es auch die linke Seite teilen. Also teilt $5^4=625$ entweder $n$ oder $n-1$. Analog teilt $2^4=16$ entweder $n$ oder $n-1$. Also ist $n=625k+b$ mit $k\in \{1,2,\dots ,15\}$ und $b\in \{0,1\}$. Nun lässt $625$ beim Teilen durch $16$ Rest $1$, also $n$ beim Teilen durch $16$ Rest $k+b$. Also muss $k+b\in \{0,1,16\}$ gelten. Die Zahl $n$ ist nur für $(k,b)=(15,1)$ vierstellig, nämlich $n=9376$, und man kann leicht überprüfen, dass $n$ alle Bedingungen erfüllt.

Ergebnis:

$900\cdot 55000=49500000$.

Man kann eine bijektive Zuordnung zwischen fünfstelligen Palindromen und dreistelligen Zahlen herstellen. Zur Zahl $\mathit{abc}$ gehört das Palindrom $\mathit{abcba}$ für eine Ziffer $a\ne 0$ und beliebigen Ziffern $b$ und $c$. Die Summe aller Palindrome kann nun ziffernweise berechnet werden: Jedes $a$ addiert $a\cdot 10001$, jedes $b$ addiert $b\cdot 1010$ und jedes $c$ addiert $c\cdot 100$ zu der Summe. Jeder mögliche Wert für $a$ kommt $100$-mal in der Summe vor, jeder mögliche Wert von $b$ bzw. $c$ $90$-mal. Die Gesamtsumme ist also

Ergebnis:

$\left(\genfrac{}{}{0.0pt}{}{50}{3}\right)=19600$

Zunächst formuliert man das Problem neu, um die Bedingung, dass $a$, $b$, $c$, $d$ ungerade sein müssen, zu eliminieren. Sei $a=2A+1$ und die restlichen Zahlen $b$, $c$, $d$ analog ersetzt. Dann gibt es eine bijektive Zuordnung zwischen den Quadrupeln $(a,b,c,d)$ ungerader positiver Zahlen, die $a+b+c+d=98$ erfüllen, und den Quadrupeln $(A,B,C,D)$ natürlicher Zahlen, die $A+B+C+D=\frac{1}{2}(98-4)=47$ erfüllen. Der Rest ist eine Standardübung in Kombinationen mit Wiederholungen. Das Ergebnis ist $\left(\genfrac{}{}{0.0pt}{}{50}{3}\right)=19600$ (jedes Quadrupel $(A,B,C,D)$ gehört zu einer Folge von $47$ Bällen und $3$ Trennlinien).

Ergebnis:

$(10^{11}+1)\cdot 16∕121=16\cdot 826446281=13223140496$

Sei $n$ die gesuchte Zahl. Für die Zahl $N$, die durch zweimaliges Hintereinanderschreiben von $n$ entsteht, gilt $N=n(10^{11}+1)=n\cdot 11^2\cdot D$ für eine natürliche Zahl $D$. Die Zahl $D$ lässt sich berechnen aus

Aufgrund der zweiten Bedingung kann $n$ geschrieben werden als $n=t^2\cdot D$. Also ist $N={(11\cdot t\cdot D)}^2$. Nun muss $t$ nur noch so gewählt werden, dass $n$ elfstellig ist und mit der Ziffer $1$ beginnt. Nur $t=4$ erfüllt diese Bedingung und $16\cdot 826446281=13223140496$.

Ergebnis:

132

Sei $\mathit{ABC}$ eines der beiden Dreiecke mit $\overline{\mathit{AC}}=24$ und $\overline{\mathit{BC}}=18$. Ferner sei $I$ der Inkreismittelpunkt und $O$ der Umkreismittelpunkt von $\mathit{ABC}$. Wegen $(18,24,30)=6\cdot (3,4,5)$ ist $\mathit{\angle ACB}$ ein rechter Winkel und für die Radien $r$ und $R$ des In- und Umkreises von $\mathit{ABC}$ gilt $r=\frac{1}{2}(18+24-30)=6$ und $R=\frac{1}{2}\cdot 30=15$. Es gibt nur einen Durchmesser $A^{\prime }{B}^{\prime }$ des Umkreises von $\mathit{ABC}$, der von $\mathit{AB}$ verschieden ist und den Inkreis von $\mathit{ABC}$ berührt; er muss sysmmetrisch zur Geraden $\mathit{IO}$ liegen. $A^{\prime }{B}^{\prime }$ ergibt sich also auch als Mittelsenkrechte von $\overline{\mathit{AC}}$. Die Mittelsenkrechte geht natürlich durch $O$ und da ihr Abstand von $\mathit{BC}$ genau $12$ ist, ist ihr Abstand von $I$ gleich sechs. Das zweite Dreieck $A^{\prime }{B}^{\prime }{C}^{\prime }$ ist also symmetrisch zu $\mathit{ABC}$ bzgl. $\mathit{OI}$ und $A^{\prime }{B}^{\prime }\perp \mathit{AC}$ und $A^{\prime }{C}^{\prime }\perp \mathit{AB}$. Schließlich kann der Überlappungsbereich der zwei Dreiecke dadurch berechnet werden, dass man von der Fläche von $\mathrm{\Delta }\mathit{ABC}$ die Flächen der drei kleineren Dreiecke, die zu $\mathrm{\Delta }\mathit{ABC}$ ähnlich sind, abzieht; ihre Seitenlängen sind $9,12,15$ (Dreieck bei $A$), $6,8,10$ (Dreieck bei $B$) und $3,4,5$ (Dreieck bei $C$). Also ist die gesuchte Fläche

Ergebnis:

2040

Man färbt die $10$ schwarzen Zellen der Reihe nach ein. Die Zellen werden analog zu einem Schachbrett mit $A1\dots E5$ bezeichnet. O.B.d.A. werden $A1$, $B1$ (aus Symmetriegründen muss dann das Ergebnis mit $\left(\genfrac{}{}{0.0pt}{}{5}{2}\right)=10$ multipliziert werden) und zusätzlich $B2$ (Multiplikation mit $4$) gefärbt. Wenn nun $A2$ in der zweiten Zeile gefärbt wird, so muss ein restliches $3\times 3$-Gitter den Vorgaben entsprechend gefärbt werden, wofür es $6$ Möglichkeiten gibt. Falls eine andere Zelle in der zweiten Zeile gefärbt wird, so sei dies o.B.d.A. $C2$ (Multiplikation mit 3) und in der dritten Zeile $C3$ (wieder Multiplikation mit 3). Wenn nun $A3$ gefärbt wird, so gibt es nur noch eine Möglichkeit ($D4$, $D5$, $E4$, $E5$) gemäß den Regeln einzufärben. Andernfalls gibt es vier Möglichkeiten. Also gibt es insgesamt

Färbungen.

Ergebnis:

$\frac{\sqrt{6}+\sqrt{2}}{2}$

Sei $V$ der Wert, den man minimieren will. Falls $X=A$ und $Y=B$ ist, dann ist $V=2$ und es ist mit der Dreiecksungleichung einfach zu zeigen, dass $V\ge 2$, falls $X$ näher an genau $0$, $2$ oder $4$ Ecken ist als $Y$. Also kann man annehmen, dass die Entfernung von $A$ von $X$ aus gemessen wird und die Entfernung von $B$, $C$, $D$ von $Y$ aus. Man muss also den Wert $V=\mathit{AX}+\mathit{BY}+\mathit{CY}+\mathit{DY}$ minimieren. Es ist klar, dass $V$ nur dann minimal ist, wenn $X$ auf $A$ liegt und $Y$ der Fermatpunkt des Dreiecks $\mathit{BCD}$ ist, d.h. wenn alle Winkel $\mathit{BY}C$, $\mathit{CY}D$, $\mathit{DY}B$ genau $120$ Grad haben. (Diese notwendige Eigenschaft des Fermatpunktes erkennt man durch Drehung des Dreiecks $\mathit{BY}C$ um Punkt $B$ um $60$ Grad in ein Dreieck $B{Y}^{\prime }{C}^{\prime }$ und Betrachtung der Länge des Polygonzugs bestehend aus den Segmenten $\mathit{DY}$, $Y{Y}^{\prime }$, $Y^{\prime }{C}^{\prime }$ im Vergleich zur Strecke $D{C}^{\prime }$.) Eine einfache Rechnung ergibt nun $\mathit{\angle BDY}=\mathit{\angle Y}\mathit{BD}=30^{\circ }$ und der Satz des Pythagoras ergibt mit $\overline{\mathit{BD}}=\frac{\sqrt{2}}{2}$ die Längen $\overline{\mathit{DY}}=\overline{\mathit{BY}}=\frac{\sqrt{2}}{\sqrt{3}}$ und $\overline{\mathit{CY}}=\frac{\sqrt{2}}{2}-\frac{1}{2}\cdot \frac{\sqrt{2}}{\sqrt{3}}$. Also ist

Da $\frac{\sqrt{6}+\sqrt{2}}{2}<2$ gilt, ist es die gesuchte Lösung.

Ergebnis:

$1∕2012\cdot 1∕1025=1∕2062300$

Parkplatz $1$ kann nur dann als letzter genommen werden, wenn Parkplatz $2$ als erster genommen wird (mit der Wahrscheinlichkeit $\frac{1}{2012}$) und deshalb Parkplatz $2012$ direkt danach. Dann werden die Parkplätze $3$ bis $2011$ gefüllt, bis nur noch Abstände der Größen $1$ oder $2$ übrig bleiben. In diesem Augenblick ist die Wahrscheinlichkeit, dass Parkplatz $1$ als letzter genommen wird, der reziproke Wert aller noch freien Parkplätze, da jeder Parkplatz die gleiche Wahrscheinlichkeit hat als letzter genommen zu werden. Dabei ist zu beachten, dass man immer die gleiche Anzahl an Lücken der Größen $1$ oder $2$ enthält, wenn man nur auf die Größen der Lücken schaut und die Autos in der jeweils größten platziert werden. Also kann man ihre Anzahl eindeutig bestimmen. Sei $f(n)$ die Anzahl der freien Parkplätze, wenn Autos auf $n+2$ Plätzen in einer Reihe wie vorgeschrieben parken und der erste und der letzte Parkplatz bereits belegt sind. Das erste Auto parkt nun in der Mitte, was die Aufgabe auf die neuen Fälle $f(\lfloor \frac{n-1}{2}\rfloor )$ und $f(\lceil \frac{n-1}{2}\rceil )$ aufteilt. Also haben wir eine rekursive Beziehung $f(n)=f(\lfloor \frac{n-1}{2}\rfloor )+f(\lceil \frac{n-1}{2}\rceil )$ mit den Anfangsbedingungen $f(1)=1$ und $f(2)=2$. Durch Berechnen von $f(n)$ für kleine Werte von $n$ erhält man

und kann dann folgende geschlossene Darstellung herleiten:

Also ist $f(2009)=1024$ und die gesuchte Wahrscheinlichkeit ist $\frac{1}{2012}\cdot \frac{1}{1024+1}=\frac{1}{2062300}$.

Ergebnis:

$0,2,1\pm \sqrt{6},1\pm \sqrt{8}$

Wegen

erhält man nach der Substitution $x^2-2x=z$ die Gleichung