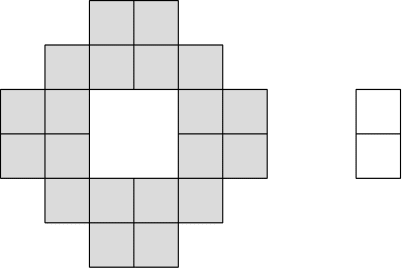
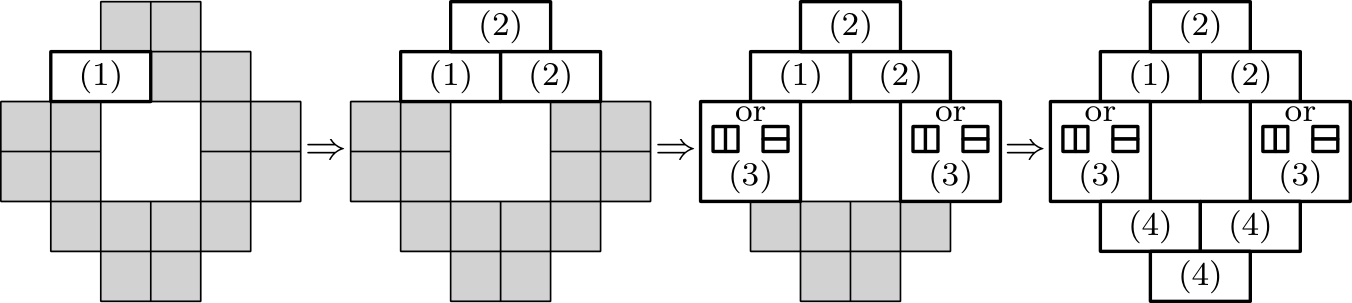
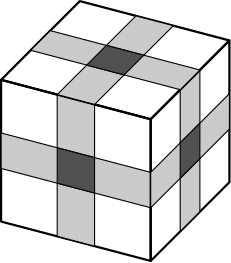
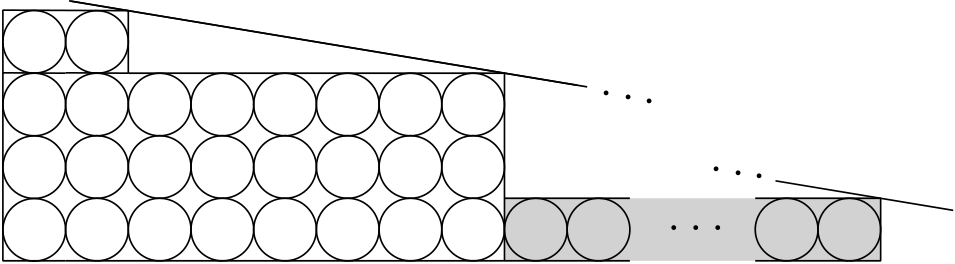
Ein Gebäude hat Etagen. Der Flur jeder Etage ist über jede von zwei Flurtüren zugänglich. In jedem Flur gibt es vier Zimmer, jedes Zimmer hat einen Bewohner und eine eigene Tür. An jeder Zimmer- bzw. Flurtüre wird jeweils ein Schloss angebracht. Es sollen Schlüssel verteilt werden, um Folgendes sicherzustellen:
- Jede Person hat Zugang zu ihrem eigenen Zimmer, aber nicht zu dem einer anderen Person.
- Jede Person hat Zugang zum Flur auf ihrer Etage.
- Es ist erlaubt, dass jemand Zugang zu Fluren in anderen Etagen hat.
Zu jedem Schloss gehört ein Schlüssel, der als Original oder als Kopie davon genau dieses Schloss und weitere Kopien davon schließt. Kopien eines verwendeten Schlosses können bei Bedarf in verschiedene Türen eingebaut werden, eine beliebige Anzahl an Kopien von Schlüsseln für dieses Schloss darf hergestellt und verteilt werden. Jede Person kann so viele Schlüssel ausgehändigt bekommen, wie sie benötigt. Das für die Installation verantwortliche Unternehmen ist bestrebt, die Gesamtkosten für die Herstellung der Schlüssel zu minimieren. Die Herstellung eines neuen Schlüssels kostet 3, die einer Kopie eines vorhandenen Schlüssels kostet 2. Wie hoch sind die minimalen Gesamtkosten für alle Schlüssel unter Einhaltung der oben genannten Bedingungen?Lösung
Ergebnis:
Um die Kosten zu minimieren, ist es billiger, wenn ein Bewohner einen einzigen Schlüssel hat, der sowohl sein Zimmer als auch eine Flurtür öffnet, als zwei separate Schlüssel zu haben, selbst wenn es nur Kopien wären. Dies bedeutet jedoch, dass dann eine Flurtür für andere unzugänglich bleiben muss, da der Zugang zu dieser Tür auch den Zugang zum Zimmer jenes Bewohners ermöglichen würde.
Somit reduziert sich das Problem auf die Minimierung der Schlüsselkosten für 160 Etagen, bei denen jeder Flur nur einen Eingang und drei separate Zimmer hat. Angenommen, es werden verschiedene Schlüsseltypen verwendet. Jeder Bewohner erhält einen Schlüssel für sein Zimmer und einen Schlüssel für den Flur. Diese beiden Schlüssel können nicht vom gleichen Typ sein. Wäre der Zimmerschlüssel eines Bewohners vom selben Typ wie der Flurschlüssel, würden die beiden anderen Bewohner, die sich den Flur teilen, Zugang zum Zimmer dieses Bewohners haben. Außerdem können keine zwei Bewohner das gleiche Schlüsselpaar haben, da dies bedeuten würde, dass sie Zugang zum gleichen Zimmer haben. Daher ist die Anzahl der möglichen Paare verschiedener Schlüsseltypen durch gegeben.
Da insgesamt Schlüsselpaare verteilt werden müssen, bestimmen wir die untere Grenze für aus der Ungleichung
zu . Wir zeigen nun, dass es möglich ist, genau verschiedene Schlüsseltypen zu verwenden. Dazu teilen wir die 160 Etagen in 32 Gruppen zu je 5 Etagen auf. Die Schlüsselzuweisungen sind wie folgt, wobei der erste Schlüssel des Paares für den Flur und der zweite für das Zimmer steht:
- Die 15 Bewohner der ersten Gruppe erhalten die Schlüsselpaare , , …, .
- Die zweite Gruppe erhält die Schlüsselpaare .
- Dieses Muster setzt sich fort, wobei die 18. Gruppe die Schlüsselpaare erhält.
- Dieses Muster setzt sich fort bis zur 31. Gruppe, welche die Schlüsselpaare erhält.
- Schließlich erhält die letzte, die 32. Gruppe die Schlüsselpaare , , …, .
Es ist leicht zu sehen, dass diese Verteilung die oben genannten Bedingungen erfüllt. Daher ist die minimale Anzahl der benötigten Schlüsseltypen, zu denen wir Originale und insgesamt Kopien erstellen müssen, um alle Schlüssel ausgeben zu können.
Unter Berücksichtigung der im ersten Absatz erwähnten Bewohner müssen insgesamt Schlüssel hergestellt und Kopien erstellt werden. Die endgültigen Kosten belaufen sich also auf .