Úloha 1
Pokud zvětšíme hranu krychle o , o kolik procent se zvětší její objem? Výsledek: Zvětšit hranu o znamená zdvojnásobit ji na . Objem původní krychle byl , po zvětšení bude . Zvětšil se o , což je .Řešení
Pokud zvětšíme hranu krychle o , o kolik procent se zvětší její objem? Výsledek: Zvětšit hranu o znamená zdvojnásobit ji na . Objem původní krychle byl , po zvětšení bude . Zvětšil se o , což je .Řešení
Na kolik nejvíce částí se dá třemi přímkami rozdělit mezikruží?

Výsledek:
9
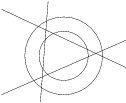
Chceme, aby všechny průsečíky přímek byly různé, ležely uvnitř mezikruží a aby každá přímka byla sečnou mezikruží. To se nám podaří, pokud bude vnitřní kružnice něco mezi vepsanou a opsanou kružnicí trojúhelníka, jejž ohraničují tři přímky.
je pěticiferné číslo dělitelné . Zjistěte hodnotu součinu . Výsledek: Číslo musí být dělitelné a (). Z kritéria dělitelnosti 8 dostáváme, že , z dělitelnosti 9 plyne , proto .Řešení
Učitel matematiky se rozhodl uspořádat dvě kola minináboje pětičlenných družstev ve své třídě. V prvním kole se žáci rozdělili do družstev tak, jak chtěli. Ve druhém kole je učitel rozdělil tak, aby nikdo nebyl v družstvu s tím, s kým už byl v družstvu v prvním kole. Jaký je nejmenší počet žáků, pro který se to učiteli vždy podaří? Výsledek: 25 Počet žáků musí být dělitelný 5. Pokud by jich bylo 20 nebo méně, tak z Dirichletova principu plyne, že alespoň dva žáci, kteří byli spolu v prvním kole, musí být spolu i ve druhém. 25 žáků už stačí, protože můžeme do každého nového družstva vzít jednoho z každého týmu.Řešení
Vanilkový koláč ve tvaru kvádru o rozměrech je na celém povrchu pokryt tenkou vrstvou čokolády. Koláč rozřežeme na kousky . Kolik procent kousků na sobě nemá žádnou čokoládu? Výsledek: Po snězení všech kousků s čokoládou nám zůstane kvádr složený ze všech kousků bez čokolády, kterých tedy musí být 192. Z celkového počtu kousků už lehce spočítáme procenta: .Řešení
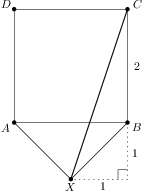
Mějme čtverec se stranou délky a bod ležící mimo něj tak, že platí . Jakou délku má nejdelší úhlopříčka pětiúhelníku ? Výsledek: Nejdelší je zřejmě úhlopříčka . Nechť je střed strany . Chceme získat délku . Trojúhelník je pravoúhlý rovnoramenný, takže je střed pomyslného čtverce ( a získáme překlopením přes ). Takže . Délku už spočítáme snadno z Pythagorovy věty: .Řešení
V součinu každou cifru zvětšete nebo zmenšete o 1 tak, aby byl výsledek správný. Jaký bude výsledek? Výsledek: 2012 Stačí vyzkoušet všechny možné změny levé strany (je jich 16) a zjistit, pro které vyjde číslo, které lze změnit na pravou stranu. Zkoušení si lze ulehčit například pozorováním, že výsledek musí začínat na dvojku, takže číslice na místě stovek ve druhém činiteli se musí změnit na 5 a první činitel na 4.Řešení
Pro celá čísla a platí, že jejich součet je nanejvýš a jejich rozdíl je menší než . Najděte maximální hodnotu, které může nabývat výraz .
Výraz má hodnotu nejmenšího čísla z dvojice , podobně má hodnotu největšího čísla z dvojice . Výsledek: 300 Bez újmy na obecnosti předpokládejme, že . Pak . Této hodnoty umíme dosáhnout pro .Řešení
Nechť , , jsou reálná čísla taková, že aritmetický průměr čísel a je roven a aritmetický průměr čísel a je roven . Jaký je aritmetický průměr čísel , a ? Výsledek: 5 Sečtením prvních dvou rovností pro aritmetický průměr dostáváme Správný výsledek dostaneme vydělením této rovnosti třemi.Řešení
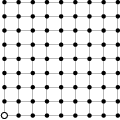
Ve čtvercové mřížce o devíti řadách a devíti sloupcích stojí 81 stromů s nulovou šířkou. Zahradník pokácel jeden z rohových stromů a teď se z jeho místa dívá na ostatní stromky. Některé však nevidí, protože je zakrývají jiné (strom je zakrytý právě tehdy, když na úsečce mezi stromem a zahradníkem leží další strom). Kolik stromů zahradník vidí?
Výsledek:
45
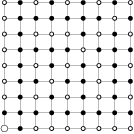
Nakreslíme si obrázek a postupně kontrolujeme stromy od těch, které jsou nejblíže k zahradníkovi, až po ty úplně nejvzdálenější. Kontrolovaný strom vždy označíme za viditelný, pokud ještě nebyl vyškrtnut, a následně vyškrtneme všechny další stromy, které tento strom zakrývá (leží spolu s ním a se zahradníkem na jedné přímce). Nakonec spočítáme všechny stromy, které jsme označili za viditelné.
Kolika způsoby lze stěny kostky obarvit černou a bílou barvou? Dvě obarvení považujeme za stejná, pokud se dokážeme otočením jednoho z nich dostat na druhé. Výsledek: Možnosti rozdělíme podle toho, kolik stěn obarvíme bílou barvou. Pro žádnou bílou stěnu máme jednu možnost, stejně tak pro jednu bílou stěnu. Pro dvě stěny jsou možnosti dvě: bílé stěny spolu buď sousedí, nebo jsou protilehlé. Pro tři stěny jsou opět dvě možnosti: buď mají společný vrchol, nebo jsou dvě protilehlé a třetí s oběma sousedí hranami. Pro čtyři je stejně možností jako pro dvě (místo čtyř bílých můžeme umisťovat dvě černé). Ze stejného důvodu je počet obarvení pro pět a šest po řadě stejné jako pro jednu a žádnou. Dohromady je tedy všech možností .Řešení
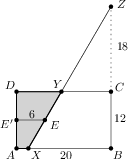
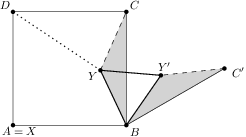
Mějme obdélník se stranami a . Na polopřímce leží bod takový, že . Bod leží uvnitř , přičemž platí, že vzdálenost od i je . Přímka protíná strany a postupně v bodech a . Zjistěte obsah čtyřúhelníku . Výsledek: 72 Uvědomíme si, že je lichoběžník s výškou . Jelikož je v půlce výšky obdélníka, je také středem . Pak označíme patu kolmice z na jako a spočítáme hledaný obsahŘešení
Pro kolik přirozených čísel je číslo druhou mocninou přirozeného čísla? Výsledek: 1028 Pro všechna sudá čísla je číslo určitě druhou mocninou. Pro lichá čísla je druhou mocninou práve tehdy, když je druhou mocninou lichého čísla. Sudých čísel do 2012 je 1006. Největší druhá mocnina, která je maximálně 2012, je 44. Vyhovují tedy i druhé mocniny lichých čísel do 44, těch je 22. Celkem máme .Řešení
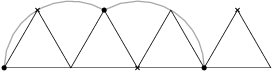
Mějme rovnostranný trojúhelník se stranou položený na podlaze. Jeden z jeho bodů obarvíme na červeno. Trojúhelník kutálíme po podlaze a třikrát ho překlopíme. Jak dlouhou dráhu projde červený bod? Výsledek: Uvědomíme si, že červený bod se pohybuje po obloucích kružnice (jeden bod vždy zůstává na místě a vzdálenost červeného bodu je od něho konstantní). Dvakrát projde z obvodu kružnice a jednou zůstane na místě. Dohromady projde dráhu délky .Řešení
Najděte nejmenší kladné číslo složené pouze z nul a jedniček, které je dělitelné . Výsledek: Číslo musí být dělitelné a (). Pokud je kladné, není složené jen ze samých nul, a tedy obsahuje alespoň jednu jedničku. Z dělitelnosti 9 máme, že počet jedniček je dělitelný 9, takže jich je alespoň 9. Z dělitelnosti 25 víme, že číslo končí jedním z dvojčíslí . Vyhovuje pouze . Takže číslo je alespoň .Řešení
Bill je dost starý na to, aby volil, ale ne na to, aby mohl využívat důchodcovskou slevu (tj. jeho věk je mezi 18 a 70 lety). Je o něm známo, že před lety ( je přirozené číslo) byl jeho věk odmocninou ze součtu jeho současného věku a . Billův věk je druhou mocninou přirozeného čísla. Najděte . Výsledek: 28 Označme Billův věk . Ze zadání víme, že je aritmetickým průměrem přirozeného čísla a jeho druhé mocniny . Nabývá tedy některé z hodnot , , , , nebo . Z této nabídky je druhou mocninou jedině , takže .Řešení
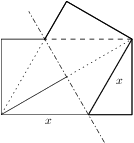
Přeložíme levý dolní roh obdélníkového papíru k pravému hornímu. Vznikne tak útvar rozdělený na tři trojúhelníky, jejichž strany tvoří okraje papíru a čára přehybu. Pro jaký poměr délek stran papíru je poměr obsahů těchto tří trojúhelníků ? Výsledek: Cokoliv z a Překládáme podle přímky procházející středem obdélníka, která je kolmá na úhlopříčku. Příčky obdélníka, které po přehnutí splynou s okrajem papíru, tak odseknou dva shodné trojúhelníky, přičemž zbylý útvar je kosočtverec o straně . Máme-li respektovat poměr obsahů ze zadání, zabere tento kosočtverec obsahu obdélníka. Jeho strana tak tvoří delší strany obdélníka a posléze vidíme, že je složen ze dvou rovnostranných trojúhelníků. Kratší strana obdélníka má pak délku . Odtud nalezneme hledaný poměr.Řešení
Kolik je trojciferných čísel dělitelných šesti takových, že v nich je každá cifra větší než ? Výsledek: 16 Číslo má být dělitelné , a proto musí končit cifrou nebo . Stejně tak je číslo dělitelné i třemi, a proto je jeho ciferný součet dělitelný třemi, tedy součet prvních dvou cifer musí dávat po dělení 3 zbytek 1 (je-li poslední cifra ) nebo (je-li poslední ). Zbytek umíme dostat jako součet čísel se zbytky , (záleží i na pořadí cifer, takže máme možností). Podobně zbytek umíme dostat jen jako , (znovu máme možností).Řešení
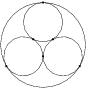
Jsou dány tři kružnice s poloměrem takové, že každé dvě z nich mají vzájemný vnější dotyk. Těmto kružnicím opíšeme kružnici tak, aby se jí zevnitř dotýkaly všechny tři kružnice. Vypočítejte poloměr kružnice .
Výsledek:
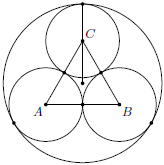
Označme , , středy třech menších kružnic. Trojúhelník tvořený těmito body je rovnostranný se stranou délky . Jeho výška má délku . Výšky trojúhelníku se protínají ve středu kružnice , označme ho , dokonce jsou zároveň také těžnicemi, a proto . Poloměr je potom jenom o poloměr menší kružnice větší než .
Nechť je přirozené číslo. Jaké cifry může mít číslo na místě jednotek, pokud má na místě desítek cifru ? Výsledek: Nechť pro nějaké celé číslo a cifru . Potom . Cifra na místě desítek bude lichá tehdy, pokud desítková cifra bude lichá. Proto je nebo . Poslední cifra je v obou případech .Řešení
Napíšeme-li čísla v nějakém pořadí za sebe, získáme něco, čemu budeme říkat -řetězec. Jeden z možných -řetězců délky 11 je tak například:
Pro jaké nejmenší existuje -řetězec, který je palindromem (tj. čte se stejně odpředu jako odzadu)? Výsledek: 19 Následující -řetězec je palindromem: Ukážeme, že je nejmenším takovým číslem. Uvědomíme si, že jen jedna cifra se může v palindromickém -řetězci vyskytnout licho-krát (konkrétně ta prostřední). Pro zřejmě tato podmínka není splněná. Podobně, pro se obě cifry a vyskytují právě jednou, takže zase nemůže být -řetězec palindromem.Řešení
Najděte všechny trojice kladných reálných čísel , a , pro které platí , a . Výsledek: Sčítáním rovnic dostaneme . Protože hledáme , , kladná, tak po vydělení dvěma a odmocnění máme . Zpětným dosazením do původních rovnic dostáváme , , , odkud snadno získáme řešení .Řešení
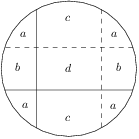
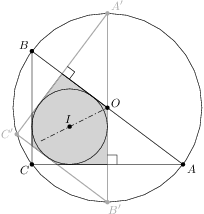
Mějme kruh s poloměrem a v něm dvě kolmé tětivy, které dělí kruh na části. Součet obsahů části s nejmenším obsahem a části s největším obsahem je roven součtu obsahů zbylých dvou částí. Jaká je maximální možná vzdálenost delší tětivy od středu kružnice? Výsledek: 0 Vezměme nějaké dvě tětivy s vlastností ze zadání. Nakreslíme dvě další tětivy, které s nimi budou středově souměrné podle středu kružnice. Rozdělili jsme tak kruh na částí, přičemž některé z nich mají díky souměrnosti stejné obsahy. Označme obsahy jednotlivých částí , , , jako na obrázku. Užijeme-li nyní podmínku ze zadání na původní dvě tětivy, obdržíme odkud plyne . Proto musí alespoň jedna tětiva procházet středem kruhu.Řešení
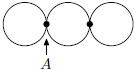
Strážník má za úkol hlídat tři objekty. Jeho obchůzkové trasy jsou na obrázku. Jedna obchůzka začíná v bodě , projde přes každý úsek právě jednou a vrátí se na začátek. Kolik různých obchůzek existuje, pokud záleží na směru obcházení budovy?
Výsledek:
Bod dotyku druhé a třetí kružnice označme . Během obchůzky šel někdy strážník z bodu do bodu a někdy potom po druhé cestě z bodu do bodu . Máme dvě možnosti, jak tuto dvojici cest uskutečnit (první horem nebo první spodem). Když strážník přijde do bodu , musí obejít pravé kolečko, jsou opět dvě možnosti, jak. Také jsou dvě možnosti, jak obejít levé kolečko, ale u něj máme dokonce dvě možnosti, kdy ho strážník obejde. Může tak učinit buď na začátku nebo na konci. Celkový počet možností tedy je 2 (možnosti chození mezi a ) krát 2 (možnosti, jak obejít pravé kolečko) krát 2 (možnosti, jak obejít levé kolečko) krát 2 (možnosti, kdy obejde levé kolečko).
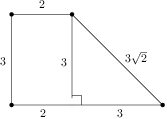
Lichoběžník má základny délek a a ramena délek a . Jaký má obsah? Výsledek: Rovnoběžka s kratším ramenem rozdělí lichoběžník na rovnoběžník a trojúhelník se stranami , , , který je tedy rovnoramenný pravoúhlý. Rovnoběžník je proto obdélník. Obsah teď snadno spočteme jako .Řešení
V řadě za sebou stojí lidí, kteří se chtějí seřadit podle výšky tak, aby vepředu stál ten nejvyšší. V jednom tahu si mohou vyměnit místo dva lidé stojící těsně za sebou. Kolik nejméně tahů je potřeba na to, aby se tímto způsobem všichni seřadili, ať už stojí na začátku libovolně? Výsledek: Každému pořadí lidí přiřadíme hodnotu , což bude počet dvojic (nejen sousedních) lidí takových, že menší z nich stojí před větším. V jednom tahu lze snížit nebo zvýšit o 1, přičemž pokud je , lze ho vhodným tahem snížit. Na začátku je nejvýše , a to když jsou všichni lidé v opačném pořadí. Na seřazení je tedy potřeba (a naopak vždy stačí) tahů.Řešení
Monča žije v ovocném státě, kde se platí pouze mincemi v hodnotách a . Kdyby měla Monča neomezenou zásobu obou druhů mincí, jaká je nejvyšší celočíselná hodnota, kterou by jimi neuměla zaplatit? Výsledek: 59 Pokud umíme zaplatit hodnotu s nějakým zbytkem po dělení , umíme už zaplatit libovolnou vyšší hodnotu se stejným zbytkem. Pro každý zbytek postupně zjistíme, kdy ho poprvé dosáhneme. Zbytek po dělení změníme jen použitím čísla . Takže dává , dává , dává , dává , dává , dává a dává . Máme všechny zbytky a od jsou už všechny hodnoty určitě dosažitelné. Poslední nedosažitelná hodnota má zbytek 3 a nejvyšší takovou je .Řešení
Rozdělíme kruh s poloměrem libovolným způsobem na čtyři souvislé části. Jaký nejmenší obvod může mít část s největším obsahem? Pokud je částí s největším obsahem víc, vybereme tu s nejmenším obvodem. Výsledek: Nejmenší možný obsah největší části je čtvrtina obsahu kruhu. Souvislá část s daným obsahem má nejmenší obvod, pokud má tvar kruhu. Takže rozsekneme-li původní kruh tak, že všechny části budou mít obsah právě čtvrtinu obsahu původního kruhu a jedna z těch částí bude mít kruhový tvar, tak jsme hotovi. To se dá udělat například vyseknutím kružnice soustředné s původním kruhem a polovičním poloměrem, přičemž zbytek rozřežeme na tři stejné části. Malá kružnice má obvod .Řešení
Najděte součet všech reálných čísel , pro která mají rovnice a alespoň jeden společný reálný kořen. Výsledek: Nechť je společným řešením obou rovnic. Odečtením rovnic dostaneme , takže buď nebo . V prvním případě je jejich společný kořen a dosazením do jedné z rovnic vypočítáme . V případě, že , jsou rovnice identické, ale jejich kořeny nejsou reálné.Řešení
Kolik je takových osmiciferných přirozených čísel, že po škrtnutí jejich první cifry zůstane číslo -krát menší než původní? Výsledek: Nechť je číslo, které nám zůstane po škrtnutí první cifry. Původní číslo potom musí být , kde je škrtnutá cifra. Má platit , což se dá upravit na . Levá strana je nenulová a dělitelná 17, proto musí být také pravá, což však není možné.Řešení
Mějme pravoúhlý trojúhelník, jehož všechny strany mají celočíselnou délku. Jaký největší obsah může mít, pokud má jedna z jeho stran délku ? Výsledek: Délku 2012 bude mít jistě kratší odvěsna. Musí platit Pythagorova věta . Protože obsah pravoúhlého trojúhelníka je , tak chceme maximalizovat délku druhé odvěsny . A to je stejná úloha jako minimalizovat rozdíl délek přepony a této odvěsny. Je-li , tak nesedí parita v Pythagorově větě. Dosazením do Pythagorovy věty dostaneme jednoduchou rovnici pro .Řešení
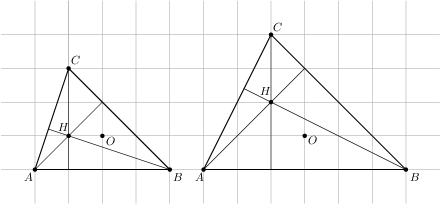
Nechť je trojúhelník se středem kružnice opsané a průsečíkem výšek , přičemž všechny body , , , a mají celočíselné souřadnice a žádné dva z nich nesplývají. Jaký je druhý nejmenší možný poloměr kružnice opsané trojúhelníku ? Výsledek: Najdeme si čtverečkovaný papír nebo si nakreslíme čtverečkovanou plochu. Ještě jednou si přečteme zadání, že všechny body mají být navzájem různé. Do počátku vyznačíme střed kružnice opsané a postupně zkoušíme poloměry: . Pro poloměry , , a vidíme, že je vždy jeden z vrcholů trojúhelníka zároveň průsečíkem výšek. Pro a jsme schopni zkonstruovat trojúhelníky, pro které jsou splněny podmínky zadání.Řešení
Najděte největší přirozené číslo takové, že číslo je dělitelné . Výsledek: 14 Vícenásobným použitím vzorce dostáváme V rozvoji je každý člen kromě dělitelný dvěma právě jednou, neboť pro dává zbytek po dělení čtyřmi.Řešení
Když počítáme součin cifer daného čísla, potom součin cifer tohoto součinu, potom znova součin cifer nového součinu atd., nutně po jistém počtu kroků dospějeme k jednocifernému číslu. Tento počet kroků nazýváme vytrvalostí čísla. Např. číslo má vytrvalost , protože (1. krok) a (2. krok). Najděte největší sudé číslo s navzájem různými nenulovými ciframi a vytrvalostí . Výsledek: Vyzkoušejme nejdříve největší číslo, které splňuje podmínku různých nenulových cifer. Tím je , ale má jen vytrvalost 2, protože a potom kvůli nule na konci získáme v druhém kroku 0. Uvědomíme si, že 0 na konci dostaneme vždy, když mezi ciframi čísla bude nějaké sudé číslo a 5 zároveň. Proto zkusíme nejdřív vyhodit pětku. Vytrvalost čísla je 3, neboť . Poslední podmínku splníme přehozením posledních dvou cifer na a máme výsledek.Řešení
Když prodloužíme strany a konvexního čtyřúhelníku , protnou se v bodě . Označme a postupně středy úhlopříček a . Najděte poměr obsahů trojúhelníku a čtyřúhelníku . Prozradíme vám, že tento poměr je stejný pro každý konvexní čtyřúhelník , jehož strany a nejsou rovnoběžné. Výsledek: Uvažme čtyřúhelník, v němž body a splynou. Pak je střední příčka v a hledaný poměr obsahů je pak zřejmě .Řešení
Krychloví termiti vyhloubili skrz krychli o straně cm v každém směru 4 rovné chodbičky jako na obrázku a opustili ji. To, co z krychle zbylo, chceme obarvit barvou proti termitům. Kolik centimetrů čtverečních musíme obarvit?
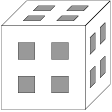
Výsledek:
270
Podíváme se na děravou kostku shora a spočítáme obsah všech plošek, které se na nás „dívají“ – jsou orientované směrem nahoru. V hloubce 0 (ve stěně kostky) je jich . V hloubce 2 je jich tolik, kolik je vyvrtaných chodeb z boku mínus počet vyvrtaných chodeb shora: . Hloubka 4 je stejný případ jako hloubka 2. Z každé strany kostky je situace stejná, takže máme celkem plošek.
Máme kruh o poloměru a stojíme v bodě, který leží na jeho obvodu nejvíce vlevo. Můžeme se hýbat jen doprava a nahoru. Jak je dlouhá nejdelší trasa, kterou můžeme ujít, když nechceme opustit kruh? Výsledek: Nejprve si uvědomíme, že pro libovolnou cestu existuje cesta stejné délky, která jde nejdřív jen doprava a potom už jen nahoru. Nyní proto uvažujme už jen takovéto cesty. Nejdelší cesta musí procházet středem kruhu. Označme vzdálenost, kterou urazíme doprava od středu kruhu, a vzdálenost, kterou urazíme od středu nahoru. Protože nejdelší cesta skončí na obvodu kružnice, platí a chceme maximalizovat . To je stejná úloha jako maximalizovat . Z triviální nerovnosti máme . Rovnost nastává právě tehdy, když máme rovnost pro , takže . Spolu s cestou do středu kruhu je výsledek .Řešení
Jaký je největší dělitel čísla takový, že po vydělení dává zbytek ? Výsledek: Zbytek součinu je stejný jako součin zbytků jednotlivých činitelů, např. zbytek . Aby byl konečný zbytek 5, číslo nesmí být dělitelné ani , takže z musíme vyhodit všechny dvojky a trojky. Zůstane nám číslo a to dává zbytek 1. Všechny činitele dávají zbytek 1 nebo 5, takže nám stačí vyhodit jedno číslo se zbytkem 5. Nejmenším takovým je samozřejmě 5.Řešení
Mějme krychli a v ní následujících bodů: vrcholy krychle, středy hran, středy stěn a střed krychle. Kolik je přímek, které procházejí právě třemi z těchto bodů? Výsledek: 49 Rozdělíme si všechny přímky do třech nezávislých kategorií. Přímek, které procházejí středem krychle, je . Přímky, které procházejí středem stěny a neprocházejí středem krychle, jsou pro každou stěnu 4 a celkem je jich tedy 24. Zbyly nám už jen přímky totožné s hranami krychle, kterých je 12. Dohromady máme přímek.Řešení
Soutěže trvající několik dní (alespoň jeden) se zúčastnilo účastníků. Každý den všichni účastníci získali skóre bodů, přičemž žádní dva neměli v daném dni stejný počet bodů. Po konci soutěže měl každý účastník celkem za všechny dny skóre bodů. Najděte součet všech takových , pro které je to možné. Výsledek: Je zřejmé, že . Označme dále počet dnů, po něž soutěž probíhala. Dohromady se každý den rozdalo bodů, což dává celkový součet bodů. To je ale zároveň rovno . Porovnáním dostáváme . Po chvilce zkoušení zjistíme, že pro umíme najít způsob, jakým účastníci mohli dostávat body během soutěže, a naopak pro taková soutěž neexistuje. Součet všech je proto .Řešení
Šavlík dostal k narozeninám dort a teď ho nožem rozřezává. Každý řez má tvar roviny. Například dvěma řezy lze dort rozřezat na čtyři části a třemi řezy na osm částí. Kolik nejvíc částí může Šavlík získat pěti řezy? Výsledek: Pro jednoduchost uvažujme nekonečný trojrozměrný prostor, který rozřezáváme nekonečnými rovinami. Ve chvíli, kdy už je prostor nějak rozřezaný, nám další rovina přidá tolik nových částí, kolik existujících částí rozřeže. Vezměme si přímky, které jsou průsečnicemi nové roviny se starými rovinami. Počet nových částí je stejný jako počet oblastí, na které tyto přímky rozdělí novou rovinu. Tedy , kde je výsledek pro řezů a je počet nových částí = počet oblastí, na které umíme rozdělit rovinu přímkovými řezy. Kreslením na papír získáme maximální hodnoty pro a jako , , a . Pro tak dostávame výsledek .Řešení
Osmiramenná hvězda je těleso, které vznikne přilepením pravidelných čtyřstěnů na všechny stěny pravidelného osmistěnu. Hrany osmistěnu i všech čtyřstěnů mají délku . Jaký má osmiramenná hvězda objem? Výsledek: Máme dva typy těles. Pravidelný čtyřstěn se stranou 1 a čtyřboký jehlan se všemi stranami délky 1. Čtyřboký jehlan má obsah podstavy 1 a výšku vypočteme z Pythagorovy věty (hrana, úsečka z vrcholu do středu podstavy a výška tvoří pravoúhlý trojúhelník) jako , takže má objem . Podobně čtyřstěn má obsah podstavy (rovnostranný trojúhelník) a výšku , takže má objem . Když to celé sečteme, dostáváme .Řešení
Po cestě jde stopař. Šance, že v nejbližších minutách stopne auto, je . Pokud je pravděpodobnost stopnutí auta v každém okamžiku stejná, jaká je pravděpodobnost, že stopař stopne auto v nejbližších pěti minutách? Výsledek: Zkusme raději počítat pravděpodobnost, že stopař auto nestopne. Pro 20 minut to je . Když pravděpodobnost nestopnutí auta stopařem během 5 minut je , pak pro 20 minut to je . Tedy . Potom pravděpodobnost stopnutí auta během 5 minut je .Řešení
Vandal a moderátor upravují článek na wikipedii. Na začátku byl článek bez chyby. Každý den přidá vandal jeden chybný údaj. Na konci každého dne má moderátor šanci na nalezení každé jednotlivé chyby, která ještě v článku je. Jaká je pravděpodobnost, že po třech dnech bude článek bezchybný? Výsledek: Pro každou chybu spočítáme pravděpodobnost, že v článku nevydrží do konce. Pravděpodobnost, že nějaká chyba vydrží dní, je a pravděpodobnost, že nějaká chyba nevydrží dní, je . Protože nevýdrž jednotlivých chyb je nezávislá, tyto pravděpodobnosti jednoduše vynásobíme: .Řešení
Z neomezené zásoby červených, modrých a žlutých karet si jich vybereme patnáct. Za každou kartu se dostávají body podle následujících pravidel:
Kolik nejvíc bodů můžeme získat? Výsledek: Nechť je počet červených karet, je počet modrých karet a je počet žlutých karet. Obraťme vztah červených a modrých karet. Potom každá červená karta přispívá k celkovému skóre body (jeden bod za sebe a dva za každou modrou kartu) a každá žlutá karta přispívá body. Pro se nám vyplatí změnit všechny červené karty za žluté. Pro je maximální skóre 15. Pro je skóre vždy 42. Pro je skóre a dále víme, že . Maximum nastává při a , což dává skóre .Řešení
Olin má jednu -stěnnou hrací kostku a Vejtek má tři -stěnné hrací kostky. Jaká je pravděpodobnost, že po hození kostkami bude hodnota na Olinově kostce větší než součet hodnot na Vejtkových kostkách? Výsledek: Uvědomíme si, že oba hody mají symetrické rozdělení. Tj. pravděpodobnost, že padne na dvacetistěnné kostce, je stejná jako pravděpodobnost, že padne (od 1 do 20). A podobně pravděpodobnost, že padne na třech šestistěnných kostkách, je stejná, jako že padne (od 3 po 18). Podobnou úvahou zjistíme, že pravděpodobnost výhry Olina je stejná jako pravděpodobnost výhry Vejtka. Proto je výsledek , kde je pravděpodobnost remízy. A ta je , protože ať hodí Vejtek třemi kostkami libovolnou hodnotu, má vždy Olin šanci , že se do ní trefí.Řešení
Mějme tabulku . Řádky, resp. sloupce očíslujeme postupně zleva doprava, resp. shora dolů čísly od do . Do každého políčka vepíšeme součin čísla řádku a čísla sloupce, ve kterých se políčko nachází. Voják stojí na políčku v levém horním rohu a chce se dostat na políčko v pravém dolním rohu. Může chodit jen doprava a dolů (ne šikmo). Nábojovým číslem nazveme součin čísel na políčkách, po kterých voják cestou přešel (včetně prvního a posledního). Jaký je největší společný dělitel všech nábojových čísel, která můžeme uvažovat? Výsledek: Je třeba si uvědomit, jaká čísla musí voják posbírat a jakým se naopak může vyhnout. Každá cesta nasbírá každé číslo alespoň dvakrát (jednou za sloupec a jednou za řádek). Pro každé číslo kromě a existuje cesta, která prochází -tým řádkem a -tým sloupcem právě jednou (takové velké „L-ko“). Proto budou ve výsledném součinu právě dvakrát. Jelikož v pravém dolním rohu () nasbíráme hned dvě desítky a tah předtím jsme museli taktéž sebrat jednu desítku, tak 1000 dělí výsledek. Je jednoduché se přesvědčit, že víc než tři desítky nemusíme posbírat.Řešení
Mějme trojúhelník s výškami o délkách , a . Jaký je jeho obvod? Výsledek: Z faktu, že obsah trojúhelníku je polovina součinu jeho výšky a strany, dostáváme, že trojúhelník bude podobný s trojúhelníkem o stranách délek 2, 3, 4. Vyjádříme jednu z výšek trojúhelníku pomocí jeho stran. Můžeme například použít Heronův vzorec pro strany , a a potom dát do rovnosti s obsahem . Takže , z čehož dostaneme a obvod je tedy .Řešení
Najděte největší přirozené číslo , pro které je výraz racionální. Výsledek: Označme . Potom platí . Řešením kvadratické rovnice pro je , a protože má být racionální, tak musí platit , kde je racionální číslo. Úpravou výrazu dostaneme . Aby bylo celé, musí být i celé, protože když je zlomek v základním tvaru, tak má být celé číslo, a tedy by muselo dělit , což je spor s tím, že je v základním tvaru. Další úpravou , tedy musí být liché, a aby , tak , odkud .Řešení
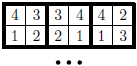
Mějme Maxičtverec tvořený devíti čtvercovými kachličkami. Každá kachlička je rozdělená na čtyři stejné čtverečky, do kterých jsou vepsána čísla , , a (každé právě jednou). Dvě kachličky se můžou dotýkat jen čtverečky se stejnými čísly (jako kostky domina). Kolik různých Maxičtverců existuje?
Výsledek:
Prostřední kachličku si zvolíme pevně. Nyní si všimneme, že čísla na pozicích a (kde značí levý horní čtvereček) mohou nabývat pouze dvou různých hodnot, což nám dohromady dává čtyři možnosti. U tří z nich je doplnění zbytku tabulky jednoznačné, u čtvrté mohou nastat čtyři případy. Vzhledem k tomu, že máme možností, jak zvolit prostřední kachličku, výsledek bude .
Vejtek svoje oblíbené číslo (zapsané v desítkové soustavě a bez nuly na začátku) nazývá langoš. Pro langoš platí:
Určete hodnotu langoše. Výsledek: 1010309 Zaměříme se na podmínku, že číslo o 1 větší je dělitelné . Z toho je hned zřejmé, že poslední cifra musí být 9. Kvůli dělitelnosti třemi je ciferný součet tvaru . Ze zadání je ciferný součet langoše dvojnásobek počtu jeho cifer. Protože jsou ciferné součty sudé, tvaru a větší než 9, přicházejí v úvahu 14 a 20. Jim odpovídají počty cifer , resp. . Protože se střídají sudé a liché cifry, tak nejmenší čísla splňující všechno kromě dělitelnosti 7 jsou 1010109 a 2101010109, které mají ciferné součty 12 a 15. Druhé číslo má lichý ciferný součet, a tedy neumíme dosáhnout součtu 20. V první případě nám stačí zvětšit ciferný součet o 2, tedy zvětšit jednu z cifer o 2. Snadno se přesvěčíme, že jediná možnost (kvůli dělitelnosti 7) je číslo 1010309.Řešení
Pepa si vymyslel takové čtyřciferné číslo , že poslední čtyři cifry čísla tvoří opět číslo . Najděte všechna možná Pepova čísla. Výsledek: 9376 Přeformulováním zadání dostaneme pro nějaké přirozené . Číslo dělí pravou stranu, a proto dělí buď nebo . Podobně dělí buď nebo . Z první dělitelnosti plyne, že je tvaru , kde a . Protože dává zbytek 1 po dělení 16, tak dává zbytek po dělení 16. Z druhé dělitelnosti proto plyne . Čtyřciferný výsledek dostaneme jedině pro , čemuž odpovídá . Platí , a proto 9376 je jediným možným a také vyhovujícím výsledkem.Řešení
Palindrom je číslo, které se čte odpředu stejně jako odzadu jako třeba 121. Zjistěte součet všech pěticiferných palindromů. Výsledek: Všech pěticiferných palindromů je stejně jako všech trojciferných čísel, a dokonce existuje jednoduché přiřazení mezi nimi. Číslu umíme přiřadit palindrom pro a . Celkový součet si rozložíme na součty po cifrách. Každé přispěje , každé přispěje a každé přispěje k celkovému součtu. Každá z možností pro se objeví v součtu 100krát a každá z možností pro a se objeví v součtu 90krát. Proto je celkový výsledekŘešení
Mějme čtyři lichá přirozená čísla , , a , pro která platí . Kolika různými způsoby můžeme tato čísla vybrat? Výsledek: Nejprve si úlohu převedeme na jednodušší tak, aby se výsledek nezměnil. Označíme si a stejným způsobem označíme i , a pro , a . Potom platí pro kladná celá , , a . Pro každou čtveřici , , a ze zadání existuje vyhovující čveřice , , a a naopak. Toto už je standardní úloha. Řešíme ji tak, že si vezmeme 47 bílých a 3 černé kuličky. Postavíme je do řady tak, že černé kuličky rozdělí bílé kuličky na čtyři (potenciálně prázdné) úseky, které označují ,, a . Například pokud jsou černé kuličky na pozicích 5, 6 a 25, tak úseky bílých jsou 1-4, prázdný, 7-24 a 26-50 a , , a . Zase je vidět, že pro každé , , a existuje právě jedno odpovídající rozestavení kuliček a naopak. Takže řešením je počet rozestavení 3 černých kuliček na 50 pozicích, kterých je .Řešení
Najděte jediné jedenácticiferné přirozené číslo začínající jedničkou takové, že když ho zapíšeme dvakrát za sebou, vyjde druhá mocnina přirozeného čísla. Výsledek: Číslo vzniklé zapsáním původního čísla dvakrát za sebou je -násobkem čísla . Proto když zvolíme , tak . Musíme ješte zvolit tak, aby bylo jedenácticiferné a začínalo jedničkou. Poslouží nám a ze zadání víme, že je jediné takové.Řešení
V rovině jsou dány dva různé trojúhelníky se stranami 18, 24, 30, které sdílí jak kružnici vepsanou, tak kružnici opsanou. Určete obsah mnohoúhelníku určeného jejich průnikem. Výsledek: 132 Označme jeden trojúhelník (, ). Jelikož , je pravoúhlý a pro poloměry kružnice opsané a vepsané platí a . Existuje jediný průměr kružnice opsané různý od , který se dotýká kružnice vepsané – ten symetrický s podle přímky . Shodou okolností leží na ose strany . Ta totiž prochází bodem , a jelikož má od vzdálenost 12, má od vzdálenost 6. Druhý trojúhelník tak bude symetrický s podle a zároveň bude a . Zbývá si rozmyslet, že průnik dvou trojúhelníků získáme z trojúhelníku odečtením tři malých trojúhelníčků, jejichž rozměry postupně určíme jako (u ), (u ) a (u ). Konečně obsah průniku je rovenŘešení
Mějme mřížku . Každý čtvereček mřížky chceme vybarvit bílou nebo černou barvou tak, aby platilo, že v každém řádku i sloupci jsou právě dva černé čtverečky. Kolika různými způsoby to můžeme udělat? Výsledek: 2040 Postupně obarvíme deset políček černě. Označme políčka až . Búno jsou obarvena políčka , (výsledek pak ze symetrie stačí vynásobit ) a (a čtyřmi). Pokud je ve druhém řádku obarveno políčko , stačí určit počet vyhovujících obarvení tabulky , což je 6. Pokud je v něm obarveno jiné políčko, ať je to búno (násobíme třemi), a ve třetím sloupci ještě (opět třemi). Pokud je teď obarveno , je jediná možnost, jak obarvení dokončit (, , , ). V opačném případě jsou možnosti čtyři (búno je ve třetím řádku obarveno a ve čtvrtém sloupci ). Celkový počet obarvení je protoŘešení
Mějme body a uvnitř čtverce se stranou o délce 1. Dálkou vrcholu čtverce označme jeho vzdálenost k bližšímu z bodů a . Jaký je nejmenší možný součet dálek vrcholů čtverce? Výsledek: První odhad získáme, pokud a zvolíme jako vrcholy čtverce. Potom je součet dálek 2. Pomocí trojúhelníkových nerovností zjistíme, že pokud je nebo nejblíž k právě 0, 2 nebo 4 vrcholům, tak součtu menšího než 2 nedosáhneme. Proto nechť je právě ke třem vrcholům (, a ) blíž než . Chceme minimalizovat , ale může být nula pro . Je známo, že součet tří vzdáleností v trojúhelníku je nejmenší, pokud úsečky , a svírají úhly 120 stupňů. (To lze ověřit otočením trojúhelníka podle bodu o stupňů na , a minimalizací délky lomené čáry . Optimální bude úsečka , jejíž délku snadno vyjádříme pomocí Pythagorovy věty.)Řešení
Parkoviště sestává z parkovacích míst pravidelně rozložených v jedné řadě a označených čísly až . Postupně tam po jednom zaparkuje aut, přičemž postupují následovně:
Jaká je pravděpodobnost, že poslední auto zaparkuje na místě s číslem ? Výsledek: Aby mohlo být místo s číslem 1 obsazené jako poslední, musí být místo s číslem 2 obsazené jako první (s pravděpodobností ) a hned po něm se obsadí pozice . Potom se zaplní některá místa od do , dokud nezůstanou pouze mezery velikosti 1 a 2. V takovém případě je pravděpodobnost, že 1. místo bude obsazené jako poslední, rovna převrácené hodnotě počtu míst, neboť každé místo má stejnou šanci, že bude obsazeno jako poslední. Uvědomíme si, že budeme-li se dívat pouze na velikosti mezer a postupně obsazovat největší, zbyde nám vždy stejný počet mezer velikosti 1 a 2, a proto je umíme jednoznačně spočítat. Nechť je počet míst, která zůstanou volná, mohou-li auta parkovat na místech za sebou, přičemž první a poslední je obsazené. První auto se postaví do středu a zbydou případy a . Máme tedy rekurentní vyjádření a s počáteční podmínkou a . Když si s tím trochu pohrajeme a spočítáme pro malé hodnoty, dobereme se k explicitnímu vyjádření: Proto a celková pravděpodobnost je .Řešení
Najděte všechna reálná splňující
Výsledek: Jelikož řešíme po substituci rovnici Pro každé pak snadno zjistíme odpovídající .Řešení