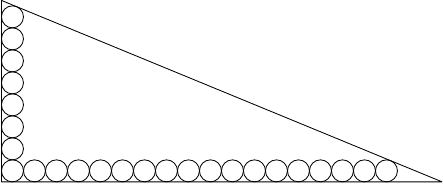
Rovnostranný trojúhelník se stranou délky je rozdělený na rovnostranných trojúhelníčků se stranou délky . Množinu vrcholů těchto trojúhelníčků nazveme nezávislou, pokud pro každé dva různé body platí, že úsečka není rovnoběžná s žádnou stranou trojúhelníku . Kolik nejvíce vrcholů může nezávislá množina obsahovat?Řešení
Výsledek:
1346
Každému vrcholu v mřížce můžeme přiřadit trojici jeho vzdáleností od tří stran trojúhelníku (jako jednotku této vzdálenosti budeme brát výšku trojúhelníčku). Součet těchto vzdáleností je vždy roven . Naopak, libovolná trojice nezáporných celých čísel se součtem udává právě jeden vrchol mřížky. Můžeme tedy namísto vrcholů pracovat ekvivalentně jen s těmito trojicemi, kterým budeme říkat souřadnice.
Podmínka nezávislosti v řeči souřadnic znamená, že žádné dvě trojice v množině nesmí mít stejnou první, druhou nebo třetí souřadnici. Nechť
|
je nezávislá množina. Protože jsou navzájem různá nezáporná celá čísla, jejich součet je aspoň
|
Totéž platí pro součty a . Na druhé straně máme pro každé , tedy
|
Z toho plyne, že
neboli .
Následující dvě posloupnosti bodů tvoří dohromady nezávislou množinu o velikosti :
|
Hledaný maximální možný počet prvků nezávislé množiny je tedy
.
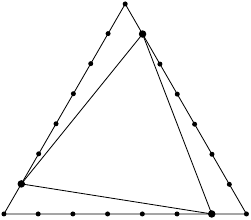
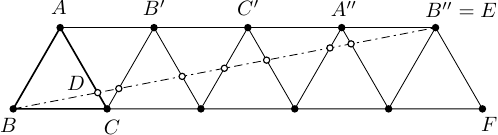
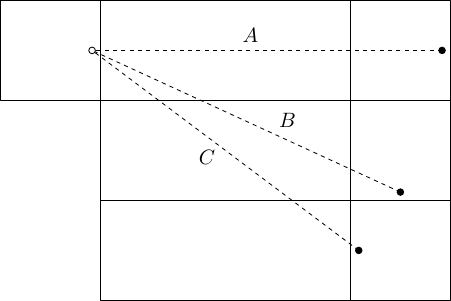
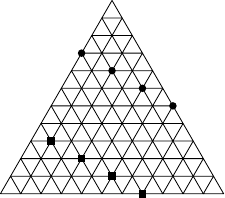
Na obrázku je konstrukce nezávislé množiny pro trojúhelník se stranou délky :