Zadání a řešení úloh

Výsledek:

$58$

Stáří Jarmiliných dětí jsou nutně $21$, $21+4$, $\text{…}$, $21+4\cdot 4$ roků. Ona sama je o $21$ let starší než její nejstarší potomek, takže jí je $21+4\cdot 4+21=58$ let.

Výsledek:

$56$

U vrcholu $S$ je pět párů vrcholových úhlů a právě jeden úhel z každé dvojice je vnitřní úhel některé lopatky, tedy součet vnitřních úhlů lopatek při vrcholu $S$ je $\frac{360^{\circ }}{2}$. Protože jsou lopatky rovnoramenné trojúhelníky, musí být oba vnitřní úhly u krajních bodů každého z nich stejné. Když sečteme všechny vnitřní úhly v lopatkách, dostaneme $5\cdot 180^{\circ }$. Velikost úhlu označeného otazníkem je proto

Výsledek:

$32$

Pokud sečteme zadané počty studentů, kteří se zúčastnili (alespoň) jedné disciplíny, a od tohoto počtu odečteme zadané počty studentů, kteří se zúčastnili (alespoň) dvou disciplín, tak dostaneme všechny účastníky turnaje bez těch, kteří se zúčastnili všech tří disciplín. Výsledek je tedy $(22+13+15)-(8+7+6)+3=32$.

Výsledek:

$90$

Celkem máme pět sudých číslic. Abychom zaručili, že výsledek bude supersudé číslo, nesmí součet žádných dvou číslic při provádění tradičního sčítání „pod sebou“ přesáhnout desítku. Zároveň žádné číslo nezačíná nulou, proto máme právě tři možnosti na první dvě číslice hledaného čísla, dvě možnosti na třetí pozici, jednu možnost na čtvrtou a všech pět možností na poslední číslici. Celkově tedy existuje $3\cdot 3\cdot 2\cdot 1\cdot 5=90$ takových supersudých čísel.

Výsledek:

$\frac{25}{4}$

Víme, že součet obvodů původních hradeb musí dát obvod nové zdi. Označíme-li nový poloměr $r$, pak platí

Poloměr nové zdi je tedy součtem poloměrů původních zdí, $r=500$. Hledaný nárůst je tudíž dán poměrem $\frac{\pi \cdot 500^2}{\pi \cdot 200^2}=\frac{25}{4}$.

Výsledek:

$9316$

Protože Verčin PIN je dělitelný $137$ a $17$, musí být násobkem $137\cdot 17=2329$. Všimněme si, že toto číslo nesplňuje zadané podmínky a může být vynásobeno pouze $2$, $3$ nebo $4$, aby zůstalo čtyřciferné. Zbývají tedy následující možnosti: $2329\cdot 2=4658$, $2329\cdot 3=6987$ a $2329\cdot 4=9316$, jejichž ciferné součty jsou po řadě $23$, $30$ a $19$. Protože $19$ je z nich to nejmenší prvočíslo, hledaný PIN je $9316$ a Verča může s chutí vyrazit na zaslouženou cukrovou vatu.

Výsledek:

$27$

Předpokládejme, že každý ze shodných mnohoúhelníků má $n$ stran. Výsledný tvar musí mít $3(n-3)$ stran, protože tři strany každého mnohoúhelníku, včetně trojúhelníku, jsou sdílené. Nyní stačí pouze najít vhodné $n$. Z velikosti vnějšího úhlu rovnostranného trojúhelníku, který je $300^{\circ }$, a ze symetrie vyplývá, že vnitřní úhel shodných mnohoúhelníků je $150^{\circ }$. Protože součet úhlů v $n$-úhelníku je $(n-2)\cdot 180^{\circ }$, dostáváme rovnici $150n=180(n-2)$ s řešením $n=12$. Po dosazení do vzorce z prvního řádku dostáváme, že výsledný obrazec má $3\cdot 9=27$ stran, tudíž obvod $27$.

Výsledek:

$8081$

Pro úsporu časoprostoru říkejme rovnostranným trojúhelníkům jen trojúhelníky. Na obrázku je původní trojúhelník, dále $3\cdot 2020$ trojúhelníků sdílejících právě jeden vrchol s původním trojúhelníkem ($2020$ pro každý z vrcholů) a nakonec $2020$ otočených trojúhelníků, které s původním nesdílejí ani jeden vrchol. Je jednoduché nahlédnout, že všechny tyto trojúhelníky jsou navzájem různé a že žádné další existovat nemohou. Celkem tedy máme $1+3\cdot 2020+2020=8081$ hledaných trojúhelníků.

Výsledek:

$\sqrt{300}\doteq 17,32051$

Vnitřní úhly pravidelného osmiúhelníku mají velikost $135^{\circ }$. Verčou ustřižené rohy jsou rovnoramenné pravoúhlé trojúhelníky, které se navíc dají poskládat do čtverce, jehož strana je stejně dlouhá jako strana vystřiženého osmiúhelníku. Z toho vyplývá, že délka strany osmiúhelníku je rovna $\sqrt{300}$, neboť obsah poskládaného čtverce je $300$.

Výsledek:

$853$

Z druhé podmínky dostáváme, že alespoň jedna číslice čísla $n$ musí být $5$ a alespoň jedna musí být sudá, ale žádná není nula. Vezmeme-li toto v potaz, z první podmínky dostáváme následující možné trojice cifer obsažených v čísle $n$: $5,2,9$ nebo $5,4,7$ nebo $5,6,5$ nebo $5,8,3$. Z těchto možností pouze $5,8,3$ splňuje poslední zadanou podmínku a největší možné trojciferné číslo složené z těchto číslic je tedy $853$.

Výsledek:

$75928$

Největší číslice, které je možno dosáhnout odebráním nejvýše pěti číslic zleva, je $7$. Protože se toho dosáhne odebráním právě tří číslic zleva, je jasné, že zbývající číslice, které je nutné odebrat, jsou $0$ a $1$. Proto je číslo $75928$ hledaným číslem.

Výsledek:

$12$

Číslo $2021$ se vyskytne jako člen v $S_n$ právě tehdy, pokud pro nějaké kladné celé číslo $a$ platí $2021=1+\mathit{an}$. Jinými slovy $2020=\mathit{an}$, a tudíž $n$ musí být dělitelem $2020$. Rozklad na prvočísla nám dává $2020=2^2\cdot 5\cdot 101$, a tak víme, že každý dělitel je dán některou kombinací těchto čísel. Číslo dva můžeme vzít buď jednou, dvakrát nebo vůbec, to nám dává tři možnosti. Pět a sto jedna můžeme buď vzít, nebo ne, to dává dvě možnosti pro obě prvočísla. Celkem tedy máme $3\cdot 2\cdot 2=12$ možností, jak můžeme z těchto prvočísel poskládat dělitele $2020$. To znamená, že $2021$ je členem $12$ z Honzových posloupností.

Výsledek:

$510$

Pro každého robota $A$ můžeme určit okno a směr, kde by musel začínat jiný robot, aby trvalo co nejdéle, než se potkají. Je to to nejbližší okno v opačném směru, než kterým $A$ vychází, a směr pohybu druhého robota by musí být opačný než směr $A$. Vychází-li $A$ od jednoho z krajních oken, můžeme předpokládat, že začíná směrem pryč z chodby.

Ukáže se, že čas, který uplyne, než se tito dva roboti potkají, je pro každou výše popsanou dvojici robotů stejný: Oba dohromady totiž musejí ujít $80+90=170$ metrů, neboli každý z nich musí urazit $\frac{170}{2}$ metrů, což jim zabere $\frac{170}{2\cdot 10}\text{min}=8,5\text{min}=510\text{s}$.

Výsledek:

$42$

Nejprve zdůvodníme, že trojúhelníky $\mathit{APD}$ a $\mathit{BCP}$ pokrývají polovinu obsahu celého rovnoběžníku. Lépe je to vidět pro druhé dva trojúhelníky; jejich výšky vedené z bodu $P$ totiž dají v součtu výšku rovnoběžníku $h$ kolmou na $\mathit{AB}$, a součet jejich obsahů je proto $\frac{1}{2}h\cdot |\mathit{AB}|$.

Obsah trojúhelníku $\mathit{ABP}$ je tudíž roven $\left(\frac{1}{3}+3\right)\cdot 18-18=42$.

Výsledek:

$107$

Zadaná čísla jsou od sebe vzdálena $1486-1058=428$ a $2021-1486=535$. Abychom dostali stejný zbytek po dělení zadaných čísel číslem $d$, musí být jejich vzdálenosti násobky $d$. Největší společný dělitel čísel $428$ a $535$ je $107$, což je prvočíslo, a proto je to naše hledané číslo $d$.

Výsledek:

$3024$

Představme si, že deset náhradníků stojí v řadě vedle sebe. Je mezi nimi devět mezer, přičemž do každé z nich můžeme umístit nejvýše jednoho člena vedení. To lze provést $9\cdot 8\cdot 7\cdot 6=3024$ způsoby.

Výsledek:

$\frac{\sqrt{3}}{6}\doteq 0,288675$

Základna má obsah $1$, tudíž i stranu délky $1$. Protože je povrch celého jehlanu roven $3$, je povrch pláště roven $2$, tedy každá stěna má obsah $\frac{1}{2}$, což znamená, že výška každého stěnového trojúhelníku je rovna $1$. To také znamená, že rozpůlíme-li jehlan řezem skrze jeho vrchol a středy dvou protilehlých stran základny, dostaneme rovnostranný trojúhelník o straně délky $1$, jehož výška je též výškou Matějova jehlanu. Z toho spočítáme délku výšky jako $\frac{1}{2}\sqrt{3}$. Protože je objem jehlanu roven třetině součinu délky výšky a obsahu základny, je objem Matějova jehlanu roven $\frac{1}{3}\cdot \frac{1}{2}\sqrt{3}\cdot 1=\frac{1}{6}\sqrt{3}$.

Výsledek:

$2250$

Označme $x$ množství vína a $y$ množství vody v litrech, které Bára nalila do barelu. Víme, že $0,06y$ litrů vody se přeměnilo na víno a $0,1x$ litrů vína se přeměnilo na vodu. Množství vody (a vína) se nezmění právě tehdy, když

Vyjádřením $y$ a dosazením do rovnice pro celkový součet objemu vody a vína, $x+y=6000$, dostaneme, že

Bára tudíž do barelu nalila $2250$ litrů vína.

Výsledek:

$35$

Snadno nahlédneme, že poloměr vepsané kružnice rovnostranného trojúhelníku je poloviční oproti poloměru kružnice jemu opsané. Obsah kruhu ohraničeného vepsanou kružnicí je tedy $\frac{140}{4}=35$. Šedá oblast je přesně $\frac{1}{3}$ mezikruží mezi opsanou a vepsanou kružnicí. Její obsah je proto $\frac{140-35}{3}=35$.

Výsledek:

$4044$

Uspořádejme čísla sestupně podle velikosti a označme je postupně $c_1\ge c_2\ge \cdots \ge c_{2020}\ge c_{2021}\ge 1$. Chceme najít největší možnou hodnotu čísla $c_1$ takovou, že výše zmíněná čísla splňují rovnici

Rovnici vydělíme součinem na levé straně a za pomoci odhadů

a horního odhadu $c_1\cdot c_2$ pro všechny ostatní součiny dostaneme

Úpravou nerovnosti výše obdržíme

Pokud $c_2\ge 3$, pak platí $c_1\le 4044$. Volbou

získáme čísla, pro něž je splněna rovnice (1) a zároveň $c_1$ nabývá maximální možné hodnoty. Pokud $c_2\le 2$, pak víme, že mezi čísly

je $k\ge 0$ dvojek a $2020-k$ jedniček. Využitím těchto pozorování rovnice (1) přejde do tvaru

Všimněme si, že pro $k\le 1$ nemá rovnice řešení a pro $k\ge 2$ máme

Dokázali jsme tedy, že největší hodnota, které čísla mohou nabývat, je $4044$.

Výsledek:

$59$

Všimněme si nejdříve, že v trojúhelníku jsou právě tři políčka sousedící s jedním políčkem, právě tři sousedící se dvěma a právě tři sousedící se třemi políčky. To znamená, že pokud v jednom z políček bude prvočíslo, pak mezi zbylými osmi čísly bude ještě alespoň jeden jeho násobek. Dále platí, že jedničku není možné do trojúhelníku doplnit. Označme $S$ součet čísel vyplněných do trojúhelníku podle zadání.

Nechť je v trojúhelníku prvočíslo $p\ge 11$. Pak mezi zbylými osmi čísly musí být jeho násobek $k\cdot p$, kde $k\ge 2$. Vyplňme nyní všechna ostatní políčka tabulky nejmenšími možnými čísly nehledě na způsob, jak má být podle zadání trojúhelník vyplněn. To nás dovádí k odhadu

Dále nechť mezi čísly v trojúhelníku není prvočíslo $p\ge 11$. Rozebereme čtyři případy:

• V trojúhelníku jsou obě čísla $5$ a $7$:

  $$S\ge 5+k_5\cdot 5+7+k_7\cdot 7+2+3+4+6+8=(k_5+1)\cdot 5+(k_7+1)\cdot 7+23\ge 15+21+23=59.$$

• Do trojúhelníku jsme doplnili číslo $5$, ale ne číslo $7$:

  $$S\ge 5+k\cdot 5+2+3+4+6+8+9+\{\begin{array}{c}10\ge 20+32+10=62\text{pro}k\ge 3,\hfill \\ 12=15+32+12=59\text{pro}k=2.\hfill \end{array}$$

• V trojúhelníku není ani číslo $5$, ani číslo $7$:

  $$S\ge 2+3+4+6+8+9+10+12+14=68.$$

• Číslo $7$ v trojúhelníku je, ale číslo $5$ ne:

  $$S\ge 2+3+4+6+7+8+9+10+k\cdot 7\ge 49+14=63.$$

Rozebrali jsme všechny situace, které mohou nastat, takže zbývá ukázat, že trojúhelník umíme doplnit čísly se součtem $59$. Pro to existují dvě řešení zobrazená na obrázcích. Nejmenší možný součet je tedy $59$.

Výsledek:

$93$

Předpokládejme, že obsah domečku je $3$ (to nastane, pokud je délka strany čtverce $1$). Potom je v prvním nakresleném domečku 8 trojúhelníků s obsahem $\frac{1}{4}$, dále 8 trojúhelníků s obsahem $\frac{1}{2}$ a konečně 3 trojúhelníky s obsahem 1. To je 19 trojúhelníků.

Přikreslí-li Anička druhý domeček, pak na obrázku přibude stejný počet trojúhelníků jako předtím, a navíc ještě dva trojúhelníky s obsahem $1$, které zasahují do prvního i druhého domečku. Dohromady tedy přibude 21 trojúhelníků.

Počínaje třetím domečkem to pak bude 22 trojúhelníků – 21 stejných jako v druhém domečku, a navíc ještě jeden trojúhelník s obsahem 4, který zasahuje do tří domečků.

Víme, že $2021-19-21=1981$ a $1981=90\cdot 22+1$, takže Anička musí nakreslit $2+90+1=93$ domečků.

Výsledek:

$\frac{15}{4}$

Poměr obsahu trojúhelníků $\mathit{BEG}$ a $\mathit{BEF}$ je $4:3$. Vzhledem k tomu, že oba trojúhelníky sdílí stranu $\mathit{BE}$, tak jejich výšky na tuto stranu musí být také v poměru $4:3$. Dále víme, že $△\mathit{ABG}$ a $△\mathit{CDF}$ mají stejný obsah, takže

Výsledek:

$6375$

Matěj může odstřihnout proužek liché šířky, pokud součet šířek proužků je menší než délka kratší strany, tj.

Víme, že

takže 89 je šířka posledního možného proužku liché šířky. Podobně, aby Matěj mohl odstřihnout proužek sudé šířky, musí platit, že

Zřejmě,

tedy proužek šířky $90$ je poslední proužek sudé šířky. Zbývající obdélník má tedy obsah $(2100-2025)\cdot (2155-2070)=75\cdot 85=6375$.

Výsledek:

$\frac{10}{3}$

Označme rozměr $x$ a hledanou šířku $w$ jako na obrázku, který znázorňuje horizontální projekci. Protože mají oba prstence stejný průměr, je délka $x$ také výška od bodů dotyku obou prstenců po nejnižší bod vertikálního prstence. Platí tedy $1+x=w$. Pak

Výsledek:

$29030400$

Polynom můžeme napsat ve tvaru

kde $b_1,b_2,\dots ,b_{14}$ jsou po dvou různá celá čísla. Vedoucí koeficient je pak roven $c$, takže $c$ je kladné celé číslo. Dosazením do tvaru výše vidíme, že hodnota polynomu v 0 je rovna

Vzhledem k tomu, že chceme tuto hodnotu minimalizovat, volme $c$ nejmenší možné, tj. $c=1$. Chceme-li minimalizovat součin kořenů, musíme je brát co nejblíž 0, tj. $1,-1,2,-2\dots$ Nakonec musíme pamatovat na to, že potřebujeme sudý počet záporných kořenů, protože minimalizovaný součin má být kladný. Výsledek je tedy

Výsledek:

$8783$

Mezi čísly $1$ a $2021$ je dohromady $9$ jednociferných, $90$ dvojciferných, $900$ trojciferných čísel a $2021-1000+1=1022$ čtyřciferných čísel. Celkem tedy Lenka napíše

Na každou cifru bude potřebovat alespoň jeden tah a na cifry $4$, $5$ a $7$ bude potřebovat ještě jeden navíc. Stačí nám tedy určit počet cifer $4$, $5$ a $7$. Všimněme si, že číslo $2021$ neobsahuje ani jednu z těchto cifer, takže stačí uvažovat pouze čísla do $2020$ včetně.

Pojďme nejdříve spočítat, kolikrát se v těchto číslech vyskytuje cifra $4$. Desetina všech napsaných čísel, tj. $202$, má na místě jednotek cifru $4$. Na pozici desítek se čtyřka vyskytuje v desetině čísel od $1$ do $2000$, ale v číslech od $2001$ do $2020$ nikdy – to dává dohromady $200$ čísel. Na pozici stovek ji pak rovněž najdeme $200$krát. Dohromady je tedy čtyřek $202+200+200=602$.

Stejná úvaha platí pro cifry $5$ a $7$. Lenka tedy celkem napsala $6977$ cifer a na $3\cdot 602=1806$ z nich potřebovala dva tahy. Dohromady tudíž udělala $6977+1806=8783$ tahů.

Výsledek:

$3845$

Nechť $f(k)$ značí číslo na pozici $k$. Ze zadání víme, že $f(6)=6,f(7)=7,f(9)=2$. Dále podle pravidel pro vyplnění tabulky nutně dostáváme, že $f(13)=6$, $f(15)=7$ a $f(12)=2$.

Dále můžeme postupovat dvěma způsoby – dívat se na dvojice čísel a určit, kde se mohou nacházet, nebo se dívat na políčka a určit, která čísla v nich mohou být. Například, podíváme-li se na trojky, máme tři možnosti

Pokud by platilo, že $f(10)=f(14)=3$, pak $f(16)$ může nabývat pouze hodnoty 4, a to dále znamená, že $f(11)=4$. Nyní ovšem už nemůžeme do tabulky umístit osmičky.

V případě, že $f(4)=f(8)=3$, máme pro umístění pětek dvě možnosti $f(5)=f(11)=5$ nebo $f(10)=f(16)=5$. V obou případech pak nemáme kam umístit čtyřky.

Poslední možnost, která zbývá, je $f(1)=f(5)=3$, ze které nutně plyne, že $f(2)=f(11)=8$. Jediná možnost, jak potom doplnit tabulku je $f(4)=f(10)=5$, $f(3)=f(8)=4$ a konečně $f(14)=f(16)=1$.

Jediným řešením úlohy je $3845$.

Výsledek:

$5,7=\frac{57}{10}$

Můžeme si představit, že obrázek znázorňuje rovnoběžník $A{E}^{\prime }{D}^{\prime }F$ přeložený podél úsečky $\mathit{BC}$. Tuto tezi snadno ověříme: Označme obrazy bodů $D$, $E$ podle osy souměrnosti $\mathit{BC}$ jako $D^{\prime }$, $E^{\prime }$. Pak $|\sphericalangle \mathit{CB}{E}^{\prime }|=65^{\circ }$, a protože $50^{\circ }+65^{\circ }+65^{\circ }=180^{\circ }$, je $|\sphericalangle \mathit{AB}{E}^{\prime }|=180^{\circ }$. Díky dvojicím rovnoběžných úseček je i $|\sphericalangle \mathit{FC}{D}^{\prime }|=180^{\circ }$. Shodnost úhlů $|\sphericalangle \mathit{BAF}|=|\sphericalangle \mathit{CDE}|$, tedy i $|\sphericalangle \mathit{BAF}|=|\sphericalangle C{D}^{\prime }{E}^{\prime }|$, již potvrzuje, že $A{E}^{\prime }{D}^{\prime }F$ je skutečně rovnoběžník.

Z rovnoběžností úseček a ze střídavých a protějších úhlů plyne, že $|\sphericalangle \mathit{BGC}|=50^{\circ }$. Trojúhelník $\mathit{BGC}$ je tedy rovnoramenný s $|\mathit{BG}|=|\mathit{CG}|=5$.

Nyní již můžeme spočítat hledanou délku strany šestiúhelníku:

Výsledek:

$36$

Uvažujme obdélník $4\times 2$. Jak je vidět z prvních dvou obrázků, vystřelí-li Fíla pouze jednou do takového obdélníku a nezasáhne, tak nemá jistotu, že tam letadlová loď není. Musí vystřelit dvakrát – do každého řádku jednou (příklad je na třetím obrázku). Herní plochu umíme bez překrývání pokrýt $18$ takovými bloky a na každý z nich potřebuje Fíla dva výstřely. Dohromady tedy musí vystřelit alespoň $36$krát.

Zároveň tato strategie zaručuje, že $36$ střel stačí, aby Fíla Matějovu loď zasáhl (viz následující obrázek).

Výsledek:

$13$

Protože je $\mathit{ABC}$ ostroúhlý, platí $h_b<a$ a $h_c<a$. Pokud ale má být obsah $S=\frac{1}{2}a{h}_a$ maximální, musejí být obě výšky $h_b$ a $h_c$ co nejdelší (můžeme si ověřit, že pokud se budeme držet podmínky $h_b<a$ a délku výšky $h_c$ necháme stejnou, prodloužením výšky $h_b$ se nutně prodlouží i $h_a$). Pak musí platit $h_b=h_c=a-1$, a $\mathit{ABC}$ je tedy rovnoramenný.

Označme střed strany $\mathit{BC}$ jako $M$ a patu výšky $h_c$ jako $C_0$. Z Pythagorovy věty pro podobné pravoúhlé trojúhelníky $\mathit{ABM}\sim \mathit{CB}{C}_0$ spočítáme

Protože je $101,4$ racionální číslo a $2a-1$ je zjevně liché, musí být číslo $2a-1$ druhou mocninou lichého čísla, například $2a-1={(2k+1)}^2$ pro nějaké celé číslo $k\ge 0$. Dosazením zjistíme, že $a=\frac{{(2k+1)}^2+1}{2}\in \{1,5,13,25,41,\dots \}$. Vyzkoušíme prvních pár čísel a uvědomíme si, že s rostoucím $a$ roste i obsah. Snadno pak najdeme správnou odpověď $a=13$.

Výsledek:

$3099$

Čísla seřazená podle velikosti označme postupně $101=n_1,n_2,\dots ,n_{1000}$. Představme si nejprve, že rozdíl každých dvou po sobě jdoucích čísel je roven $2$. Potom

Rozdíl mezi zadaným součtem čísel na tabuli a minimálním součtem čísel, která splňují podmínku na rozdíl ze zadání, je $100500=20100\cdot 5$. Zvětšíme-li rozdíl $n_{i+1}-n_i$ z dvou na sedm, pak se součet všech čísel zvýší o $(1000-i)\cdot 5$ a poslední číslo se zvýší o $5$.

Z toho plyne, že pro maximalizaci $n_{1000}$ musí být rozdíl $7$ mezi čísly na co největších indexech, aby se součet zvětšoval co nejpomaleji (za předpokladu, že se pak dopočítáme na správný součet). Naštěstí je číslo $20100$ dělitelné třemi, tedy když zvětšíme rozdíly čísel $n_{i+1}-n_i$ pro $i=800,\dots ,999$ na $7$ místo $2$, dostaneme požadovaný součet. Největší možné napsané číslo pak je

Výsledek:

$29292929292$

Nejprve uvedeme řešení, které nevyužívá znalost kritéria dělitelnosti jedenáctkou; jednodušší řešení založené na této podmínce je uvedeno v posledním odstavci.

Všimněme si nejdříve, že $100$ dává po dělení $11$ zbytek $1$. To znamená, že pokud číslo vynásobíme stem, nezmění se jeho zbytek po dělení $11$. Nyní předpokládejme, že kladné číslo v desítkovém zápisu obsahuje dvě stejné číslice $a$ za sebou. Pak lze toto číslo napsat ve tvaru $x\cdot 10^{n+2}+11\cdot a\cdot 10^n+y$ pro vhodná celá čísla $x$, $y$ a $n$.

Zřejmě platí, že číslo $x\cdot 10^n+y$ je menší než předchozí číslo, jeho počet cifer má stejnou paritu a zároveň dává stejný zbytek po dělení $11$, protože vzniklo z předchozího součtu podělením prvního členu $100$ a vyškrtnutím druhého členu, který je dělitelný $11$. Z toho plyne, že hledané číslo neobsahuje dvojici po sobě jdoucích dvojek nebo devítek, protože jejich vyškrtnutím bychom dostali menší číslo s kýženými vlastnostmi.

Nyní budeme jednoduše zkoušet delší a delší čísla tvaru $2929\dots 292$ a $9292\dots 929$, než najdeme nejmenší takové číslo dělitelné $11$.

Řešení je ještě jednodušší, pokud si pamatujeme pravidlo dělitelnosti $11$: číslo je dělitelné $11$ právě tehdy, když rozdíl součtu cifer na lichých a sudých pozicích je dělitelný $11$. Z toho je okamžitě vidět, že vyškrtnutím dvou po sobě jdoucích stejných cifer se nezmění dělitelnost $11$. Když pak dále uvažujeme čísla, v nichž se střídají dvojky a devítky, tak ta jsou dělitelná $11$, pokud výrazy $2n-9(n+1)$ (pro čísla začínající devítkou) nebo $9n-2(n+1)$ (pro čísla začínající dvojkou) jsou dělitelné $11$. V obou případech je nejmenší takové $n$ rovno $5$. Kandidáti na nejmenší číslo jsou proto $29292929292$ a $92929292929$. Vybereme to menší z nich.

Výsledek:

$\frac{3+\sqrt{5}}{2}\doteq 2,61803$

Všimněme si, že pětiúhelníky $p$ a $q$ se na sebe zobrazí ve stejnolehlosti se středem $F$. Tímto bodem také prochází spojnice obou dvojic nejvzdálenějších vrcholů, z nichž jsme si jednu vybrali a označili ji písmeny $X$ a $Z$.

Platí, že vnitřní úhel při vrcholu pravidelného pětiúhelníku má $108^{\circ }$ a úhlopříčka pětiúhelníku vedená z tohoto vrcholu dělí tento úhel v poměru $2:1$. Z toho plyne, že $|\sphericalangle \mathit{FAZ}|=|\sphericalangle \mathit{FZA}|=36^{\circ }$, takže trojúhelník $\mathit{AFZ}$ je rovnoramenný a

Protože mají všechny úhlopříčky v pravidelném pětiúhelníku stejnou délku, platí $|\mathit{XF}|=|\mathit{AE}|$. Použitím kosinové věty v rovnoramenném trojúhelníku $\mathit{AFE}$ získáme, že

Nakonec spočítáme, že

Výsledek:

$281$

Rovnici přepíšeme do tvaru

Z toho plyne, že $a$ dělí součin $\mathit{bc}$. Protože všechna tři čísla jsou prvočísla, musí nutně platit $a=b$ nebo $a=c$. V prvním případě dostaneme, že

Z poslední rovnice dopočítáme jediné prvočíselné řešení $(2,2,197)$. V druhém případě dostaneme

a z toho pak další dvě prvočíselná řešení $(47,5,47)$ a $(37,7,37)$. Hledaný součet je $197+47+37=281$.

Výsledek:

$\frac{21}{40}$

Označme destinace podle Alčina očíslování jako $A_1,A_2,\dots ,A_{10}$. Na dovolenou Alča s Jirkou vyrazí právě tehdy, Jirka přiřadí jedno z čísel $1$ až $3$ některé destinaci z trojice $A_1,A_2,A_3$ a zbylá dvě některé destinaci z $A_4,A_5,\dots ,A_{10}$. Šance, že se mu to náhodným očíslováním povede, je

Výsledek:

$-2$

Všimněme si, že polynom $p(x)$ můžeme napsat ve tvaru

kde druhý člen je kladný, takže jediný reálný kořen tohoto polynomu je $x=\frac{-b}{a}.$ Navíc víme, že $q(x)$ má dvojný kořen, takže platí

Protože $a$ i $b$ jsou kladná čísla, dostáváme $b=2a$. Dohromady vidíme, že součet kořenů je

Výsledek:

$312$

Nejprve zdůvodníme, proč můžeme předpokládat, že $n<p$ a že $5$-periodický desetinný rozvoj $\frac{n}{p}$ začíná hned za desetinnou čárkou: Kdykoli je totiž rozvoj $\frac{n}{p}$ jen posléze periodický, můžeme posunout desetinnou čárku vynásobením čísla $n$ vhodnou mocninou $10$. Pokud je potom $n\ge p$, najdeme $n^{\prime }<p$ splňující $n=\mathit{kp}+n^{\prime }$. Volbou $n^{\prime }$ místo $n$ pak „vymažeme“ část před desetinnou čárkou.

Pokud je $0,\overline{\mathit{ABCDE}}$ periodický desetinný rozvoj $\frac{n}{p}$, pak $99999\cdot \frac{n}{p}=10^5\cdot \frac{n}{p}-\frac{n}{p}=\mathit{ABCDE}$ je celé číslo. Protože $n<p$ a $p$ prvočíslo, vyplývá z toho, že $p\mid 99999$, neboli $p\mid 3^2\cdot 41\cdot 271$. Jak $\frac{1}{3}$, tak i $\frac{2}{3}$ mají nejkratší periodu délky $1$, ale $\frac{1}{41}=0,\overline{02439}$ a $\frac{1}{271}=0,\overline{00369}$ jsou požadovaného tvaru. Výsledek je tedy $41+271=312$.

Výsledek:

$5680$

Očíslujme jazyky čísly $1$ až $5$. Následně symbolem $A_i$ označme množinu všech možných přiřazení jazyků, ve kterých je $i$-tý jazyk srozumitelný pro všechny – formálně vzato jde o množinu uspořádaných čtveřic neuspořádaných trojic jazyků, v nichž každá trojice obsahuje $i$-tý jazyk. Úloha se nás pak ptá po $\left|{\bigcup }_{i=1}^5{A}_i\right|$, což spočteme pomocí principu inkluze a exkluze. Velikost jedné množiny $A_i$ určíme snadno: Máme vybraný jeden „společný“ jazyk (ten $i$-tý) a celkem ${\left(\genfrac{}{}{0.0pt}{}{4}{2}\right)}^4=6^4$ možností, jak všem vybrat zbylé dva – $6$ způsobů pro každého člověka, přičemž výběr u dvou různých lidí je nezávislý. Těchto množin je $5$.

Následně spočítáme velikosti průniků $A_i\cap A_j$. Máme vybrané dva společné jazyky ($i$-tý a $j$-tý) a celkem $3^4$ způsobů, jak doplnit pro každého člověka zbylý jazyk. Těchto množin je tolik, kolika způsoby můžeme vybrat dva společné jazyky, tedy $10=\left(\genfrac{}{}{0.0pt}{}{5}{2}\right)$.

Nakonec se zaměříme na průniky trojic množin $A_i\cap A_j\cap A_k$. Tři společné jazyky můžeme vybrat $10=\left(\genfrac{}{}{0.0pt}{}{5}{3}\right)$ způsoby, a pro každý z nich je velikost daného průniku rovna jedné. Průniky více než tří $A_i$ jsou nulové. Z principu inkluze a exkluze tedy můžeme psát

což je hledané řešení úlohy.

Výsledek:

$\frac{65}{98}$

Pokud $\frac{a}{b}$ je menší než $\frac{2}{3}$, pak $\frac{a+2}{b+3}$ je větší než $\frac{a}{b}$ a menší než $\frac{2}{3}$. Stačí tedy vyzkoušet zlomky s jmenovateli $98$, $99$ a $100$. Řešením je největší ze zlomků $\frac{65}{98}$, $\frac{65}{99}$ a $\frac{66}{100}=\frac{33}{50}$. Porovnáním určíme, že

Výsledek:

$130$

Celkový povrch objektu je roven součtu povrchů jednotlivých černých kostek bez dvojnásobku počtu všech stěn, kterými se některé dvě černé kostky dotýkají. Podle orientace kostek rozlišujeme tři typy dotyků. Označme je předo-zadní, horno-dolní a pravo-levý. Třetí zmiňovaný typ dotyku se musí promítnout do obou obrázků, a to dvojicí horizontálně sousedících černých čtverečků ve stejných dvou sloupcích. Projdeme-li obrázky sloupec po sloupci, zjistíme, že takový dotyk nemohl nastat.

Pokud se kostky dotýkají předo-zadně, pak se na prvním obrázku promítnou do téhož sloupce a budou sdílet vodorovnou hranu, a na druhém obrázku se jeví jako jeden černý čtvereček. Na prvním obrázku máme v prvním sloupci tři čtverce, které sdílejí dvě hrany. Vzhledem k tomu, že na druhém obrázku je v tomto sloupci jediný černý čtverec, připadají na ně celkem dva předo-zadní dotyky; v dalších sloupcích už první obrázek takový dotyk neumožňuje. Horno-dolní dotyk se od předo-zadního liší jen tím, že si obrázky prohodí role. Stejnou úvahou jako v případě předo-zadního dotyku proto dojdeme k tomu, že i tyto dotyky jsou dva (tentokrát v pátém sloupci).

Plocha objektu je tedy $6\cdot 23-2\cdot 4=130$.

Výsledek:

$204$

Víme, že $720=2^4\cdot 3^2\cdot 5$. Podíváme-li se na exponenty jednotlivých prvočísel, tak ty v postupném rozkladu tvoří neklesající posloupnost, jejíž součet je roven exponentu tohoto prvočísla v čísle $720$. Pro prvočíslo dvě máme možnosti $(1,1,1,1)$, $(1,1,2)$, $(2,2)$, $(1,3)$, $(4)$ a všechny předchozí s přidáním libovolně mnoha nul na začátek. Pro trojku máme podobně možnosti $(1,1)$ nebo $(2)$ a pro pětku pouze $(1)$. V obou případech můžeme opět na začátek přidat několik nul. Libovolná kombinace těchto posloupností nám dává platný rozklad exponentů jednotlivých prvočísel, pokud všechny posloupnosti doplníme na délku nejdelší z nich nulami na začátku. Celkem tedy máme $5\cdot 2\cdot 1=10$ postupných rozkladů čísla $720$ a aritmetický průměr vedoucích členů je

Výsledek:

$9450$

Označme $n$, $a$, $b$, $o$, $j$ po řadě počty kamenů s písmeny $N$, $A$, $B$, $O$, $J$. Hledáme pětice $(n,a,b,o,j)$ s

Mocniny každého prvočísla mohou být nezávisle rozděleny mezi čísla $n$, $a$, $b$, $o$, $j$ a různá rozdělení odpovídají různým pěticím. Například pro prvočíslo $2$ potřebujeme rozdělit $5$ objektů do pěti krabiček. To lze udělat $\left(\genfrac{}{}{0.0pt}{}{9}{4}\right)$ různými způsoby, neboť ekvivalentně si můžeme vybrat, která z $9$ věcí je objekt a která je rozdělovač mezi krabičkami. Obdobně pro $3$ existuje $\left(\genfrac{}{}{0.0pt}{}{6}{4}\right)$ různých způsobů a pro $5$ jich je $\left(\genfrac{}{}{0.0pt}{}{5}{4}\right)$. Celkem tedy existuje

vhodných sad Scrabboje.

Výsledek:

$4978$

Předpokládejme, že $n$ je aspoň $2021$. Potom po vydělení $4^{2021}+4^n+4^{3500}$ číslem $4^{2021}={\left(2^{2021}\right)}^2$ dostaneme opět čtverec

kde $m=n-2021$. Tento výraz je druhou mocninou čísla většího než $2^m$. Můžeme ho tedy zapsat jako

pro nějaké kladné celé číslo $x$. Potom $x\cdot 2^{m+1}+x^2=2^{2958}+1$. Levá strana roste s rostoucími $m$ i $x$, zatímco pravá strana je konstantní. Řešení s největším $m$ má tedy nejmenší $x$. Pro $x=1$ dostaneme $m=2957$ a $n=m+2021=4978$. Náš počáteční předpoklad, že největší $n$ je nejméně $2021$, je tedy potvrzen. Řešením je $n=4978$.

Výsledek:

$1021616$

Definujme polynom

a všimněme si, že všechny nenulové koeficienty jsou kladné a že v žádném členu není $x$ v první mocnině. Tvrdíme, že tyto koeficienty odpovídají skoro všem mocninám $x^k$, kde

Určitě však $k\ne 1$ a $k\ne S-1$, protože žádná závorka neobsahuje $x$, takže nejnižší nenulová mocnina $x$ je $x^2$ a druhá nejvyšší mocnina je $x^{S-2}$.

Nyní dokážeme, že všechny ostatní mocniny výše jsou v polynomu přítomny s kladným koeficientem, neboli že nejmenší číslo $m$ větší než $1$, které nelze zapsat jako součet nějaké podmnožiny čísel z množiny $\{2,3,\dots ,2021\}$, je $S-1$. Tvrzení jsou ekvivalentní, protože platí, že ve výsledném součinu jsou právě ty mocniny $x$, které lze napsat jako součin nějaké podmnožiny mocnin $x$ v závorkách. Zřejmě $m\ge 3$.

Tvrdíme, že

pro nějaké $k=2,3,\dots ,2021$. V opačném případě umíme $m-1$ zapsat jako součet čísel z podmnožiny $M$ množiny $\{2,3,\dots ,2021\}$ a navíc existuje číslo o jedničku větší než nějaké číslo z $M$, které v množině $M$ není a není větší než 2021. Vyměníme-li tato dvě čísla, pak součet čísel z $M$ je roven $m$, což je spor.

Navíc platí, že $k\le 3$, jinak

je způsob, jak vyjádřit $m$. To znamená, že $m=1+3+4+\dots +2021=S-1$. Tedy $Q(x)$ má $\frac{S}{2}+1$ kladných koeficientů u sudých mocnin $x$ a $\frac{S}{2}-2$ kladných koeficientů u lichých mocnin $x$. Původní polynom má znaménka koeficientů u lichých mocnin opačná než $Q(x)$, takže má právě $\frac{S}{2}+1=1021616$ kladných koeficientů.

Výsledek:

$26550$

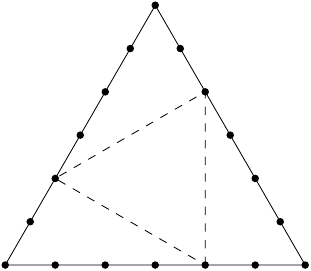
Všimněme si, že libovolná cesta délky $1$ z bodu $(x,y,z)$ nás dovede do bodu, který se oproti němu bude lišit právě v jedné souřadnici, a to o $\pm 1$. Abychom se dostali z bodu $(0,0,0)$ do $(4,4,4)$, musíme tedy projít alespoň čtyři hrany v kladném směru osy $x$, alespoň čtyři v kladném směru osy $y$ a alespoň čtyři v kladném směru osy $z$.

Půjdeme-li po hraně v opačném než kladném směru, pak nejdeme po nejkratší cestě, protože za každou takovou hranu pak musíme jít hranou v opačném směru a tyto dvě hrany nás v součtu nikam neposunou. Nejkratší cesta má tedy dvanáct hran (všechny procházíme v kladném směru některé z os). Pro určení počtu takových cest můžeme nejdříve vybrat, které z těchto dvanácti hran povedou ve směru osy $x$, a ze zbylých osmi pak čtyři hrany, které povedou ve směru osy $y$, tj.

Nyní zbývá určit počet cest, které prochází bodem $(2,2,2)$. Ze symetrie víme, že počet nejkratších cest vedoucích z $(0,0,0)$ do $(2,2,2)$ je roven počtu nejkratších cest z $(2,2,2)$ to $(4,4,4)$, což je na základě stejné argumentace jako výše