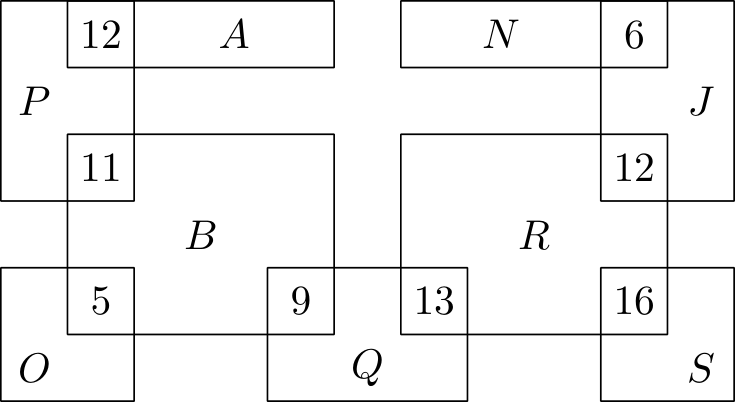
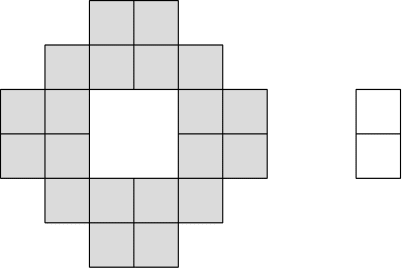
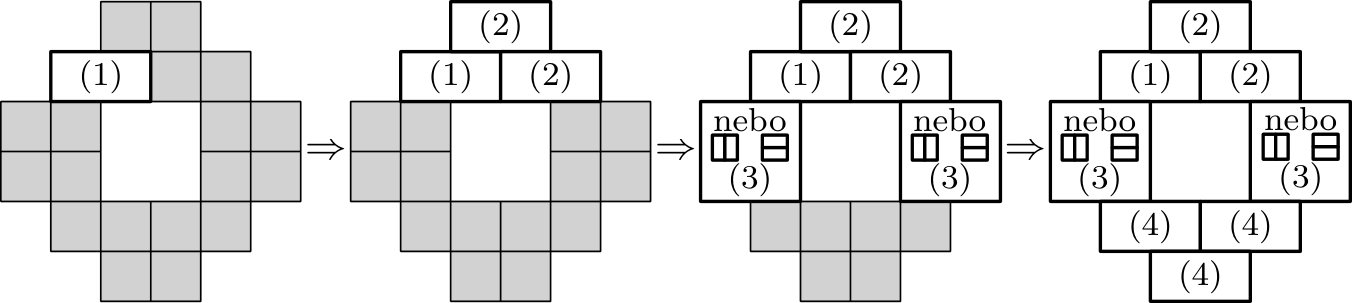
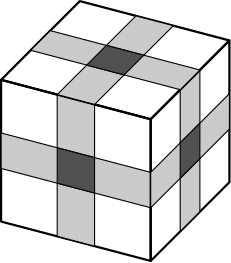
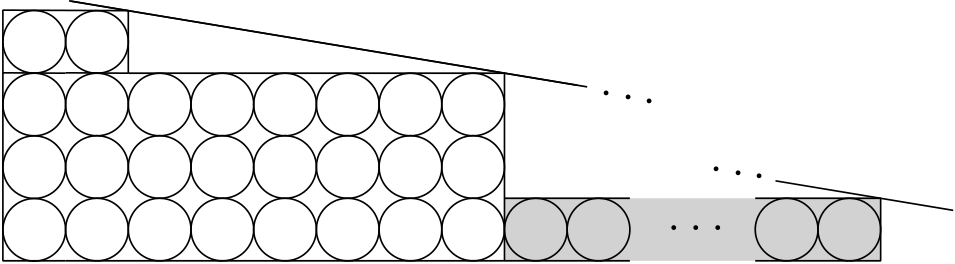
Nové matfyzácké koleje mají pater. V každém patře je jedna chodba a ze schodiště vedou vždy dvoje dveře, oboje přímo na tuto chodbu. Na každé chodbě se nacházejí čtyři pokoje, každý má svoje vlastní dveře a v každém žije jedna osoba. Na každé dveře včetně těch do chodby bude instalován právě jeden zámek a studentům budou rozdány klíče tak, aby byly splněny tyto podmínky:
- Každý má přístup do svého pokoje, ale ne do pokoje nikoho jiného.
- Každý má přístup na chodbu ve svém patře.
- Je možné, že někdo má i přístup na chodby v jiných patrech.
Každý typ zámku k sobě má jednoznačně přiřazený klíč a je možné jej odemknout jen tímto klíčem a jeho kopiemi. Stejný typ zámku může být použit na vícero dveřích a od každého klíče je možno vyrobit a rozdat jakýkoli počet kopií. Člověk může vlastnit jakýkoli počet klíčů. Firma, která má celou záležitost na starosti, se snaží minimalizovat náklady na výrobu klíčů. Výroba nového klíče je stojí 3 eura, zatímco vytvoření kopie existujícího klíče jen 2 eura. Pokud trváme na dodržení uvedených podmínek, kolik nejméně je nutno za klíče celkem zaplatit?Řešení
Výsledek:
Zjevně nedává smysl, aby některý student měl více než dva klíče, a to jeden od svého pokoje a jeden, kterým se dostane do chodby na svém patře. Nyní v následujících třech odstavcích zdůvodníme, že můžeme předpokládat, že v každém patře bydlí právě jeden student, který si vystačí s jediným klíčem, jímž si odemkne svůj pokoj i jedny dveře na chodbě. Nikdo další pak už tento klíč mít nemůže (dostal by se k němu do pokoje), a proto ostatní tři ubytovaní na stejném patře používají pouze druhé chodbové dveře.
Předpokládejme, že jsme studentům rozdali klíče tak, aby byly splněny podmínky úlohy, ale přitom existuje patro, kde mají všichni studenti dva klíče, které potřebují. Ukážeme, že umíme změnit situaci na tomto patře tak, aby jeden student měl jen jeden klíč, a přitom byla celková cena klíčů stejná nebo nižší. Na tomto patře jistě jedny z dveří na chodbu používají maximálně dva ze čtyř studentů; označme tyto dveře a ony studenty a případně . (Student nemusí existovat; a pokud dveře nevyužívá nikdo, stačí jako označit libovolného ze čtyř studentů.) Upravíme zámky na dveřích následujícím způsobem: na chodbové dveře a dveře od pokoje studenta instalujeme úplně nové totožné zámky. Student tak nyní potřebuje pouze jeden originální klíč za eura, kdežto předtím jeho klíče stály minimálně eura. Cenu na výrobu jsme tak snížili alespoň o 1 euro.
Nyní se ovšem ještě musíme postarat o studenta , pokud existuje. Místo klíče k mu vytvoříme kopii klíče ke druhým chodbovým dveřím na tomto patře. Tím se cena jeho klíčů jistě nezvýšila. Student má nyní novou sadu dvou klíčů (jeden mu byl vyměněn), která by se teoreticky mohla shodovat se sadou nějakého studenta z jiného patra. Pokud by tomu tak bylo, situaci opět napravíme instalací nového zámku na dveře od pokoje studenta . Tím zaplatíme maximálně o 1 euro navíc za nový klíč místo kopie.
Jelikož se celková cena potřebných klíčů během tohoto procesu určitě nezvedla, můžeme skutečně u optimálního řešení předpokládat, že jeden student z každého patra má jen jeden klíč, jak jsme uvedli v prvním odstavci.
Tím jsme problém zredukovali na úkol minimalizovat cenu klíčů v situaci, kdy máme budovu se 160 patry, jedněmi hlavními dveřmi na každou chodbu a třemi pokoji na každém patře. Nechť je v této situaci rozdáno různých typů klíčů, očíslovaných . Každý student dostane jeden klíč ke svému pokoji a jeden k hlavním dveřím na patře. Tyto dva klíče nemohou být stejného typu (i když by pak bylo možné použít jen jeden a tím snížit cenu): Kdyby totiž byly stejné, pak by zbylí dva studenti z daného patra buď mohli vniknout do příslušného pokoje, nebo by se nebyli schopni dostat do chodby na svém patře. Také nemohou žádní dva studenti mít stejnou dvojici typů klíčů, protože pak by se byli oba schopni dostat přesně na tatáž místa, což neodpovídá zadání. Každý student proto dostane jiný z párů typů klíčů. Protože studentů, kterým rozdáváme dva klíče, je celkem , získáváme dolní odhad pro z nerovnosti
Pro celé číslo to znamená . Nyní ukážeme, že lze použít přesně typů klíčů. Toho dosáhneme tak, že rozdělíme 160 pater do 32 skupin po 5 patrech (a tedy 15 studentech). Přiřazení klíčů pak provedeme takto (první klíč je od dveří do chodby a druhý od dveří do pokoje):
- V první skupině rozdáme 15 studentům postupně páry typů klíčů .
- Ve druhé skupině rozdáme páry .
- Takto pokračujeme, takže 31. skupina dostane páry .
- A poslední, 31. skupina dostane páry .
Snadno vidíme, že toto rozdělení splňuje uvedené podmínky. Proto je nejmenším možným počtem typů klíčů, které (po první redukci) potřebujeme; a ve chvíli, kdy všem studentům rozdáváme po dvou klíčích, je cena určena skutečně jen počtem použitých typů. Při výrobě klíčů pro studentů se dvěma klíči tedy nejprve vyrobíme originálů a následně kopií, abychom jim celkem rozdali klíčů.
Když k tomu připočítáme dalších originálů pro studenty, kteří budou mít jen jeden klíč, je dohromady nutno vyrobit různých originálů. Finální cenu proto spočteme jako .