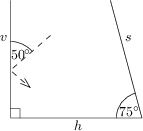
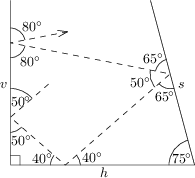
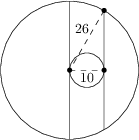
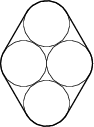
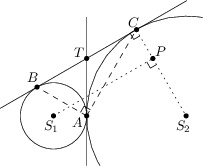
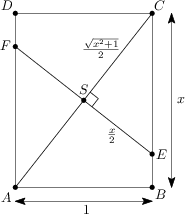
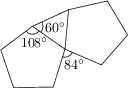
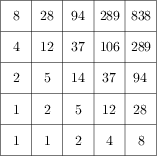
Problems and solutions

Answer:

2

The volume of the original blockstone was $2\cdot 3\cdot 4=24$. Since all three cubes have the same volume, it equals $\frac{24}{3}=8$. As the volume of a cube is the third power of its sidelength, we conclude that the sidelength of the three golden cubes is $\sqrt[3]{8}=2$.

Answer:

11

The total number of people drinking alcohol was $25+19-12=32$ (we added the numbers of people drinking beer and people drinking champagne and subtracted the number of those drinking both beverages, since we counted them twice). All the others drank juice only, so there were $43-32=11$ such people.

Answer:

$2:1$

Denote by $k$ the amount of caffeine for one hour. Then black tea contains $k$, coffee contains $4k$ and our goal is to mix $2k$ into one cup. If we fill a fraction $x$ of a cup with tea and the remainder $1-x$ with coffee into one cup, the amount of caffeine in the mixture satisfies $x\cdot k+(1-x)\cdot 4k=2k$. This yields $x=2∕3$ and hence the desired ratio is

Answer:

$80^{\circ }$

We sketch the trajectory of the light ray into a picture and compute angles in the resulting triangles. The angle of the first reflection from $v$ is $50\circ$ from the last assumption. We know that the sum of angles in a triangle is $180\circ$ and $v$ is perpendicular to $h$. Therefore the angle of incidence on $h$ was $40\circ$, as was the angle of reflection. By the same reasoning, we infer that the angle of reflection from $s$ was $65\circ$. Next we recall that the sum of angles in a quadrilateral is $360\circ$ and hence compute the desired value, i.e. $360\circ -90\circ -75\circ -(180\circ -65\circ )=80\circ$.

Answer:

4, 5, 3

Let $a$, $b$ and $c$ be the number of months in which 20, 16 and 25 spacecrafts were sold, respectively. Then $20a+16b+25c=235$. The right hand side is divisible by 5, so the left hand side has to be divisible by 5, too. Clearly, $20a+25c$ is a multiple of 5, hence $16b$ has to be a multiple of 5 as well. Since $5\nmid 16$, necessarily $5\mid b$. There are only three possibilities:

• $b=0$. Then $c=12-a$ and we get $20a+25(12-a)=235$ or $4a+60-5a=47$. Thus $a=13$, which is not possible as there are only twelve months altogether.
• $b=5$. Then $a=7-c$ and substitution gives $80+5c=95$. The solution is $a=4$, $c=3$.
• $b=10$. Then $c=2-a$ and $210-5a=235$, which is not possible.

Answer:

4

The longest chord is clearly the diameter of the larger circle, so its length is 52. The shortest is the one whose distance from the centre of the larger circle is the greatest. This distance can be at most 10, because the chord has to be tangent to the smaller circle. By the Pythagorean theorem, the length of the shortest chord is $2\cdot \sqrt{26^2-10^2}=48$, so the desired difference is $52-48=4$.

Answer:

1976

Let $10x+y$ be his age in 1999, where $x$, $y$ are digits. Since he was born in the 20th century, the sum of the digits of his year of birth is $1+9+(9-x)+(9-y)$, therefore $28-x-y=10x+y$ or $28=11x+2y$. Since $0\le x,y\le 9$, the only solution is $x=2$, $y=3$, hence he was born in $1999-23=1976$.

Answer:

$8+2\pi$

We can split the band into straight and curved parts. The curved parts together form a full turn, so their total length is $2\pi$. The length of each straight part is the same as the distance of the centers of the corresponding circles, which is 2. Thus the overall length is $8+2\pi$.

Answer:

2, 7, 17

Let $m$ be the number of legs of the middle bug, and let $b$ be number of Buggy’s legs. Then we have

or $b=5m-28$. As $m$ is also the median (i.e. the “middle value”), it has to be one of 6, 9, or $b$, so (by plugging into the last equation) we find that $b$ is one of 2, 7, or 17.

Answer:

198

Comparison of the units digit in the equality yields $A+B+C=C+f$ or $A+B=f$, where $f$ is $0$ or $10$; as $A$, $B$ are non-zero digits, only $A+B=10$ is possible. Similarly, the tens digit gives $A+B+C+1=B+10$ (the one on the left hand side is carried from units) or $A+C=9$. Finally, since we again carry only $1$ to the hundreds, we obtain $A=1$, thus $B=9$ and $C=8$.

Answer:

54

Let $x$ be the number of celestial objects at the beginning. The number of objects changes during the process in the following way:

After a bit of manipulation we obtain

Answer:

2019

If a number greater than 2014 can be written as a sum of two palindromes, then one of these palindromes needs to be at least 4 digits long. However, there are not many of these – namely $1001,1111,\dots ,1991,2002$ (and the rest is too large). We can write the numbers up to 2018 as $2015=1551+464$, $2016=1441+575$, $2017=1331+686$ and $2018=1221+797$.

Assume that 2019 can be decomposed in such a fashion; then one of the summands must have four digits. If the second summand had an even number of digits, their sum would be a multiple of 11, whereas 2019 is not. Thus we have $2019=\overline{1\mathit{AA}1}+\overline{\mathit{BCB}}$, where $A$, $B$ and $C$ are digits. From the units digit we see that $B=8$, so there is no carrying and either $A+C=1$ or $A+C=11$. The former would imply $\overline{1\mathit{AA}1}+\overline{8C8}<2000$, the latter $A+8+1=10$ (hundreds digit), so $A=1$ and $C=10$ which is a contradiction. Therefore the number we are looking for is 2019.

Answer:

4

Taking into account the well-known rule for divisibility by 11 the problem simplifies to determining for which digit $X$ there is no digit $Y$ (the units digit) such that $(X+Y)-3$ is divisible by 11. This further reduces to seeking $X$ such that $0<X+Y-3<11$ for all $Y$, which is satisfied only for $X=4$.

Answer:

$3.5$, $4$

The two smallest sums clearly are $a+b$ and $a+c$, hence $a+b=1$ and $a+c=2$. Similarly, the two largest sums are $c+d$ and $b+d$, so there are two cases:

• $a+d$ = 3, $b+c=4$: Then we have $2b=(a+b)-(a+c)+(b+c)=1-2+4$, so $b=1.5$, resulting in $a=-0.5$ and $d=3.5$.
• $b+c$ = 3, $a+d=4$: The same computation yields $b=1$, thus $a=0$ and $d=4$.

Answer:

40

Let $x$ and $y$ be Jack’s and Jill’s age, respectively. The first sentence says $x=2(y-(x-y))$, whence $3x=4y$. The second sentence then states $((x-y)+y)+((x-y)+x)=90$, implying $3x-y=90$. Therefore $x=40$ and $y=30$.

Answer:

820

It is well known that the $k$-th term of an arithmetic progression can be written as $a_k=a_1+(k-1)d=10+(k-1)d$. It follows that $a_2=10+d$ and thus

From the statement we know that $a_{a_2}=100$ and hence $100=10+9d+d^2$. The only positive solution of this quadratic equation is $d=6$. We infer that $a_k=4+6k$ and the rest is a straightforward computation: $a_3=4+18=22$, $a_{a_3}=a_{22}=4+132=136$, and finally $a_{a_{a_3}}=a_{136}=4+816=820$.

Answer:

97654320

Natali’s number is divisible by 20, so its units digit is 0 and its tens digit is even. However, it cannot be 4, 6 or 8, because then there would not be enough digits to complete an 8 digit number (in the light of the second condition), so it is 2. Further, we decide which of the digits $3,4,\dots ,9$ will be missing to ensure the divisibility by 9. Since $0+2+3+4+\cdots +9=44$, we omit the number 8. Finally, using the second condition, we conclude that Natali’s favourite number is 97654320.

Answer:

12

If we look at the resulting object from the front, we see the same number of squares as if we look from behind, similarly for other sides. Denote by $a$, $b$, and $c$ the number of squares seen from the front, the left, and above, respectively.

Assume that there are no unseen squares, then we get $2(a+b+c)=14$ (there are $14$ squares altogether). W.l.o.g. we may assume $a\le b\le c$. This leaves us with four possible triples $(a,b,c)$, namely $(1,1,5)$, $(1,2,4)$, $(1,3,3)$, and $(2,2,3)$. As the inequality $c\le \mathit{ab}$ must hold, only two possibilities remain: a block with dimensions $1\times 3\times 3$ and an “L”-shape, of which only the latter can be constructed from the given shape.

If there was an unseen square, there would have to be at least five squares visible from one side, which we have already ruled out.

Answer:

$(2,2)$

Let $d=\gcd (a,b)$. By considering the prime factorizations of $a$ and $b$, we can easily establish the (general) relation $\mathrm{lcm}(a,b)=\mathit{ab}∕d$, hence $\mathit{ab}=d+\mathit{ab}∕d$ or $(d-1)\mathit{ab}=d^2$. As $a,b\ge d$ and $d>0$, we infer that $a=b=d$ and $d-1=1$, thus $(a,b)=(2,2)$.

Answer:

256

Every path of the frog has to go through the square in the middle. On its way from this square the frog decides four times whether to jump directly up or diagonally, thus the number of ways from the middle up is $2^4=16$. The number of ways from the bottom row to the middle is the same as the number of ways from the middle downwards using the opposite moves (because of the symmetry of the diagram), so it is $16$ as well. Any two such subpaths may be joined in the middle square to form a full path, so the total number is $16^2=256$.

Answer:

0

Whenever Palo enters a vertex other than the first and the last one of his walk, he has to leave it along a previously unused diagonal. However, there is an odd number of diagonals incident at every vertex (namely five), therefore he cannot use all the diagonals incident to some vertex. We conclude that there is no such walk.

Answer:

4023

As $p$ passes through the points $(0,0)$ and $(2014,2019)$, each of its points $(x,y)$ satisfies $x∕y=2014∕2019$. Since $2014$ and $2019$ are coprime, the fraction $2014∕2019$ is in its lowest terms and $p$ does not pass through any vertex of a square in the grid other than $(0,0)$. Thus, $p$ crosses a new square with every intersected inner grid segment. “On its way” from $(0,0)$ to $(2014,2019)$, $p$ intersects $2013$ such horizontal and $\lfloor 2014^2∕2019\rfloor =2009$ vertical segments. If we add the corner square in which $p$ “starts”, we get $1+2013+2009=4023$ crossed squares in total.

Answer:

8, 9, 10, 11, 12

Every $n$-gon can be cut into $n-2$ triangles, hence the sum of interior angles is $(n-2)\cdot 180^{\circ }$. Thus we have $(n-2)\cdot 180^{\circ }=(n-1)\cdot 150^{\circ }+x$ or $n=x∕30^{\circ }+7$, where $0^{\circ }<x<180^{\circ }$ is an arbitrary convex angle. We conclude that $8\le n\le 12$.

Answer:

$60^{\circ }$

After multiplying the whole expression appropriately to get rid of fractions we obtain

so $a^2=b^2+c^2-\mathit{bc}$. Comparison with the law of cosines ($a^2=b^2+c^2-2\mathit{bc}\cos \alpha$) yields $\cos \alpha =\frac{1}{2}$ and $\alpha =60^{\circ }$.

Answer:

66, 132, 198, 55, 39, 117

The number 16 can be written as a sum of distinct primes in the following ways:

The first decomposition corresponds to the numbers of the form $2^a{3}^{b}11^c$ with $a$, $b$, $c$ positive integers; only $2\cdot 3\cdot 11=66$, $2^2\cdot 3\cdot 11=132$ and $2\cdot 3^2\cdot 11=198$ are less or equal $200$. The second case yields $3\cdot 13=39$, $3^2\cdot 13=117$ and from the last one we get $5\cdot 11=55$.

Answer:

3

The line segment $\mathit{AC}$ joins the midpoints of $\mathit{DB}$ and $\mathit{BI}$. Therefore its length must be $\mathit{AC}=\mathit{DI}∕2=2.5$. Similarly, $\mathit{CB}=\mathit{EF}∕2=2.5$ and $\mathit{AB}=\mathit{GH}∕2=3$. We see that $\mathit{ABC}$ is an isosceles triangle and its area can thus be computed by the Pythagorean theorem as

Answer:

2, 3, 5, 7, 23, 37, 53, 73, 373

One-digit strong primes (1SP) are 2, 3, 5 and 7.

Two-digit strong primes (2SP) are prime numbers obtained by joining two 1SP together, namely 23, 37, 53, and 73.

Let us now find the three-digit strong primes (3SP): By removing the first digit we get a 2SP and similarly by removing the last digit. Therefore, we seek two 2SP such that the second digit of one is the first digit of the other. Out of the possible candidates 237, 537, 737 and 373, only 373 is a prime.

Finally, we focus on the four-digit strong primes (4SP). After removing both the first and the last digit we need to obtain 3SP, i.e. 373, which is clearly impossible. Hence 4SP do not exist and neither do strong primes with more than 4 digits. To sum up, the only strong primes are 2, 3, 5, 7, 23, 37, 53, 73, and 373.

Answer:

6

Let $S_k$, $S_l$ and $S_m$ be the centres of the circles $k$, $l$, and $m$ respectively. Denote by $r$ the radius of the circle $m$. We know $S_k$, $S_m$ and the point where $m$ touches $k$ lie on one line, whence $S_k{S}_m=16-r$. Let $A$ be the point where the circle $m$ touches the line $p$. By symmetry we have $S_{k}A=S_{l}A=16∕2=8$. Clearly, $S_{m}A=r$ and the line $S_{m}A$ is perpendicular to $p$, so we can use the Pythagorean theorem in $△S_{k}A{S}_m$, yielding the equation $8^2+r^2={(16-r)}^2$ with the unique solution $r=6$.

Answer:

82

Firstly observe that the sum of distinct digits of any such number is 6. As 0 cannot occur among these numbers, we are looking for partitions of 6 into distinct positive integers; these are $6$ alone, $1+5$, $1+2+3$ and $2+4$. There are $6\cdot \left(\genfrac{}{}{0.0pt}{}{5}{2}\right)=60$ numbers with digits 1, 2, and 3, since there are six possible positions for digit 1 and then we choose two positions for digit 2 out of 5 remaining. Using similar elementary combinatorics, we compute that the partitions $6$, $1+5$ and $2+4$ provide $1$, $6$, and $\left(\genfrac{}{}{0.0pt}{}{6}{2}\right)=15$ valid numbers. Therefore, there are $60+1+6+15=82$ numbers satisfying the given condition.

Answer:

$1+\frac{\sqrt{6}}{2}$

When we decrease the radius of the containing sphere by 1, we obtain the circumscribed sphere $C$ of the regular tetrahedron $T$ formed by the centres of the given balls. Note that edges of $T$ are of the length $2$. Using the Pythagorean theorem, we discover that faces of $T$ have altitudes of the length $\sqrt{4-1}=\sqrt{3}$. Now we can calculate the length of the altitudes of $T$, once again by means of the Pythagorean theorem, obtaining $\sqrt{4-{(\frac{2}{3}\sqrt{3})}^2}=\frac{2}{3}\sqrt{6}$. It is well known (or we may employ the Pythagorean theorem for the third time) that the centre of $C$ divides the altitude with the ratio $1:3$, yielding the radius of $C$ as $\frac{\sqrt{6}}{2}$ and the desired value $1+\frac{\sqrt{6}}{2}$.

Answer:

99

Recall $x^2-y^2=(x-y)(x+y)$ and $x^3-y^3=(x-y)(x^2+\mathit{xy}+y^2)$. In order to achieve $\gcd ((x-y)(x+y),(x-y)(x^2+\mathit{xy}+y^2))=1$, we need $x-y=1$, i.e. $x=y+1$. Substituting for $y$, we search for $x$ such that $\gcd (2x-1,3x^2-3x+1)=1$. After subtracting $(2x-1)(x-1)$ from $3x^2-3x+1$, we get an equivalent condition $\gcd (2x-1,x^2)=1$. Suppose there exists a common prime divisor of $2x-1$ and $x^2$ and denote it $p$. Then $p\mid x$ and $p\mid 2x-1$, whence $p\mid x-1$. This contradicts $p>1$, so the assumption is false and $\gcd (2x-1,3x^2-3x+1)=1$ for any $x\ge 1$. Given that we have shown $x=y+1$, the desired pairs are $(2,1),(3,2),\dots ,(100,99)$. All in all there are 99 of them.

Answer:

4

One-digit numbers require $1+2+\cdots +9=45$ digits, two-digit numbers $2\cdot (10+11+\cdots +99)=2\cdot (\frac{99\cdot 100}{2}-\frac{9\cdot 10}{2})=9810$. Hence we reach 2014 digits while writing a two-digit number. Observe that we are asking for a digit in an even position, and considering one-digit numbers take up an odd length, we only need to know the value of the digit on tens place for the number that occupies the $2014$th position. The last written number is the least $n$ such that $45+2\cdot (10+11+\cdots +n)>2014$, which yields a rough estimate $40<n<50$, and so the last digit is 4.

Answer:

360

Let us list the first few values that can be obtained by $(t^2-1)$ for integer $t$: $0$, $3$, $8$, $15$, $24$, $35$, $48$, $63$, $80$, $99$, $120$, etc. We want to find two pairs with the same minimal product. Divine revelation yields $3\cdot 120=15\cdot 24=360$, which happens to be the smallest possibility actually: Should one of the factors be greater than 120, the product would exceed 360. Therefore we may confine ourselves to the factors listed above. Since at most one factor may be 3, we may concentrate only on the products without this factor smaller than 360, i.e. $8\cdot 8$, $8\cdot 15$, $8\cdot 24$, $8\cdot 35$, and $15\cdot 15$. These products, however, do not allow for an alternative factorization. Hence the smallest $N$ really is 360.

Answer:

24

Let $S_1$ be the centre of the smaller circle, $S_2$ the centre of the larger one and $T$ the point where the line $\mathit{BC}$ intersects the common tangent passing through $A$. Note that $\mathit{TC}=\mathit{TA}=\mathit{TB}$ (tangent lines). Thales’ theorem then implies that the triangle $\mathit{ABC}$ is right-angled and we obtain $A{B}^2+A{C}^2=B{C}^2$. Let us now translate the line segment $\mathit{BC}$ so that $B$ is moved onto $S_1$ and denote by $P$ the translated point $C$. Noting $\mathit{CP}=S_{1}B=1$, the Pythagorean theorem entails $B{C}^2=S_1{P}^2={(S_{1}A+S_{2}A)}^2-{(S_{2}C-\mathit{CP})}^2=12$, yielding the solution 24.

Answer:

43

Let $q$ be a prime. Then factors from $2014!$ divisible by $q$ are $q,2q,\dots ,\lfloor 2014∕q\rfloor q$. Denoting $m=\lfloor 2014∕q\rfloor$, we have $q^m\mid 2014!$. If $q>m$ then $q^2>\mathit{mq}$ and $q^{m+1}\nmid 2014!$, implying $q^q\nmid 2014!$, which is undesirable. Conversely, if $q\le m$, then clearly $q^q\mid 2014!$. Hence $p$ must be the largest prime satisfying $p\le \lfloor 2014∕p\rfloor$, i.e. $p^2\le 2014$, which results in $p=43$.

Answer:

$6\cdot 3^{2013}$

First we colour the bottom row arbitrarily, yielding $3\cdot 2=6$ possibilities. If a row is coloured $(a,b)$ then the next one can be $(b,a)$, $(b,c)$ or $(c,a)$. In other words, independently of choosing a colouring for a row, we have exactly three possibilities of how to colour the following one. That gives us $6\cdot 3^{2013}$ different colourings.

Answer:

$5^{84}{6}^{35}{7}^{90}$

Let us write $m=5^a{6}^b{7}^{c}d$ where $d$ is divisible by neither 5, 6 nor 7. In order for $5m$ to be a fifth power, we need 5 to divide $a+1$, $b$ and $c$. Likewise $6\mid a,b+1,c$ and $7\mid a,b,c+1$. The number $d$ has to be a fifth, sixth and seventh power at the same time; we are looking for the smallest integer, so we let $d=1$. The number $a$ is divisible by $42$ and $a+1$ by 5, therefore the smallest suitable $a$ is 84. We find $b=35$ and $c=90$ analogously. The smallest suitable $m$ turns out to be $5^{84}{6}^{35}{7}^{90}$.

Answer:

$\sqrt{\frac{1+\sqrt{5}}{2}}$

Label important points as in the picture. Since similar rectangles yield the same result, we may w.l.o.g. assume $\mathit{AB}=1$. The question is now to find $x=\mathit{BC}$. First note that $\mathit{EF}\perp \mathit{AC}$, as $\mathit{EF}$ is the axis of symmetry of $\mathit{AC}$. We can see that $\mathit{ES}=\mathit{FS}=\frac{x}{2}$ by symmetry. The Pythagorean theorem implies $\mathit{CS}=\frac{\sqrt{x^2+1}}{2}$. Triangles $\mathit{ABC}$ and $\mathit{ESC}$ are similar, hence we infer $\frac{x}{1}=\frac{\sqrt{x^2+1}}{x}$. This relation yields $x^4-x^2-1=0$ which, after substituting $z=x^2$, produces a unique non-negative solution $x=\sqrt{\frac{1+\sqrt{5}}{2}}$.

Answer:

17

Let $b$, $y$, $g$, and $r$ denote the number of blue, yellow, green, and red marbles, respectively. We have $\left(\genfrac{}{}{0.0pt}{}{20}{r}\right)$ different ways of placing the red marbles. There remain $20-r$ positions for the green marbles, hence $\left(\genfrac{}{}{0.0pt}{}{20-r}{g}\right)$ different ways of placing them, having placed the red ones. Similarly, the yellow marbles can be placed in $\left(\genfrac{}{}{0.0pt}{}{20-r-g}{y}\right)$ different ways after fixing the red and green marbles. The remaining blue marbles just fill in the void. So we seek the smallest $y+g+r$ such that

We can manipulate the expression to obtain

If $b\ge 18$, the numerator is at most $20\cdot 19=380$, so the number of ways is less than $1140$. For $b=17$ the number $1140$ can be attained via setting $y=3$, $g=0$, $r=0$.

Answer:

3, 4, 6, 12

Firstly observe that an equilateral triangle can be divided into four equilateral triangles by its midlines, a square can be divided into four squares and a regular hexagon into six triangles.

Consider a regular $n$-gon with $n\ne 3,4,6$. The internal angles of regular polygons with 3, 4, 5, and 6 vertices are $60^{\circ }$, $90^{\circ }$, $108^{\circ }$, and $120^{\circ }$, respectively. We have to “fill” the internal angle of the $n$-gon either using a smaller $n$-gon or two polygons with at most five vertices. However, the former option leaves us with an acute angle different from $60^{\circ }$, which cannot be filled.

Therefore, the internal angles of the $n$-gon have to be filled either with a triangle and a square or with a triangle and a pentagon. The corresponding interior angles are $150^{\circ }$ and $168^{\circ }$, i.e. $n$ is $12$ or $30$.

It is indeed possible to divide the regular dodecagon: We alternately put squares and triangles to the sides of the polygon and a hexagon to the middle.

On the other hand, such a division of a triacontagon does not exist; it would need to have a pentagon adjoined to every other side. Two such neighbouring pentagons would meet in a vertex with one angle equal to $60^{\circ }$, thus the angle on the other side would be $84^{\circ }$, which cannot be filled.

Answer:

838

For each square we compute the number of ways to reach it. There is only one way for the bottom left corner (empty sequence of moves). For every other square $S$ we take the following approach: Consider a sequence of moves ending in $S$ and exclude its last move; before this move, the rook was in a square $T$ either below or to the left of $S$. On the other hand, whenever the rook gets to a square $T$ below or to the left of $S$, by adding one move we obtain a way to reach $S$. Therefore if we know the numbers of ways to get to all such squares $T$, it suffices to sum up all these ways.

Thus we employ the following procedure: Firstly, we write $1$ to the bottom left corner of the board and then we repeatedly apply the rule “Find a square with all squares below and to the left filled in and fill it with the sum of these values.” The sought number is in the top right corner.

Answer:

$2$

The binomial theorem entails

We need to compute this expression modulo $1000$ and to take the first digit, so we may drop the terms grouped in the last brackets and proceed as

Answer:

$\frac{171}{512}$

Denote by $A$ the starting vertex and by $a_i$ the probability of the grasshopper being in the vertex $A$ after $i$ jumps (so $a_0=1$). We can find a recurrence relation for $a_{i+1}$ provided that $a_i$ is given: If the $(i+1)$-th jump of the grasshopper ended in $A$, then the previous jump did not and the grasshopper had to choose vertex $A$ out of the two possible ones, so

or, equivalently,

As $a_0=1∕3+2∕3$, we infer that

and thus

Answer:

4293

If Parsley spent a minute resting and in the following minute he cut trees, he would cut one tree less than if he firstly cut and then rested, but in neither case does his power change. Therefore, in order to maximize the number of trees cut, he begins with $r$ minutes of rest and proceeds with $60-r$ minutes of cutting for some $r$. The total number of trees cut is then

The maximum is attained if the term ${(r-6.5)}^2$ is lowest possible, i.e. for $r=6$ or $r=7$. In this case Parsley cuts $\frac{3}{2}\cdot 2862=4293$ trees.

Answer:

$6^{25}$

If $a=\sqrt{n_{a,1}}$ and $36∕a=\sqrt{n_{a,2}}$ for some $n_{a,1},n_{a,2}\in \mathbb{N}$, it follows $n_{a,1}{n}_{a,2}=36^2$. This observation lets us compute the desired product as follows:

Answer:

$1-{\left(\frac{5}{10}\right)}^{2014}-{\left(\frac{8}{10}\right)}^{2014}+{\left(\frac{4}{10}\right)}^{2014}$

We seek the probability that the product is divisible by both $2$ and $5$. Let us compute the probability of the complementary event: the probability of the product not being divisible by $2$ is $a={(5∕10)}^{2014}$ (all the factors have to be odd). Similarly, for the divisibility by $5$ we have $b={(8∕10)}^{2014}$ (there may be no $0$ or $5$), and the probability of not being divisible neither by $2$ nor $5$ is $c={(4∕10)}^{2014}$. The sought probability is $1-a-b+c$, since we have subtracted the probability of non-divisibility by $2$ and $5$ twice and thus we have to add it back.

Answer:

$-2002$

We rewrite the expression as

where $\lceil x\rceil$ denotes the smallest integer greater or equal to $x$. Observe that if $x$ is an integer, then $\lfloor x\rfloor -\lceil x\rceil$ is equal to zero; otherwise it is $-1$. As the cube root of an integer is either an integer or an irrational number, the sum in question is minus the number of numbers between $1$ and $2014$ (inclusive) which are not a cube. Since $12^3=1728<2014$ and $13^3=2197>2014$, there are exactly $12$ cubes between $1$ and $2014$, so the desired value is $-(2014-12)=-2002$.

Answer:

$2∕3$

Boris’s number is $N-2013$, so

and $N\equiv 0(\mathit{mod}2014)$. We may similarly proceed with the number $2A$:

and $2A\equiv 2\cdot 3=6(\mathit{mod}2011)$. Since $2A$ is divisible by $3$ (as it is divisible by $2013$), but neither of $2011$ and $2014$ is, we may divide the congruences for $A$ by $3$ and find that the number $2A∕3$ satisfies precisely the conditions for $N$. On the other hand, no other such $N$ is admissible, since the distance of the next closest numbers satisfying the congruences for $N$ is $2011\cdot 2014>A$. Thus $N∕A=2∕3$.

Answer:

$2^{16}-1$

Imagine the row of 16 cards as a binary number where a black side face-up corresponds to 0 and a red one to 1. A move in our game then corresponds to binary addition of some number to thus interpreted row of cards so that the sum would always remain less than $2^{16}$. Therefore the game cannot run forever and we have an upper bound for the number of moves $2^{16}-1$. This number of moves can actually be attained: consider the initial state consisting of all zeroes (i.e. all cards are black side face-up) and perform moves corresponding to adding 1 in every move.

Answer:

$\frac{27\cdot 29^2-1}{2}$

Denote the length of the second cathetus $b$ and the hypotenuse $c$. The Pythagorean theorem implies $(c-b)(c+b)=2014^{28}$. Since all the lengths are integers, the question is in how many ways we can write $2014^{28}$ as a product of two distinct, even divisors: the numbers $c-b$ and $c+b$ have the same parity, hence both must be even. The possibility $c-b=c+b$ is ruled out for it implies $b=0$. We have $2014^{28}=2^{28}\cdot 19^{28}\cdot 53^{28}$, so there are $27\cdot 29\cdot 29-1$ pairs of divisors satisfying the conditions. Given that we have to take into account also $c-b<c+b$, we get $\frac{27\cdot 29^2-1}{2}$ possible triangles.

Answer:

359

Observe that every $n\in \mathbb{N}$ can be uniquely decomposed as $n={\sum }_{k=1}^N{a}_{k}k!$ for some $N$ dependent on $n$ and $a_k\in \mathbb{N}$ such that $a_k\le k$ since $(k+1)k!=(k+1)!$. For instance $43=1+3\cdot 3!+4!$. The question asked can thus be reformulated as finding the smallest $n$ for which ${\sum }_{k=1}^N{a}_k=12$. This question can now easily be answered as the corresponding $a_k$ will be $a_1=1$, $a_2=2$, $a_3=3$, $a_4=4$ and $a_5=2$ so that $n={\sum }_{k=1}^5{a}_{k}k!=359$.

Answer:

8

Note first that for 8 participants, the average number of victories of a player is $3.5$, and hence there must be a player $v$ who won (at least) 4 times, say against players $a_1$, $a_2$, $a_3$ and $a_4$. Similarly, one of these four players must have won against at least two other of them, so without loss of generality assume that $a_1$ defeated $a_2$ and $a_3$. Finally, somebody won the match $a_2$ against $a_3$, we can without loss of generality assume it was $a_2$. Observe that the group $\{v,a_1,a_2,a_3\}$ is ordered. Hence we see $n\le 8$.

Actually $n=8$, because a smaller number of participants permits a tournament without an ordered group of 4 players. To prove this, assume without loss of generality there are 7 players $a_0,\dots ,a_6$. For every $0\le i\le 6$, consider the player $a_i$ won the match with $a_j$ where $j=(i+1)mod7$, $(i+2)mod7$, and $(i+4)mod7$. The only possible candidates for an ordered group of size 4 are quadruples of a player and the three beaten by him/her. However, such groups are not ordered.

Answer:

$2$, $8$

Given that there must be a solution, both players can be expected to behave perfectly rationally. They write sums and products of all pairs from $\{1,\dots ,9\}$. If Peter saw that the number he had been told was there only once, he would have known the original numbers immediately. But he could not infer a clear answer. Therefore Dominic might ignore all pairs of numbers that have a unique product. Then if Dominic had a unique sum, he would have known the numbers, but he did not, therefore Peter could cross out all pairs with a unique sum. And in this manner we carry on.

Answer:

$\frac{200\sqrt{3}}{9}$

Denote by $r$ the radius of the sphere and $O$ the center of the sphere. Select one of the cones and denote the center of its base as $S$, its vertex as $V$ and its tangent point with the sphere as $T$. Let $b$ be the plane in which bases of the cones lie. Let $P$ be the orthogonal projection of $O$ to $b$, $X$ be on the line $\mathit{OP}$ so that $\mathit{TX}$ is parallel with $b$, and $Y$ be the intersection of the line $VT$ and the boundary of the selected cone. Finally, denote $Z$ the orthogonal projection of $T$ to $b$.

The Pythagorean theorem implies $VY=130$. As the sphere touches the cone, $VY$ is perpendicular to $\mathit{TO}$. Hence $△\mathit{TXO}$ is similar to $△V\mathit{SY}$ and therefore $\mathit{OX}=\frac{5}{13}r$ and $\mathit{TX}=\frac{12}{13}r$. Thus $\mathit{TZ}=120-\frac{18}{13}r$. From the similarity of $△VYS$ and $△\mathit{TY}Z$, we get $YZ=(120-\frac{18}{13}r)\cdot \frac{5}{12}=50-\frac{15}{26}r$ and consequently $\mathit{SZ}=\frac{15}{26}r$. On the other hand, $\mathit{PZ}=\mathit{TX}=\frac{12}{13}r$. Observe that the base centers of the cones constitute an equilateral triangle, with the side length 100, for which $P$ is the center of mass. So $\mathit{SP}=\frac{100\sqrt{3}}{3}$ and $\mathit{SZ}=\frac{100\sqrt{3}}{3}-\frac{12}{13}r$. With two expressions for $\mathit{SZ}$, we equate $\frac{100\sqrt{3}}{3}-\frac{12}{13}r=\frac{15}{26}r$, yielding $r=\frac{200\sqrt{3}}{9}$.

Answer:

$51$

Let the columns of the hutch be called A–G and the rows 1–7. We will hold a discussion according to the position of the rabbit closest to the center. If the central cell (D4) is taken, the remaining rabbits can live only along the perimeter. By means of analysing every allowable pattern of such an accommodation and utilizing the rotational symmetry, we obtain there are 36 possibilities then.

Consider now a rabbit dwells in D3. Then we have 2 alternatives, depending on whether D6 or D7 is used. By symmetry we obtain that occupation of D3, D5, C4 or E4 yields 8 possibilities overall. If D2 is taken, we have 2 alternatives not covered by the previous case. Since one of them coincides with taking D6, we observe that occupation of D2, D6, B4 or F4 yields 6 possibilities overall. Next, if C3, B2 or C2 (or symmetries thereof) is occupied, it can be easily verified there is no way how to place the 7 remaining rabbits. Lastly, there is only one way how to place all the rabbits along the perimeter. All in all, we have $36+8+6+1=51$ possibilities.

Answer:

$\frac{9}{5}$

We will solve this problem using mass point geometry. Physical intuition states that masses on opposite sides of a fulcrum balance if and only if the products of the masses and their distances from the fulcrum are equal (in physics-speak, the net torque is zero). If a mass of weight 1 is placed at vertex $B$ and masses of weight 2 are placed at vertices $A$ and $C$, then $△\mathit{ABC}$ balances on the line $\mathit{BF}$ and also on the line $\mathit{CD}$. Thus it balances on the point $H$ where these two lines intersect. Replacing the masses at $A$ and $C$ with a single mass of weight 4 at their center of mass $F$, the triangle still balances at $H$. Thus $\frac{\mathit{BH}}{\mathit{HF}}=4$.

Next, consider $△\mathit{BDF}$. Placing masses of weight 1 at the vertices $B$ and $D$ and a mass of weight 4 at $F$, the triangle balances at $G$. A similar argument shows that $\frac{\mathit{EG}}{\mathit{GF}}=2$ and that $\frac{\mathit{DG}}{\mathit{GH}}=5$. Because $△\mathit{DEG}$ and $△\mathit{FHG}$ have congruent (vertical) angles at $G$, it follows that $\frac{[\mathit{DEG}]}{[\mathit{FHG}]}$ = $\frac{\mathit{EG}}{\mathit{FG}}\cdot \frac{\mathit{DG}}{\mathit{HG}}=2\cdot 5=10$. Thus $[\mathit{FGH}]$ = $\frac{[\mathit{DEG}]}{10}=\frac{18}{10}=\frac{9}{5}$.

Answer:

$\frac{5\sqrt{39}}{3}$

First consider a regular octahedron of side length 1, that is, the case $x=1$. To compute its volume, divide it into two square-based pyramids with edges of length 1. Such a pyramid has height $\sqrt{2}∕2$, so its volume is