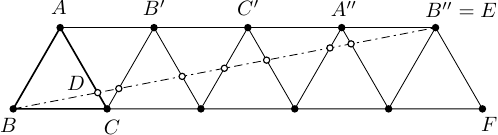
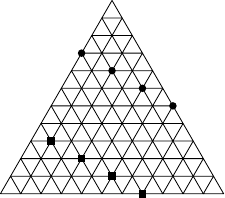
Equilateral triangle of side length is divided into small equilateral triangles of side length . We call a set of vertices of these small triangles independent if for any two distinct points the segment is not parallel to any side of . What is the largest number of elements of an independent set?Solution
Answer:
1346
Each vertex in the grid can be assigned its distances to the three sides of (taking as the unit the height of a small triangle); it is easy to see that for each vertex, these three integers add up to . On the other hand, given a triple of non-negative integers with sum , there is a unique vertex of the grid with these numbers being its distances from the sides, thus we may equivalently consider such triples instead of the vertices. We will refer to the three numbers as coordinates.
The independence condition translates to the assertion that no two triples in the set have equal the first, the second, or the third coordinate. Let
|
be an independent set. Since the numbers are distinct non-negative integers, their sum is at least
|
The same holds for the sums and . On the other hand, we have for each , and so
|
It follows that
or .
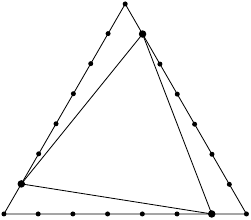
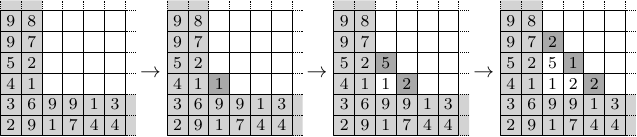
The following two sequences of points form together an independent set of size :
|
We conclude that the sought maximal number of elements is
.
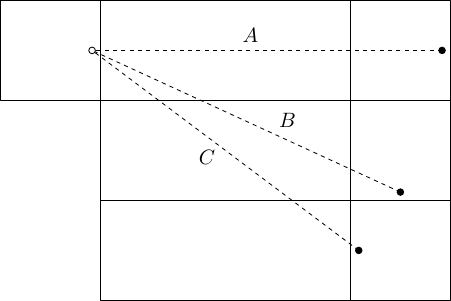
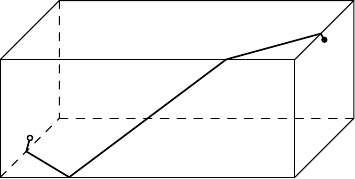
The following picture illustrates the construction of an independent set for a triangle of side length instead of :