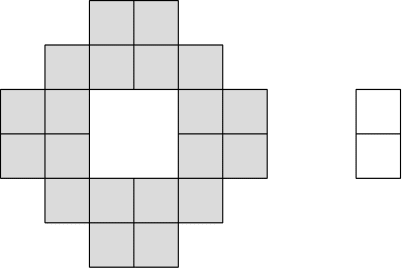
A building has floors. Each floor’s hallway is accessible via either of two main doors and provides access to four rooms. Each room has its own door, with one person living in each room. A single lock will be installed on every door, including the hallway doors, and keys will be distributed so that:
- Each person can access their own room but not anyone else’s,
- Each person can access the hallway on their floor, and
- It is allowed for someone to have access to hallways on other floors.
Each lock is associated with a unique corresponding key and can only be opened by that key. However, the same lock can be used on multiple doors if needed, and any number of copies of its corresponding key can be made and distributed. Individuals can hold as many keys as required. The company responsible for the installation aims to minimize the total cost of producing the keys. Creating a new key costs 3, and making a copy of an existing key costs 2. What is the minimal total cost of all keys while meeting the above conditions?Solution
Answer:
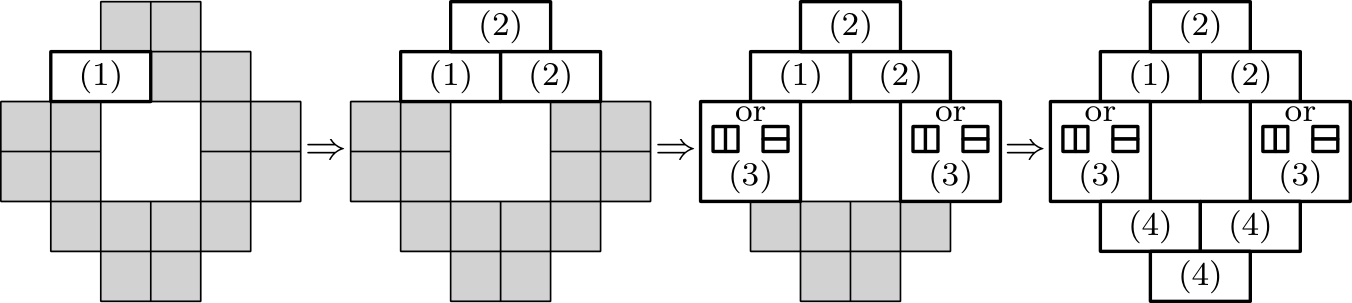
Consider a cost-optimal arrangement of locks and keys; it is clear that in such a case, no resident holds more than two keys. We further show that we may assume without loss of generality that on each floor, there is exactly one (or equivalently, at least one, as there cannot be more than one) resident who possesses only a single key. This key grants access to both their room and one of the hallway doors, while the remaining three residents of that floor use the other hallway door.
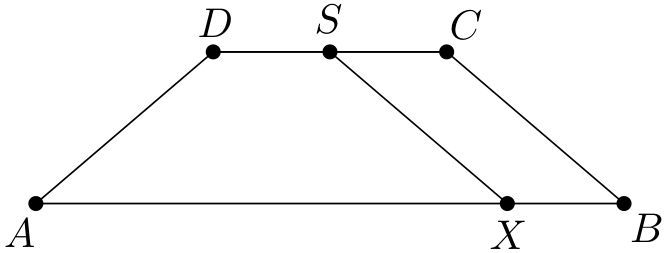
Suppose this is not the case on some floor. Then one of the hallway doors, , is used by at most two of the four residents – resident and possibly resident . If no resident among the four can unlock , we select one of them arbitrarily and treat them further as . We modify the key system as follows: replace the lock on door with a completely new one and install the same lock on ’s room door. As a result, now requires only a single key, which costs , whereas their previous two keys had a combined cost of at least . This reduces the total cost by at least .
Moreover, if resident exists, we reassign their hallway key to match the other hallway door on that floor, which does not increase the total cost. However, this way might end up with a key combination enabling access to a room on some other floor; to rectify this, we replace the lock on ’s room with a completely new one, which increases the cost by at most .
Since the total cost does not increase through this process, we conclude that the assumed configuration is at least as cost-effective as any alternative. Therefore, in what follows, we assume that there is exactly one resident with a single key on each floor.
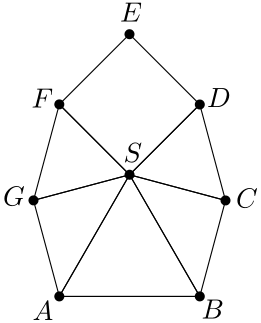
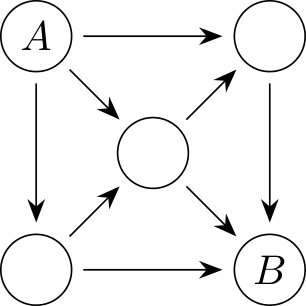
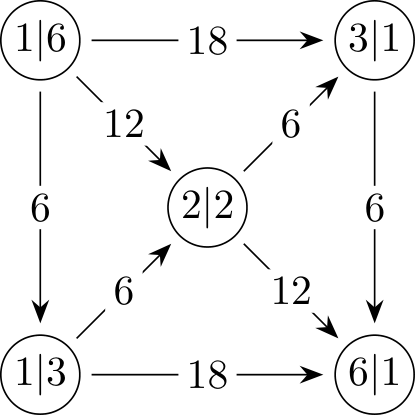
Thus, the problem reduces to minimizing the key cost for 160 floors where each hallway has only one entrance and three separate rooms. Let there be distinct key types . Each resident receives one key for their room and one key for the hallway, and these two keys cannot be of the same type. Also, no two residents can have the same pair of key types, as this would mean they have access to the same room. Therefore, the number of valid key pairs is given by .
Since we are distributing a total of key pairs, we determine the lower bound for from the inequality
Solving for a positive integer , we find that . Now, we demonstrate that it is possible to use exactly distinct key types. To achieve this, we divide the 160 floors into 32 groups of 5 floors each. The key assignments proceed as follows (the first key in the pair is for the hallway and the second for the room):
- The 15 residents in the first group receive the key pairs .
- The second group is assigned key pairs .
- This pattern continues, with the 31st group receiving key pairs .
- Finally, the last group (32nd) is assigned key pairs .
It is easy to see that this distribution satisfies the conditions given above. Therefore, is the minimal number of unique keys required, to which we add copies to cover all the keys.
Accounting for the residents possessing only a single key, a total of unique keys must be produced. Thus, the final cost is calculated as .