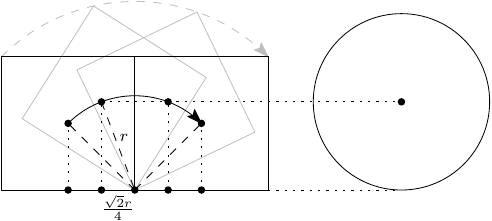
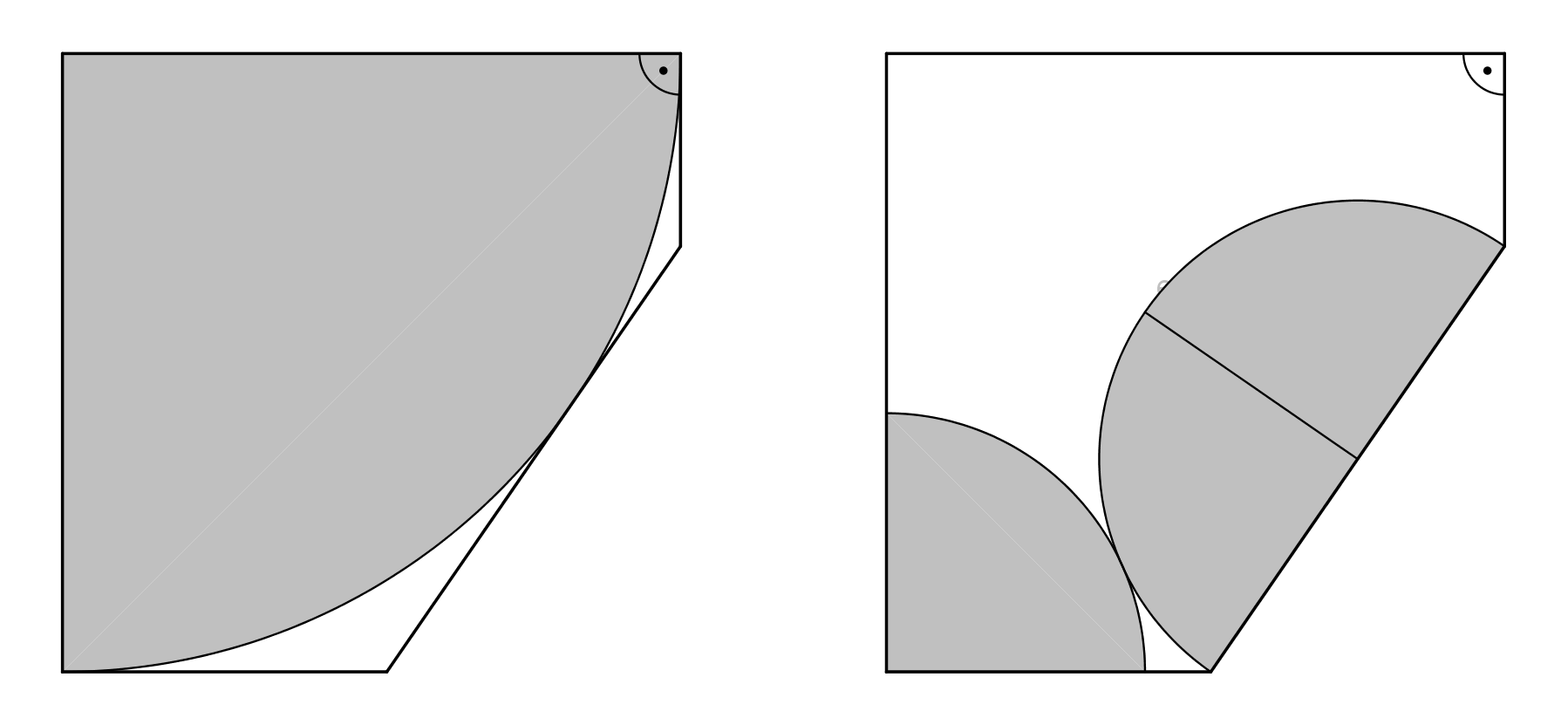
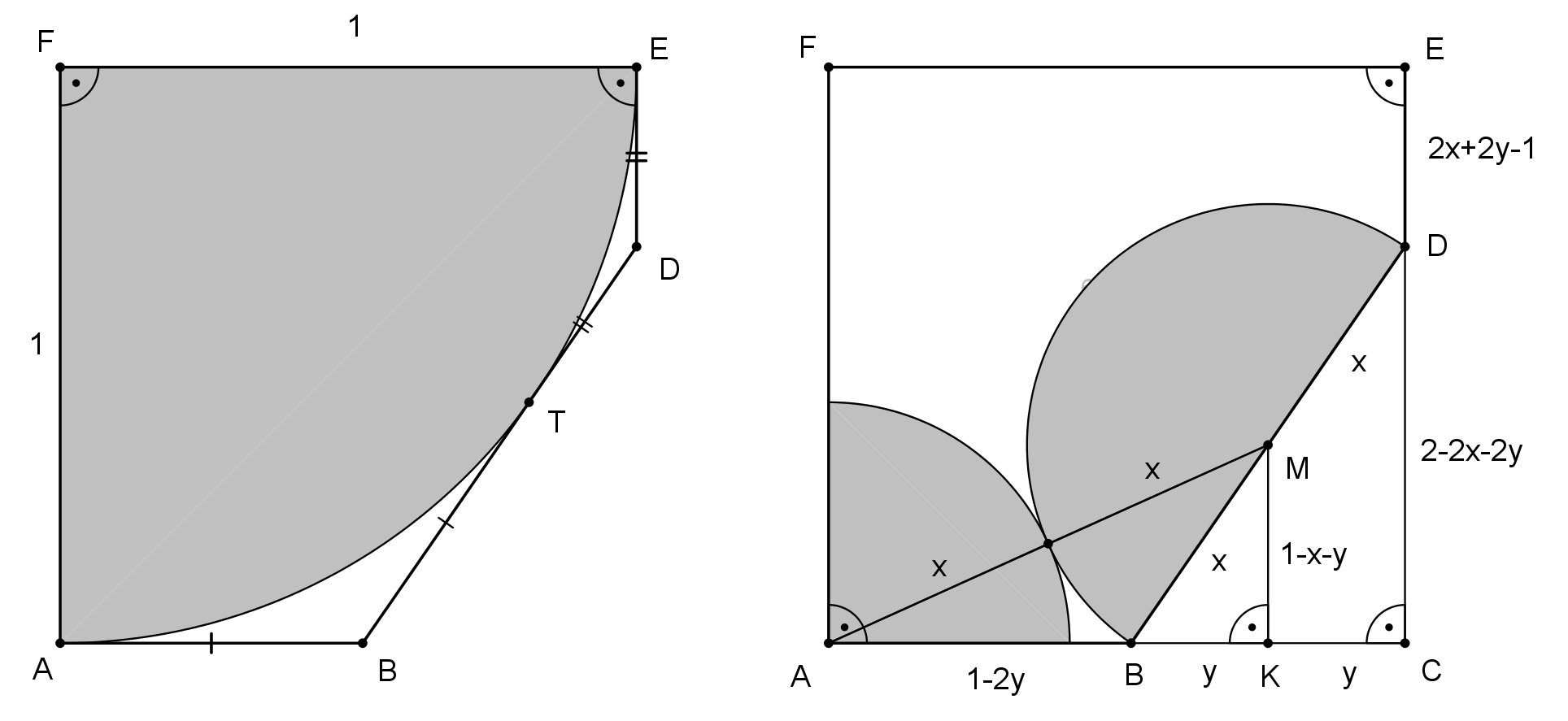
Eredmény:
, , ,
Legyenek és az első egyenlet gyökei, míg és a második egyenleté. Viète-formulák szerint
. Ezeket összevetve a következő egyenletet kapjuk:
ami pedig ilyenképp alakítható szorzattá:
Világosan látszik, hogy ha megoldás, és vagy és felcserélésével újabb megoldásokhoz jutunk. Az ilyen módon egymásba vihető megoldások közül a továbbiakban csak egyet sorolunk fel. Ha mind , mind pedig pozitív, az egyedüli megoldás. Ha valamelyik összeadandó nulla, további megoldások.
Vizsgáljuk végül azt az esetet, amikor valamely összeadandó negatív. Ez akkor fordulhat elő, ha , , és közül valamelyik . Tegyük fel, hogy . Ekkor , és az egyenlet így módosul:
Ez -höz vezet, ami csak esetén lehetséges, . Ekkor újabb megoldást ad.
Így tehát lehetséges értékei . Könnyedén leellenőrízhetjük, hogy mindegyik valóban kielégíti a feltételeket.