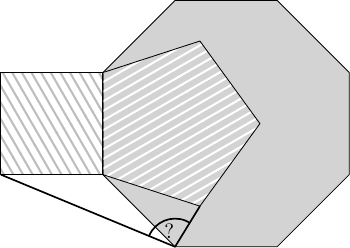
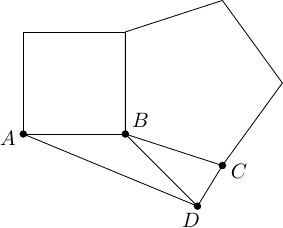
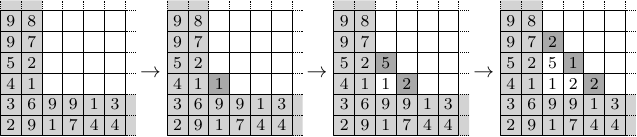
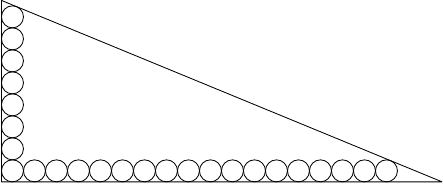
Egy szabályos háromszöget, amelynek oldalhossza , feldaraboltunk egységnyi oldalú szabályos háromszögre. A kis háromszögek csúcsainak egy halmazát függetlennek nevezzük, ha bármelyik két különböző esetén nem párhuzamos egyik oldalával sem. Legfeljebb hány eleme lehet egy független halmaznak?Megoldás
Eredmény:
1346
Minden csúcsnak a rácson megfeleltethetjük a -től vett távolságát (az egységnyi háromszög magasságában mérve). Könnyen belátható, hogy minden csúcsra ezek egész számok, amelyek összege . Másrészről, bármely nemnegatív egész számhármas, amelynek az összege , egyértelműen megad egy csúcsot a rácson. Emiatt egyértelműen megfeleltethetjük a számhármasokat és a csúcsokat. A továbbiakban a számhármas elemeit koordinátáknak hívjuk.
A függetlenségi feltétel a feladatban azt jelenti, hogy semelyik két számhármas nem egyezik sem az első, sem a második, sem a harmadik koordinátájában. Legyen
|
egy független halmaz. Mivel mind különböznek, az összegük legalább
|
Ugyanez érvényes az és összegekre. Másrészről, minden esetén, ami miatt:
|
Ebből az következik, hogy
vagy másképpen .
Az alábbi két sorozat együtt leír egy elemű független halmazt, tehát ez a méret lesz a megoldás.
|
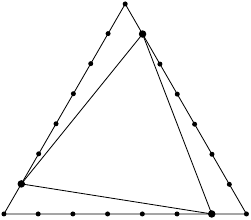
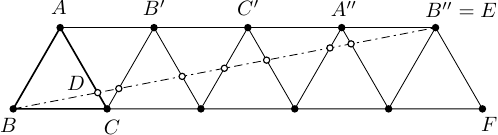
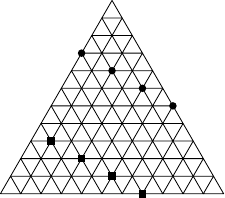
Az alábbi ábrán egy
egységnyi oldalú háromszög esetén láthatjuk az optimális független halmaz konstrukcióját.