Feladatok

Eredmény:

$58$

A megadott adatokból könnyen meghatározható, hogy a keresett életkor $21+4\cdot 4+21=58$.

Eredmény:

$56$

Az öt háromszög $S$ csúcshoz tartozó szögeinek összege $180^{\circ }$. Mivel a háromszögek egyenlő szárúak, így az öt megjelölt szög összege $\frac{5\cdot 180^{\circ }-180^{\circ }}{2}=360^{\circ }$, ebből pedig következik, hogy a kérdőjellel jelölt szög nagysága $360^{\circ }-67^{\circ }-80^{\circ }-85^{\circ }-72^{\circ }=56^{\circ }$.

Eredmény:

$32$

Adjuk össze azok számát, akikről tudjuk, hogy egy-egy versenyszámban indulnak, és ebből vonjuk ki azok számát, akikről tudjuk, hogy két versenyszámot választottak. Így a 3 lelkes versenyzőt, akik mindhárom versenyszámban indultak, már eggyel többször vontuk ki a kelleténél, így az ő számukat hozzá kell adni. Így a végeredmény: $22+13+15-8-7-6+3=32$.

Eredmény:

$90$

Összesen öt páros egyjegyű szám létezik. Ahhoz, hogy az összeg biztosan szuperpáros legyen, a hagyományos írásbeli összeadás rendszere szerint az összeadott számjegypárok összege sehol nem haladhatja meg a $10$-et. Mivel nem kezdhetünk számot $0$-val, az első számjegyre három lehetőség van ($2$, $4$ és $6$), szintén három lehetőség a második számjegyre ($0$, $2$ és $4$), a harmadik számjegyre kettő, a negyedik számjegyre egy, az utolsó számjegyre pedig öt. Ezeket a lehetőségeket összeszorozva megkapjuk az eredményt: $3\cdot 3\cdot 2\cdot 1\cdot 5=90$.

Eredmény:

$25∕4$

Tudjuk, hogy a négy kör alakú fal összkerülete lesz az új fal kerülete. Jelöljük az új kör alakú fal sugarát $r$-rel. Ekkor $2\pi \cdot 50+2\pi \cdot 100+2\pi \cdot 150+2\pi \cdot 200=2\pi \cdot r$, amiből $r=500$ adódik. Ebből a keresett arány $\frac{\pi \cdot 500^2}{\pi \cdot 200^2}=25∕4$.

Eredmény:

$9316$

Mivel a keresett négyjegyű szám osztható a $137$ és a $17$ prímszámokkal, osztható a szorzatukkal is, azaz a keresett szám $137\cdot 17=2329$ többszöröse. Mivel a kód négyjegyű, a lehetséges kódok $2329\cdot 2=4658$, $2329\cdot 3=6987$, valamint $2329\cdot 4=9316$. Ezek számjegyeinek összege rendre $16$, $23$, $30$, illetve $19$. Ezek közül csak a $23$ és a $19$ prímszám, de mivel a keresett kód a legkisebb előforduló prímszámhoz tartozik, így a lakatot a $9316$ szám nyitja.

Eredmény:

$27$

Tegyük fel, hogy az egybevágó szabályos sokszögek mind $n$ oldalúak! A szabályos sokszögek összeragasztásával kapott sokszög $3(n-3)$ oldalú, hiszen bármely két szabályos sokszögnek egy közös oldala van. Mivel egy szabályos háromszög belső szöge $60^{\circ }$, a külső $300^{\circ }$-os szöget az érintkező, a háromszög oldalaira írt egybevágó szabályos $n$-szögek felezik, tehát az $n$-szögnek $150^{\circ }$-osak a belső szögei. Mivel egy szabályos $n$-szög belső szögeinek összege $(n-2)\cdot 180^{\circ }$, így az $150n=180(n-2)$ egyenletet kell megoldanunk, amiből $n=12$ adódik. Az új alakzat oldalainak száma, és így egyúttal a keresett kerület is $3(12-3)=27$.

Eredmény:

$8081$

Az alábbiakban a szabályos háromszögeket csak háromszögeknek hívjuk. Van az eredeti háromszög, és $3\cdot 2020$ olyan háromszög, ami az eredetinek pontosan egy csúcsát tartalmazza, és végül $2020$ elforgatott háromszög amelyeknek nincs közös csúcsuk az eredetivel. Könnyű belátni, hogy ezek a háromszögek mind különbözőek, és ezeken kívül nincs más. Tehát összesen $1+3\cdot 2020+2020=8081$ megfelelő háromszög van.

Eredmény:

$\sqrt{300}\doteq 17.32051$

A szabályos nyolcszög belső szögei $135^{\circ }$-osak. Ez azt jelenti, hogy a Vera által levágott sarkak egyenlő szárú derékszögű háromszögek, melyeket összeilleszthetünk egy négyzetté, és az így kapott négyzet oldalhossza megegyezik a szabályos nyolcszög oldalhosszával. Ebből következik, hogy a nyolcszög oldalhossza $\sqrt{300}$.

Eredmény:

$853$

A második feltétel alapján tudjuk, hogy $n$-nek legalább az egyik számjegye $5$ és legalább egy számjegye páros, viszont egyik számjegye sem lehet $0$. Ebből kiindulva az első állítás az $5,2,9$ vagy $5,4,7$ vagy $5,6,5$ vagy $5,8,3$ számhármasokra teljesül. A négy lehetőség közül csak az $5,8,3$ számhármas felel meg a harmadik állításnak, így az ezekből összeállítható legnagyobb háromjegyű szám lesz a megoldás, vagyis $853$.

Eredmény:

$75928$

A tízezres helyiértéken úgy kapunk lehető legnagyobb értéket, ha a 7-estől balra álló három számjegyet töröljük. Utána már látható, hogy a maradék 2 jegy, amit törölni érdemes, a 0 és az 1. Tehát a megmaradó szám $75928$.

Eredmény:

$12$

A $2021$ akkor és csak akkor szerepel az $S_n$ számsorozatban, ha $2021=1+\mathit{an}$ valamilyen pozitív egész $a$-ra. Tehát $2020=\mathit{an}$, azaz $n$ osztója 2020-nak. A prímfelbontása $2020=2^2\cdot 5\cdot 101$. Egy osztót úgy kapunk, hogy valahány prímtényezőt felhasználunk. A $2$-es prímtényezőt bevehetjük 2-szer, 1-szer vagy 0 szor, az 5-öt és a 101-et vagy bevesszük, vagy nem. Ez összesen $3\cdot 2\cdot 2=12$ lehetőség, azaz $2020$-nak 12 osztója van. Ezek alapján 12 darab olyan $n$ van, amelyre 2021 tagja az $S_n$ sorozatnak.

Eredmény:

$510$

Bármelyik $A$ robot esetében meg tudjuk állapítani, hogy $A$ melyik másik robottal fog legutoljára találkozni és kiszámolhatjuk, hogy ez a találkozás mikor fog bekövetkezni. A leghosszabb kiszámolt idő $8,5$ perc, ami egyenlő $510$ másodperccel, így ez utóbbi értéket keressük.

Eredmény:

$42$

Az $\mathit{APD}$ és $\mathit{BCP}$ háromszöge együtt a paralelogramma területének felét fedik le. Ez alapján az $\mathit{ABP}$ háromszög területe

Eredmény:

$107$

A különbségeket nézve $1486-1058=428$ és $2021-1486=535$. Mivel a számok ugyanazt a maradékot adták $d$-vel osztva, a különbségeik $d$ többszörösei. $428$ and $535$ legnagyobb közös osztója $107$, ami prímszám, ezért a keresett szám $107$.

Eredmény:

$3024$

Ha egymás mellé sorbaállítanánk a tíz cserejátékost, összesen kilenc rés lenne közöttük. Ezen rések mindegyikébe legfeljebb egy csapatvezető kerülhet. Mivel négy vezető van, összesen $9\cdot 8\cdot 7\cdot 6=3024$ különböző módon ülhetnek le, hogy teljesüljön a feltétel.

Eredmény:

$\sqrt{3}∕6\doteq 0.288675$

A gúla alapjának $1$ egység hosszúak az élei. Ha a gúla teljes felszíne $3$, akkor a négy háromszög alakú oldalának egyenkénti felszíne $1∕2$ és így ezek magassága $1$. Tehát ha a gúlát csúcsában és két oldalának magasságvonalában kettévágjuk, akkor egy $1$ oldalhosszúságú egyenlő oldalú háromszöget kapunk, melynek magassága a gúla magasságával egyenlő. Ezért a gúla magassága $\frac{1}{2}\sqrt{3}$. Mivel a gúla térfogata egyenlő az alap és a magasság szorzatának egyharmadával, a végeredmény $\frac{1}{3}\cdot 1\cdot \frac{1}{2}\sqrt{3}=\frac{1}{6}\sqrt{3}$.

Eredmény:

$2250$

Legyen $x$ literben a bor mennyisége, $z$ pedig a vízé, még a Kána gépbe öntés előtt. Tudjuk, hogy a gép $0,06z$ liter vizet változtat borrá és $0,1x$ liter bort vízzé, valamint hogy $x$ értéke ugyanannyi a gép működése előtt és után, emiatt igaz, hogy $0,06z=0,1x$. Illetve, mivel $x+z=6000$, felírhatjuk, hogy $0,06(6000-x)=0,1x$. Az egyenletet $x$-re megoldva $6000\cdot \frac{3}{8}=2250$-et kapunk.

Eredmény:

$35$

Könnyen beláthatjuk, hogy az egyenlő oldalú háromszög beírt köre feleakkora, mint a köréírt köre, így az ábrán látható beírt kör területe $\frac{140}{4}=35$. Továbbá a szürkére színezett rész pontosan $\frac{1}{3}$ része a két kör közötti különbségnek, vagyis ugyancsak $35$.

Eredmény:

$4044$

Jelöljük az egész számokat a következőképp: $c_1\ge c_2\ge \cdots \ge c_{2020}\ge c_{2021}\ge 1$. Arra vagyunk kíváncsiak, hogy mekkora $c_1$ lehető legnagyobb értéke, ha a

egyenlet teljesül. Osszunk az egyenlet bal oldalával, és becsüljük meg felülről a kifejezést úgy, hogy $c_3$-tól kezdve a nevezőkben lévő kisebb $c_i$ számok értékét $1$-nek rögzítjük:

Ha szorzunk $c_1{c}_2$-vel és átrendezzük az egyenletet, megkapjuk, hogy

Ha $c_2\ge 3$, akkor $c_1\le 4044$, és szélsőséges esetben a $c_1=4044$, $c_2=3$, $c_3=\cdots =c_{2021}=1$ számhármas teljesíti is az (1)-es egyenletet – ennél nagyobb $c_1$ értéket ebben az esetben nem kaphatunk. Ugyanakkor ha $c_2\le 2$, akkor a $c_2\ge c_3\cdots \ge c_{2021}$ számok közt $k\ge 0$ kettes és $2020-k$ egyes található, így az (1)-es egyenletet átírhatjuk a következőképp:

Ezt tovább egyszerűsíthetjük $c_1(2^{k-1}-1)=2020+k$ alakra és így beláthatjuk, hogy $k\le 1$-re nincs olyan $c_1$, amire teljesül ez az egyenlet, $k\ge 2$-re pedig megkapjuk, hogy

így a végeredmény $4044$.

Eredmény:

$59$

Először figyeljük meg, hogy három mezőnek van egy szomszédja, másik háromnak kettő, és még másik háromnak három. Ez azt jelenti, hogy ha egy $p$ prím a kilenc szám egyike, akkor $p$-nek legalább egy többszörösének is a számok közt kell lennie. Továbbá vegyük észre, hogy az $1$ nem lehet a számok egyike. Jelöljük egy lehetséges kitöltés kilenc számának összegét $S$-sel.

Ha egy lehetséges kitöltésben szerepel egy $p\ge 11$ prím, akkor legalább egy $k\cdot p$ többszörösnek szintén szerepelnie kell, ahol $k\ge 2$. Töltsük ki a fennmaradó hét kis háromszöget a lehető legkisebb számokkal, nem figyelve arra, hogy teljesüljön rájuk a közös osztós szabály.

Ekkor $S\ge 2+3+4+5+6+7+8+p+k\cdot p=35+(k+1)\cdot p\ge 35+33=68$.

Most tegyük fel azt, hogy nincs $p\ge 11$ prím egy lehetséges kitöltésben, és nézzük meg a következő négy alesetet:

• Az $5$ és a $7$ egyaránt szerepel: $S\ge 5+k_5\cdot 5+7+k_7\cdot 7+2+3+4+6+8=(k_5+1)\cdot 5+(k_7+1)\cdot 7+23\ge 15+21+23=59$
• Az $5$ szerepel, de a $7$ nem: $S\ge 5+k\cdot 5+2+3+4+6+8+9+\{\begin{array}{c}10\ge 20+32+10=62\text{ha}k\ge 3\hfill \\ 12=15+32+12=59\text{ha}k=2\hfill \end{array}$
• Nem szerepel sem az $5$, sem a $7$: $S\ge 2+3+4+6+8+9+10+12+14=68$
• A $7$ szerepel, de az $5$ nem: $S\ge 2+3+4+6+7+8+9+10+k\cdot 7\ge 49+14=63$

Összességében arra juthatunk, hogy az $59$ esélyes a legkisebb összeg értékére, amennyiben kitöltéskor teljesül a közös osztós feltétel. A fenti esetek közül mindkét $59$ összegű számcsoportot be tudjuk írni a háromszögbe a szabályok betartásával:

Tehát a válasz $59$.

Eredmény:

$93$

Legyen egy ház területe 3 egység.

Az első házban összeszámolhatunk nyolc háromszöget, melyek mérete 1/4, nyolcat, melyek mérete 1/2 és hármat, melyek mérete 1. Ez összesen 19 háromszög.

A második házban ugyanennyi háromszög található, plusz két 1 egység méretű háromszög, melyek ebből a házból átlógnak az előző ház területére. Tehát a második házban 21 háromszöget számolunk össze.

A harmedik háztól számítva mindegyik újonnan lerajzolt ház ugyanannyit ad hozzá a háromszögek számához, mint a második ház, plusz egy 4 egység méretű háromszöget, ami átlóg az előző két ház területére. Vagyis a harmadiktól számítva mindegyik későbbi ház 22 háromszöget tartalmaz.

Mivel $2021-19-21=1981$ és $1981=90\cdot 22+1$, Lilinek legalább $2+90+1=93$ házat kell lerajzolnia.

Eredmény:

$\frac{15}{4}$

A $\mathit{BEG}$ és $\mathit{BEF}$ háromszögek területének aránya $4:3$. Mivel ennek a két háromszögnek közös a $\mathit{BE}$ oldala, az erre az oldalra mért magasságuk aránya is $4:3$. Az $\mathit{ABG}$ és $\mathit{CDF}$ háromszögeknek ugyanakkora a területe, így megkapjuk, hogy $\mathit{AB}=\frac{3}{4}\mathit{CD}=\frac{15}{4}$.

Eredmény:

$6375$

Anna egészen addig tud páratlan szélességű csíkokat levágni, amíg $1+3+\cdots +2n-1=n^2<2100$. Mivel $45^2=2025<2100<2116=46^2$, a $89$ szélességű a legutolsó páratlan szélességű csík, amit levághat. Továbbá addig tud páros szélességű csíkokat levágni, amíg $2+4+\cdots +2n=n(n+1)<2155$. Tekintve, hogy $45\cdot 46=2070<2155<2162=46\cdot 47$, a legnagyobb páros szélességű csík, amit Anna levághat, $90$ széles. Így a megmaradt téglalap területe $(2100-2025)\cdot (2155-2070)=75\cdot 85=6375$.

Eredmény:

$\frac{10}{3}$

Legyen $w$ a keresett gyűrűszélesség és figyeljük meg a két egymáson lévő gyűrű felülnézeti képét:

Ebből következik, hogy az asztal fölött függőlegesen álló gyűrű magassága $1=w-x$. Így $8=2x+w=2(w-1)+w=3w-2$ és ebből megkapjuk, hogy $w=\frac{10}{3}$.

Eredmény:

$29030400$

A polinomot felírhatjuk $c\cdot (x-a_1)\cdot (x-a_2)\cdot \cdots \cdot (x-a_{14})$ alakban, ahol $a_1,a_2,\dots ,a_{14}$ páronként különböző egészek és $c$ egy pozitív szám (mivel $c$ maga a főegyüttható). A $0$-nál felvett érték megegyezik a $c\cdot a_1\cdot a_2\cdot \cdots \cdot a_{14}$ szorzattal. Mivel ennek a minimum értékét keressük, $c$-nek a lehető legkisebb értéket adjuk, tehát $c=1$. Hogy minimalizáljuk a többi gyök összegét, a nullához lehető legközelebbi értékeket kell nekik adnunk, vagyis $1,-1,2,-2\dots$. Azonban páros darab negatív számot kell kiválasztanunk, így a végeredmény $6!\cdot 8!=29030400$.

Eredmény:

$8783$

Ha Bea leírja az egész számokat $1$-től $2021$-ig, akkor $9$ egyjegyű számot, $90$ kétjegyű számot, $900$ háromjegyű számot és $2021-1000+1=1022$ négyjegyű számot ír le. Összesen $9+90\cdot 2+900\cdot 3+1022\cdot 4=6977$ számjegyet ír le. Az összes számjegyhez szükséges egy tollvonás, továbbá még egy tollvonást igényel a $4$, $5$ vagy $7$ értékű számjegyek leírása. Tehát elég összeszámolnunk, hogy hányszor fordulnak elő ezek a számjegyek. Mivel a $2021$ nem tartalmazza a $4$, $5$ és $7$ számok egyikét sem, csak a $2020$-nál nem nagyobb egész számokat nézzük.

Számoljuk meg a Bea által leírt $4$-es számokat. A $2020$-ig leírt számok $1∕10$ része tartalmazza a $4$-et az egyes helyiértéken, vagyis $202$ szám. A tízes helyiértéken a $2000$-ig leírt számok $1∕10$ részében fordul elő a $4$, $2001$ és $2020$ között egyszer sem. Ez összesen $200$ előfordulás a tízesek helyén. Hasonlóképp a százas helyiértéken $200$-szor szerepel a $4$. Bea összességében $202+200+200=602$-szer írja le a $4$-es számjegyet. Ugyanez a helyzet az $5$-tel és a $7$-tel is.

Következésképp Bea $6977$ számjegyet ír le, melyek közül $3\cdot 602=1806$ a $4$, $5$ és $7$ számok egyike. Tehát összesen $6977+1806=8783$ tollvonást használ.

Eredmény:

$3845$

A jelölés könnyebbsége érdekében a megadott táblázatot egy tizenhat elemből álló $f$ sorozatnak tekintjük. A három megadott elem, vagyis $f(6)=6,f(7)=7,f(9)=2$ alapján egyenként megkapjuk, hogy $f(13)=6$, $f(15)=7$ és $f(12)=2$.

Alapvetően két megoldási módszer létezik: vagy azt nézzük meg, hogy egy adott számpár hova kerülhet, vagy azt, hogy egy adott cellába melyik számok kerülhetnek (a Sudokuhoz hasonlóan).

Példaképp nézzük meg, hogy a két $3$-as számot hogy írhatjuk be a táblázatba. Három lehetőség létezik: $f(1)=f(5)=3$ vagy $f(4)=f(8)=3$ vagy $f(10)=f(14)=3$.

Beláthatjuk, hogy az $f(10)=f(14)=3$ megoldás esetén egyedül $f(16)=4$ kerülhet az $f(16)$-os cellába és emiatt $f(11)=4$. Viszont így már sehogy sem tudnánk beírni a két $8$-ast a táblázatba. Az $f(4)=f(8)=3$ megoldás két lehetőséget ad az $5$-ös számpár elhelyezésére: $f(5)=f(11)=5$ vagy $f(10)=f(16)=5$. Mindkét lehetőség azonnali ellentmondást eredményez.

Az $f(1)=f(5)=3$ megoldás egyetlen lehetőséget hagy az $f(2)=f(11)=8$ elhelyezésére, így a maradék cellákat csak egyféleképp tudjuk kitölteni a szabálynak megfelelően: $f(4)=f(10)=5$, $f(3)=f(8)=4$ és $f(14)=f(16)=1$.

Tehát az egyetlen megoldásból származó négyjegyű megoldás a $3845$.

Eredmény:

$5.7=\frac{57}{10}$

Mivel $50^{\circ }+65^{\circ }+65^{\circ }=180^{\circ }$ és van két-két egymással párhuzamos szakasz, a feladatban lévő hatszöget megkapjuk, ha az $A{E}^{\prime }{D}^{\prime }F$ paralelogrammát összehajtjuk a $\mathit{BC}$ szakasz mentén (mivel $\mathit{BAF}\sphericalangle =\mathit{CDE}\sphericalangle$, így valóban paralelogramma; lásd az ábrát). Ezzel megegyező eredményt kapunk, ha a $D$ és $E$ csúcsokat a $\mathit{BC}$ szakasz egyenesére tükrözzük. Ha ezek mellett megfigyeljük, hogy $\mathit{BCG}$ egyenlő szárú háromszög, az oldalhossz-feltételekből következik, hogy $\mathit{CD}=\mathit{AB}+B{E}^{\prime }-\mathit{CF}=\mathit{AB}+\mathit{EG}-\mathit{FG}=5.7$.

Eredmény:

$36$

Nézzünk meg egy $4\times 2$-es táblarészt. Ahogy az első két ábrán látszik, egy mező megjelölése még nem jelent biztos találatot, mivel még egy módon el lehet helyezni a cirkálót, hogy ne érje találat. Továbbá egyértelmű, hogy ha egy mezőt választunk az egyik sorban és egyet a másikban, akkor lehetetlen elrejteni a cirkálót ezen a táblarészen; a harmadik ábra ezt szemlélteti. Tehát minden $4\times 2$-es táblarészen szükség van legalább két lövésre, vagyis összesen legalább $18\cdot 2=36$-ot kell lőnie Sárának.

Alternatív megoldásként az alábbi átlós lövésmintázat a $12\times 12$-es játéktáblán szintén jó szemlélteti, hogy $36$ lövés elégséges ahhoz, hogy Sára legalább egyszer eltalálja a cirkálót.

Eredmény:

$13$

Mivel $\mathit{ABC}$ hegyesszögű, beláthatjuk, hogy a $T=\frac{1}{2}a{h}_a$ terület maximalizálásához a $h_b$ és $h_c$ magasságoknak a lehető leghosszabbnak kell lenniük. Így $h_b=h_c=a-1$, ezáltal $\mathit{ABC}$ egyenlő szárú. Nevezzük a $\mathit{BC}$ oldal felezőpontját $M$-nek és a $h_c$ magasságvonal talppontját $C_0$-nak. Ha a Pitagorasz-tételt alkalmazzuk az $\mathit{ABM}\sim \mathit{CB}{C}_0$ hasonló derékszögű háromszögekre, megkapjuk, hogy

Mivel $101,4$ racionális szám, $2a-1$-nek mindenképp páratlan négyzetszámnak kell lennie, ${(2k+1)}^2$ alakban, ahol $k\ge 0$ egész szám, és így $a=\frac{{(2k+1)}^2+1}{2}\in \{1,5,13,25,41,\dots \}$. Az első néhány értéket behelyettesítve észrevehetjük, hogy a terület szigorúan növekszik $a$ növelésével, és megtalálhatjuk, hogy a helyes megoldás $a=13$.

Eredmény:

$3099$

Jelöljük $n_1=101,n_2,\dots ,n_{1000}$-rel ezt a pozitív egsézekból álló sorozatot. Feltéve, hogy két szomszédos szám közötti különbség mindig 2, azt kapjuk, hogy $n_{1000}=101+2\cdot 999=2099$ és ${\sum }_{i=1}^{1000}{n}_i=2200\cdot 500=1100000$. Tehát a Ludwig által kapott összeg és a lehető legkisebb összeg közötti különbség $100500=20100\cdot 5$. Ha $n_{i+1}-n_i=7$, kettő helyett, akkor az összeg $(1000-i)\cdot 5$-tel nő, $n_{1000}$ pedig öttel nő. Ezért ahhoz, hogy maximalizáljuk $n_{1000}$-t, de az összeg továbbra is $1200500$ legyen, a 7-es távolságokat a lehető legnagyobb sorszámú tagok között kell elhelyeznünk. Tehát Ludwig hétre állítja a távolságot $n_{i+1}-n_i$ között, ahol $i=800,\dots ,999$ (az összes többi helyen a távolság továbbra is 2) és így megkapja $n_{1000}$ lehető legnagyobb értékét: $n_{1000}=101+2\cdot 999+200\cdot 5=3099$.

Eredmény:

$29292929292$

Vegyük észre, hogy $100\equiv 1$ (mod $11$). Emiatt egy számot 100-zal szorozva nem változik meg a 11-es maradéka. Ha egy szám tartalmaz két egymást követő azonos $a$ számjegyet, akkor felírható $x\cdot 10^{n+2}+11a\cdot 10^n+y$ alakban, amiből kitörölve ezt a két számjegyet $x\cdot 10^n+y$-t kapunk, amelynek ugyanaz a 11-es maradéka, mint az eredeti számnak.

Tehát a keresett válaszban nem szerepel két egymást követő kettes vagy kilences, különben törölnénk őket és kisebb számot kapnánk. Szóval próbáljuk ki a $2929\cdots 292$ vagy $9292\cdots 929$ alakú számokat, amíg el nem érünk egy 11-gyel oszthatót.

Segít a válaszban, ha ismerjük a 11-gyel való oszhatóság kritériumát. Egy szám akkor és csak akkor osztható 11-gyel, ha a páros helyiértéken álló számjegyek összegéből kivonva a páratlan helyiértéken álló számjegyek összegét, 11-gyel osztható számot kapunk. Mivel felváltva használjuk a 2-eseket és 9-eseket, keressük a legkisebb $n$-t amelyre $2n-9(n+1)$ vagy $9n-2(n+1)$ 11 többszöröse. Mindkét esetben $n=5$ megfelelő, tehát $29292929292$ és $92929292929$ jó jelöltek. A kettő közül a kisebb számot választjuk.

Eredmény:

$(3+\sqrt{5})∕2\doteq 2.61803$

Vegyük észre, hogy a $p$ és $q$ ötszögek párhuzamosan hasonlóak az $F$ pontra tükrözve (és nagyítva), így az $X$ és $Z$ pontok közti szakasz áthalad az $F$ ponton. Ez a szakasz az egyik lehetőség a kettőből, ha a $p$ és $q$ ötszögek egy-egy csúcsa közti legnagyobb távolságot keressük.

Az egyes csúcsokban lévő szögek értékét végigkövetve a következőkre juthatunk: (1) $\mathit{AFE}\sphericalangle =108^{\circ }$, így a koszinusztörvény miatt $\mathit{AE}=\frac{1}{2}(1+\sqrt{5})$; (2) az $\mathit{AFZ}$, $\mathit{XFD}$, $\mathit{DFE}$ háromszögek egyenlő szárúak. Tehát

és

Vagyis a keresett távolság $\mathit{XF}+\mathit{ZF}=\frac{1}{2}(3+\sqrt{5})$.

Eredmény:

$281$

Az egyenletet át tudjuk alakítani erre: $a(\mathit{bc}-11b-175)=\mathit{bc}$. Ebből következik, hogy $a=b$ vagy $a=c$, mivel ezek prímek. Az első esetben $\mathit{ac}-11a-175=c\iff (a-1)(c-11)=186$, amiből a $(2,2,197)$ az egyenlet megoldása a prímek körében. A másik esetben $\mathit{ab}-11b-175=b\iff 175=b(a-12)$, amiből az alábbi két megoldást kapjuk a prímek körében: $(47,5,47)$ és $(37,7,37)$. Vagyis a lehetséges $c$ értékek összege: $197+47+37=281$.

Eredmény:

$\frac{21}{40}$

Mária bármely sorrendje esetén az kell nekünk, hogy Tamásnak a 3 legjobb háza közül pontosan egy legyen Mária 3 legjobb háza közt, a másik kettő pedig Mária sorrendjében a 4. és a 10. közt. Mária bármely sorrendje esetén, Tamás esélye

Eredmény:

$-2$

A $p(x)$ polinomot az alábbi szorzattá tudjuk bontani $(\mathit{ax}+b)(x^{2020}+x^{2019}+\cdots +x^2+1)$, ahol a második tag pozitív, így az $x=\frac{-b}{a}$ lesz a $p(x)$ polinom egyetlen valós gyöke.

Mivel a $q(x)$ polinomnak egy gyöke van, ezért a diszkrimináns $b^2-4a^2=0$, és mivel $a,b$ pozitív, ezért $b=2a$. Vagyis $x=\frac{-b}{a}=\frac{-2a}{a}=-2$.

Eredmény:

$312$

Feltételezhetjük, hogy $n<p$ és hogy az $\frac{n}{p}$ tizedestört alakja $5$ jegyenként ismétlődik rögtön a tizedesjegy után. (Ha $\frac{n}{p}$ csak később lesz ismétlődő, akkor elcsúsztathatjuk a tizedesjegyet úgy, hogy $n$-t megszorozzuk $10$ megfelelő hatványával, majd, ha így $n\ge p$, akkor lecseréljük $n^{\prime }<p$-re, ahol $n=\mathit{kp}+n^{\prime }$: ez mindössze "kitörli" a szám egészrészét.) Ha az $\frac{n}{p}$ ismétlődő tizedestört alakja $0.\overline{\mathit{ABCDE}}$, akkor $99999\cdot \frac{n}{p}=10^5\cdot \frac{n}{p}-\frac{n}{p}=\mathit{ABCDE}$ egész szám. Mivel $n<p$ és $p$ prímszám, következik, hogy $p\mid 99999$, vagyis $p\mid 3^2\cdot 41\cdot 271$. Mind $1∕3$-nak, mind $2∕3$-nak egyjegyű az ismétlődési ciklusa, viszont $1∕41=0.\overline{02439}$ és $1∕271=0.\overline{00369}$ megfelelnek a kitételnek, így a végeredmény $41+271=312$.

Eredmény:

$5680$

$10=\left(\genfrac{}{}{0.0pt}{}{5}{3}\right)$ olyan kimenet létezik, ahol mindannyian ugyanazt a három nyelvet beszélik. Ahhoz, hogy legalább két közös nyelvük legyen, $10=\left(\genfrac{}{}{0.0pt}{}{5}{2}\right)$-féleképp választhatjuk ki ezt a két nyelvet, majd $3^4$ módon választhatjuk ki a négy ember harmadik nyelvét. Ha azt akarjuk, hogy legalább egy közös nyelvük legyen, $5=\left(\genfrac{}{}{0.0pt}{}{5}{1}\right)$-féleképp választhatjuk ki az egy közös nyelvet, majd ${\left(\genfrac{}{}{0.0pt}{}{4}{2}\right)}^4=6^4$ módon választhatjuk ki a négy ember két-két másik nyelvét. A szitaformulát alkalmazva megkapjuk a keresett eredményt, ami $5\cdot 6^4-10\cdot 3^4+10=6480-810+10=5680$.

Eredmény:

$\frac{65}{98}$

Olyan törtszámokkal kell próbálkoznunk, amelyeknek a lehető legnagyobb a nevezője, mert ha $\frac{a}{b}$ kisebb, mint $\frac{2}{3}$, akkor $\frac{a+2}{b+3}$ nagyobb, mint $\frac{a}{b}$, viszont kisebb, mint $\frac{2}{3}$. Ez azt jelenti, hogy a 98, 99 és 100 nevezőkkel érdemes próbálkozni. A lehetséges megoldások tehát $\frac{65}{98}$, $\frac{65}{99}$ és $\frac{66}{100}=\frac{33}{50}$. Ha összehasonlítjuk ezeket a törteket, megkapjuk, hogy

Eredmény:

$130$

A fekete alakzat felszíne megyezik a fekete kockák felszínével mínusz kétszer azok a lapok, ami két fekete kockának a határa. Ezek a párok háromféleképpen állhatnak: "fel-le", "elöl-hátul" és "balra-jobbra". A "balra-jobbra" párok esetén, a két fekete kocka elölről és felülről nézve is egy-egy vízszintesen érintkező oldalpárt alkot, melyek azonos oszlopokban szerepelnek a két vetület esetén. Végignézve az oszlopokat láthatjuk, hogy ilyen nem fordul elő. Az "elöl-hátul" érintkezéshez a bal oldali négyzetben kell két négyzetnek függőlegesen érintkeznie. Ez kétszer fordul elő az első oszlopban. Mivel a jobb oldali ábrán az első oszlopban csak egyetlen fekete négyzet van, így tudjuk, hogy ez a két érintkezés a nagy kockában is két érintkezés lesz. A "fel-le" párok esetén az előzőhöz hasonló esetet kapunk, csak a két ábrát felcserélve kell nézni (ekkor az ötödik oszlopban lesz két érintkezés, amik valóban érintkezés lesz, mivel a felülről nézve csak egy kocka szerepel az ötödik oszlopban). Összesítve a kérdéses felszín mérete $6\cdot 23-2\cdot 4=130$.

Eredmény:

$204$

Tudjuk, hogy $720=2^4\cdot 3^2\cdot 5$. A $d_1,d_2,\dots d_k$ sorozatban bármely $p$ prím kitevői monoton növekvő sorozatot alkotnak, melyek összege $p$ kitevője $720$ prímtényezős alakjában. Ez a sorozat $p=2$ esetében lehet $(1,1,1,1)$, $(1,1,2)$, $(2,2)$, $(1,3)$, $(4)$, vagy ezek közül bármelyik tetszőleges számú nullával az elején. $3$ esetében lehetséges véggződése a sorozatnak $(1,1)$ vagy $(2)$, $5$ esetében pedig csak az $(1)$. Ezen sorozatok bármelyik kombinációjával osztó felbontást kapunk. Vagyis $720$-nak összesen $10$ osztó felbontása létezik és ezek vezetőinek számtani közepe $\frac{2+4+4+8+16}{5}\cdot \frac{3+9}{2}\cdot 5=204$.

Eredmény:

$9450$

Legyen a $N$, $A$, $B$, $O$, $J$ betűkkel ellátott játékkockák száma egyenként $n$, $a$, $b$, $o$, $j$. Azoknak a $(n,a,b,o,j)$ ötös számcsoportoknak a számát keressük, amelyekre igaz, hogy

Mindegyik prímtényezőt szétoszthatjuk a $n$, $a$, $b$, $o$, $j$ számok közt és különféle felosztások különféle ötös számcsoportokat eredményeznek. Összesen

módon tudjuk szétosztani a $2$-eseket, ami rendre a prímtényező $5$-ös kitevőjének az alábbi felosztásaival egyezik meg: $5$, $4+1$, $3+2$, $3+1+1$, $2+2+1$, $2+1+1+1$, $1+1+1+1+1$. Továbbá

módon tudjuk szétosztani a $3$-asokat, ami a kitevő $2$ és $1+1$ felosztásaival egyezik meg. Végül pedig

módon oszthatjuk ki az $5$-ös prímtényezőt. Ez összességében

különböző Scrabboj játékcsomag.

Eredmény:

$4978$

Beláthatjuk, hogy az összeadás mindhárom tagja tökéletes négyzet, hiszen $4=2^2$. Így ha kiválasztunk közülük kettőt és négyzetre emeljük az összegüket, akkor megkaphatjuk pl. a következőt:

Ha ezt a kifejezést megfeleltetjük a feladatban szereplő egyenlettel, akkor arra jutunk, hogy

és erre az értékre mindenképp tökéletes négyzetet kapunk. A három tag közül még kétféleképp lehet kettőt kiválasztani, ha ezeken elvégezzük ugyanezeket a lépéseket, akkor $n=541$-et és $n=2761$-et kapunk. Így feltételezhetjük, hogy az $n=4978$ a keresett megoldás. Ennek bebizonyításához mutassuk meg, hogy $4^{2021}+4^n+4^{3500}$ nem tökéletes négyzet, ha $n=4978+m$, ahol $m$ pozitív egész szám. A

kifejezés akkor és csak akkor tökéletes négyzet, ha $(1+4^{1479}+4^{2957+m})$ is tökéletes négyzet, mivel $4^{2021}={\left(2^{2021}\right)}^2$. Viszont a

kifejezésből látszik, hogy a második tényező biztosan két egymást követő négyzetszám között van. Ezért $n=4978$ a keresett megoldás.

Eredmény:

$1021616$

Vegyük a

polinomot és lássuk be, hogy minden nem nullával egyenlő együtthatója pozitív. Azt állítjuk, hogy ezek az együtthatók pontosan megegyeznek az $x^k$ kitevőivel, ahol $k$ értéke a lehető legkisebbtől, vagyis $0$-tól, a legnagyobbig, vagyis $S:=2+\cdots +2021=2043230$-ig terjed, kivéve pontosan két értéket: $1$ és $S-1$. Ha elképzeljük a $Q$-t definiáló $2020$ tag szorzatát, világos, hogy nincs benne lineáris tag, és ugyanez mondható el az $x^{S-1}$-ről is: ha mindegyik zárójelből kiválasztjuk az $x$-ek kitevőjét, megkapjuk $x^S$-t, máskülönben a kitevő legfeljebb $S-2$.

Most azt kell bebizonyítanunk, hogy a fenti tartományban az összes többi kitevő pozitív együtthatóval van jelen, vagy ezzel ekvivalensen azt, hogy a legkisebb $1$-nél nagyobb szám, ami nem felírható a $\left\{2,3,\dots ,2021\right\}$ egy részhalmazának összegeként (nevezzük ezt a számot $m$-nek) egyenlő $S-1$-el. Azt állítjuk, hogy

valamely $k=2,3,\dots ,2021$ értékre. Ebből világosan látszik, hogy $m\ge 3$ és így lehetségesnek kell lennie, hogy $m-1$-et felírjuk $\left\{2,3,\dots ,2021\right\}$ egy részhalmazának összegeként. Továbbá a $\{k,k+1,\dots ,2021\}$-en kívüli összes részhalmazban elég az összeg egyik tagjának értékét megnövelni $1$-el ahhoz, hogy megkapjuk $m$ lehetséges értékét. Emellett tudjuk, hogy $k\le 3$, mivel máskülönben

kifejezheti $m$-et. Ezért $m=1+3+4+\dots +2021=S-1$. Következésképp $Q(x)$-nek $\frac{S}{2}+1$ pozitív együtthatója van az $x$ páros kitevőiből és $\frac{S}{2}-2$ pozitív kitevője az $x$ páratlan kitevőiből. Az eredeti $P(x)$ polinomnak ellentétes előjelűek a páratlan kitevőihez tartozó együtthatói, így pontosan $\frac{S}{2}+1=1021616$ pozitív együtthatója van.

Eredmény:

$26550$

Először számoljuk meg, hány legövidebb út van, ha nincsen útlezárás. Hogy $(0,0,0)$-ból $(4,4,4)$-be jusson, Dávid 4 lépést tesz az $x$ koordinátatengely irányába, 4 lépést az $y$ irányba, és 4 lépést a $z$ irányba. Ha bármikor „visszafele irányba” lép, akkor a kapott útvonal már nem lesz a lehető legrövidebb. Tehát $\frac{12!}{4!\cdot 4!\cdot 4!}$ lehetséges útvonal van.

Számoljuk meg, ezek közül hány útvonal megy át a $(2,2,2)$ kereszteződésen. $(0,0,0)$-ból $(2,2,2)$-be $\frac{6!}{2!\cdot 2!\cdot 2!}$-féleképpen tud eljutni, és minden egyes útvonalat $\frac{6!}{2!\cdot 2!\cdot 2!}$-féleképeen tud folytatni $(2,2,2)$-ből $(4,4,4)$-be. Tehát összesen $\frac{6!}{2!\cdot 2!\cdot 2!}\cdot \frac{6!}{2!\cdot 2!\cdot 2!}=\frac{6!\cdot 6!}{2^6}$ útvonalat találtunk.

Ezek alapján azoknak az utaknak a száma, amelyek nem mennek át a $(2,2,2)$ kereszteződésen, $\frac{12!}{4{!}^3}-\frac{6{!}^2}{2^6}=26550.$

Eredmény:

$98$

Nevezzük el a pontokat az ábrán látható módon.

Mivel az $\mathit{ABC}$ háromszög szabályos, $\mathit{BDE}\sphericalangle +\mathit{DEB}\sphericalangle =120^{\circ }=\mathit{BDE}\sphericalangle +\mathit{FDA}\sphericalangle$, azaz $\mathit{DEB}\sphericalangle =\mathit{FDA}\sphericalangle$. Emiatt az $\mathit{ADF}$ és $\mathit{BED}$ háromszögek hasonlóak. A két háromszög területeinek aránya $100:64$, így az egymásnak megfelelő oldalak aránya $5:4$. Ha az $r=\mathit{DB},s=\mathit{BE},t=\mathit{ED}$ hosszakat használjuk, az alábbi ábrát kapjuk:

Legyen $a$ az eredeti szabályos háromszög oldalhossza, így az alábbi egyenleteket kapjuk

Az egyenletrendszer alapján $r=\frac{a}{3}$ és $s=\frac{8a}{15}$. Ezt visszahelyettesítva a (4) egyenletbe,

ahol $S$ a szabályos háromszög területe. A keresett $A$ területre teljesül, hogy $100+64+2A=360$, tehát $A=98$.

Eredmény:

$\frac{5}{8}$

Nevezzük $E$-nek az az eseményt, amikor a fej-írás-fej sorozat (röviden $\mathit{FIF}$), előbb fordul elő, mint az $\mathit{IFIF}$ és legyen $P(E)$ ennek az eseménynek a valószínűsége. Legyen $s$ a fej és írás fix véges sorozata, és jelöljük $P(E|s)$-sel annak a valószínűségét, hogy az $E$ esemény olyan sorozatban fordul elő, ami $s$-sel kezdődik és véletlenszerűen folytatódik. Legyen $x=P(E|F)$ és $y=P(E|I)$. Mivel az érme szabályos, egy vagy két lépéssel továbbhaladva (úgy, hogy a legújabb eredményt mindig az adott sorozat legvégére írjuk) megkapjuk, hogy

és ennek mintájára három lépés után megkapjuk, hogy

Mivel $\mathit{FIF}$ és $\mathit{IFIF}$ váltakozó sorok, arra jutunk, hogy

Továbbá mivel $P(E|\mathit{FIF})=1$ és $P(E|\mathit{IFIF})=0$, a (1)-es és (2)-es egyenleteket az alábbi módon átírhatjuk:

Ebből megkapjuk, hogy $x=\frac{3}{4}$ és $y=\frac{1}{2}$. A keresett valószínűség tehát $P(E)=\frac{1}{2}P(E|F)+\frac{1}{2}P(E|I)=\frac{x+y}{2}=\frac{5}{8}$.

Eredmény:

$16$

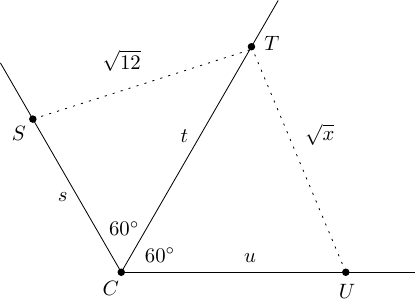
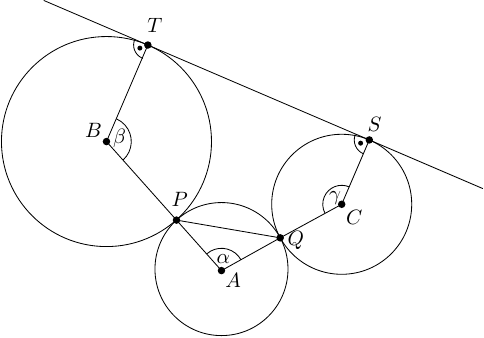
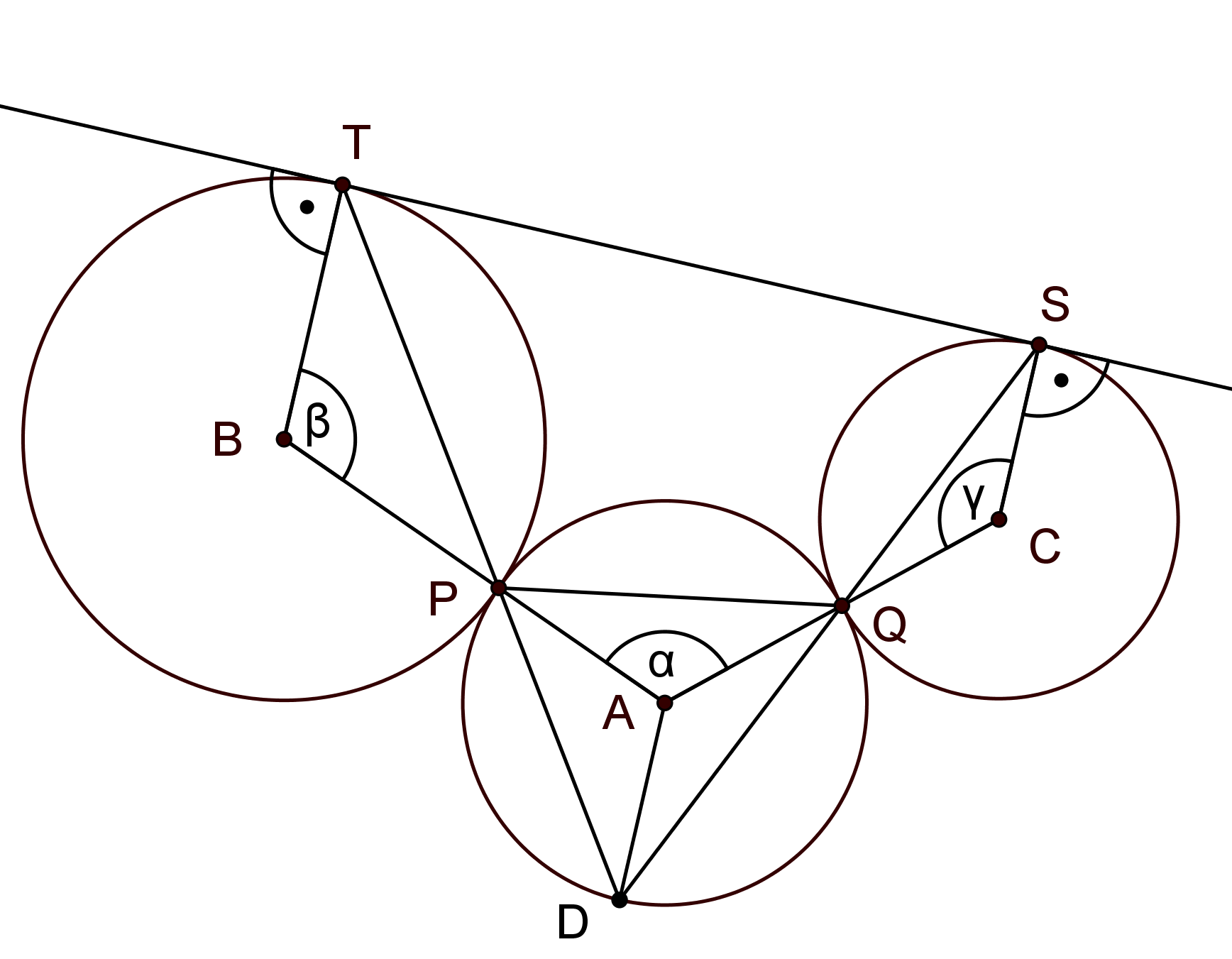
Vegyük fel a síkban az $S$, $T$, $U$ és $C$ pontokat úgy, hogy $\mathit{CS}=s$, $\mathit{CT}=t$, $\mathit{CU}=u$ és

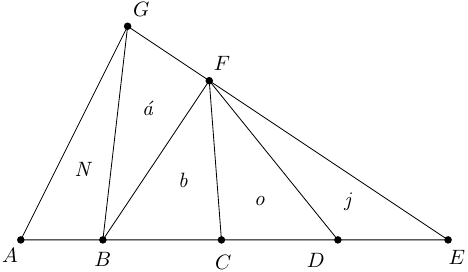
ahogy az alábbi ábra mutatja. A koszinusztörvény ($\cos 60^{\circ }=1∕2$) miatt a feladatban szereplő egyenletek alapján feltételezhetjük, hogy $S{T}^2=12$ és $T{U}^2=x$. Mivel a $T$ pont $\mathit{SC}$ szakasztól való távolsága legfeljebb $\sqrt{12}$, és akkor és csak akkor egyenlő $\sqrt{12}$-vel, ha $\mathit{TSC}\sphericalangle =90^{\circ }$, megkapjuk, hogy

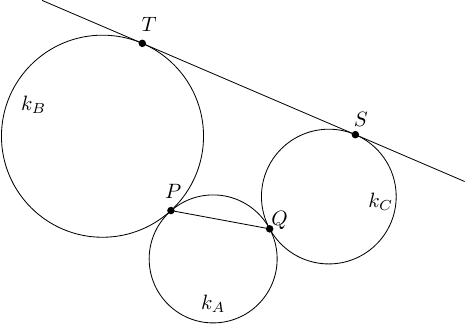
A következőkben rögzítsük a $C$ pontot és a belőle kiinduló három félegyenest, és az $S$, $T$, $U$ pontokat csak a hozzájuk tartozó félegyenesen mozgassuk! Ha $\sqrt{x}<4$, akkor el tudjuk helyezni a $\mathit{TU}$ szakaszt az $\mathit{UCT}$ szög szárai közt (vagyis találhatunk megfelelő $u$ és $t$ értékeket) úgy, hogy $\mathit{CU}<\mathit{CT}\le 4$, valamint $\mathit{CUT}\sphericalangle \ne 90^{\circ }$ (ha az $U$ pontot nagyon közel helyezzük a $C$ ponthoz). Az első egyenlőtlenségből és a szögre vonatkozó megkötésből következik, hogy a $T$ középpontú, $\sqrt{x}$ sugarú kör két pontban érinti a $\mathit{CU}$ félegyenest, $U$-ban és $U^{\prime }$-ben (lásd az alábbi ábrát), ami ellentmond az $u$ különbözőségét tiltó feltételnek. A második egyenlőtlenség azt feltételezi, hogy a $T$ középpontú, $\sqrt{12}$ sugarú kör legalább egy pontban érinti a $\mathit{CS}$ félegyenest, ami az $S$ pont. Ez a két megállapítás arra utal, hogy $x\ge 4$.

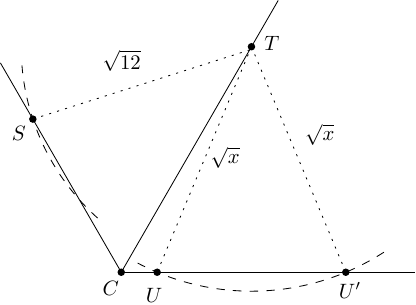
$\sqrt{x}=4$-re (és bármely más fix $\sqrt{x}\ge 4$ értékre), illetve bármely $0<t\le 4$-re csak egy ilyen $U$ érintőpont létezik, és így az említett megkötés teljesül. A fentiek mintájára a $T$ középpontú, $\sqrt{12}$ sugarú kör legalább egy $S$ pontban érinti a $\mathit{CS}$ félegyenest, és az ebből adódó $(s,t,u)=(\mathit{CS},\mathit{CT},\mathit{CU})$ számhármas behelyettesíthető az egyeenletrendszerbe, hogy megkapjuk $x$-et. Ebből következik, hogy a lehető legkisebb $x$ érték, ami megfelel a feltételeknek, $4^2=16$.