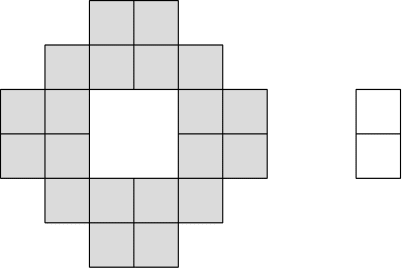
Egy épület szintes. Minden szint folyosójára két különböző ajtón lehet bejutni, és minden folyosón négy szoba található. Minden szobának saját ajtaja van, és minden szobának egy-egy lakója van. Minden ajtón, azaz a szobák és a folyosók ajtajain egy-egy zár lesz felszerelve, majd a lakók közt kulcsokat osztunk szét, úgy, hogy
- Minden lakó be tudjon jutni a saját szobájába, de máséba nem,
- Mindenki ki tudja nyitni a saját szobájához tartozó folyosót, és
- Megengedett, hogy más szintek folyosóihoz is hozzáférhessenek.
Minden zárhoz egy egyedi kulcs tartozik, és csak azzal a kulccsal lehet kinyitni. Azonban több ajtón is lehet azonos a zár, és a hozzá tartozó kulcsból is tetszőleges számú másolat készíthető. Egy lakó tetszőleges számú kulcsot kaphat. A zárak beszerelését végző cég minimalizálni szeretné a kulcsok legyártásának költségeit. Egy új kulcs legyártásának költsége 3, míg egy másolat készítése 2-be kerül. Mekkora a szétosztandó kulcsok minimális összköltsége, ha teljesíteni akarjuk a fenti feltételeket?Megoldás
Eredmény:
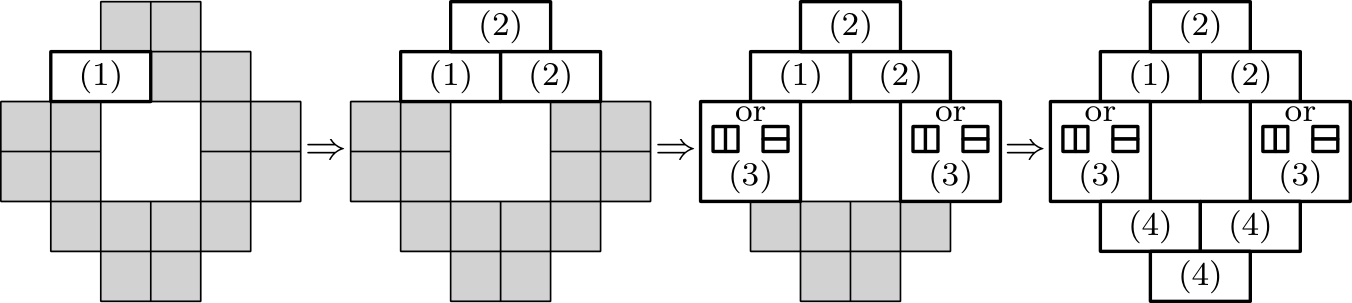
Vizsgáljuk meg a zárak és kulcsok elrendezésének legköltséghatékonyabb megoldását; egyértelmű, hogy ebben az estben semelyik lakónak nincs kettőnél több kulcsa. Továbbá az általánosság megsértése nélkül be kell látnunk, hogy mindegyik emeleten pontosan egy (vagy ekvivalensen legalább egy, mivel nem lehet egynél több) olyan lakó van, akinek csak egyetlen kulcsa van. Ez a kulcs egyben nyitja a lakó szobáját és a folyosóra vezető egyik ajtót, míg az emelet másik három lakója a másik folyosóajtót használja.
Tegyük fel, hogy valamelyik emeleten nem ez a helyzet! Ekkor az egyik folyosóajtót, melyet nevezzünk -nek, legfeljebb két lakó használja a négyből: az lakó és potenciálisan a lakó. Ha négyük közül egy lakó sem tudja kinyitni a ajtót, tetszőlegesen kiválasztunk közülük egyet, akit -két kezelünk. A következőképp változtatunk a kulcsrendszeren: kicseréljük a zárat a ajtón egy teljesen újra és ugyanezt a zárat szereljük fel az lakó ajtajára. Ezek után az lakónak csupán egy kulcsra van szüksége, melynek költsége , míg a korábbi két kulcsának együttes költsége legalább volt. Így ez a módszer legalább -gyel csökkenti az összköltséget.
Továbbá ha a lakó is érintett, akkor új folyosókulcsot osztunk neki, ami a másik folyosóajtót nyitja, amivel nem növeljük a kulcsok összköltségét. Azonban ekkor lehetséges, hogy olyan kulcspárhoz jut, ami egy másik emeleten lévő szobába ad neki bejutást; ezt elkerülvén lecseréljük a zárat szobáján egy teljesen újra, ami legfeljebb -gyel növeli az összköltséget.
Mivel a kulcsok összköltsége nem növekszik ezáltal a folyamat által, arra következtethetünk, hogy a fent meghatározott konfiguráció legalább olyan költséghatékony, mint bármely alternatívája. Ezért a következőkben azt feltételezzük, hogy minden emeleten pontosan egy lakó birtokol egy darab kulcsot.
Így a probléma arra redukálódik, hogy 160 emeleten van emeletenként egy folyosóajtó és három külön szoba, és erre kell a további költségeket minimalizálni. Legyen különböző kulcstípusunk ()! Minden lakónak kapnia kell egy kulcsot a folyosóhoz és egyet a szobájához, és ez a két kulcs nem lehet azonos típusú. Emellett semelyik két lakónak nem lehet ugyanaz a kulcspárja, mert akkor ugyanabba a szobába be tudnának menni mindketten. Ebből a kulcspárok lehetséges száma -nek adódik.
Mivel összesen kulcspárt kell kiosztanunk, alsó korlátot kapunk -re a következő egyenlőtlenségből:
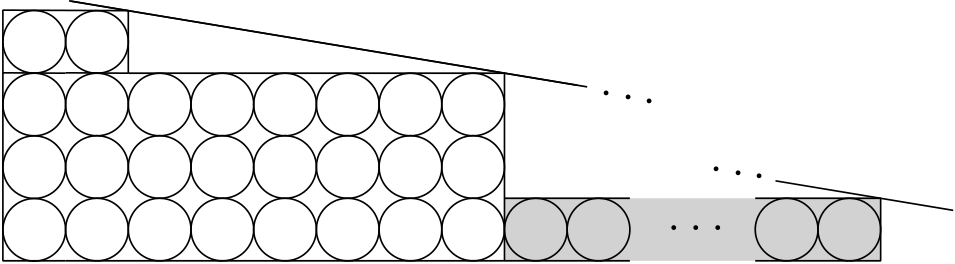
Ezt pozitív egész -ekre megoldva azt kapjuk, hogy . Most be kell látnunk, hogy megvalósítható, hogy pontosan kulcstípust használjunk. Hogy ezt elérjük, a 160 emeletet 32 csoportra osztjuk ötemeletenként. A kulcsok beosztása ekkor a következőképpen alakul (a pár első kulcsa vonatkozik a folyosóra, a második a szobára):
- Az első csoportban levő 15 lakó a kulcspárokat kapja.
- A második csoport 15 lakójának a párok jutnak.
- A minta folytatódik, a 31. csoport lakói a párokat kapják.
- Végül az utolsó (32.) csoporthoz a párokat rendeljük.
Könnyen belátható, hogy ez az elrendezés a feladat feltételeit teljesíti, így különböző típusú kulcsra van szükségünk, amihez másolatot kell adnunk, hogy megkapjuk az összesen szükséges kulcsot.
Ha pedig az első bekezdésben külön kezelt lakókat is számoljuk, összesen különböző kulcsot kell gyártani, így a végső költség .