Wynik:
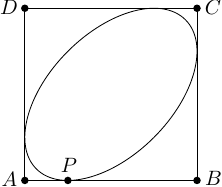
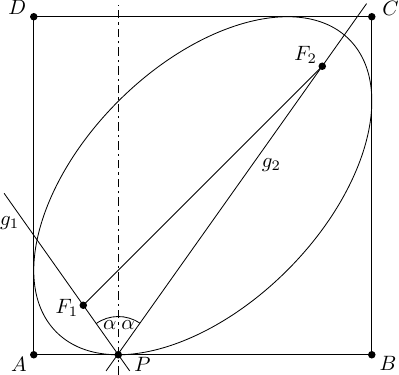
Rozwiążemy problem bardziej ogólny. Niech dany będzie kwadrat o boku długości , niech ponadto będzie środkiem układu współrzędnych. Punkt o współrzędnych leży na boku , przy czym spełnione są nierówności . Jeżeli przez oznaczymy współrzędne ogniska , to współrzędne ogniska wyrażają się wzorem (oba ogniska leżą na przekątnej symetrycznie względem drugiej przekątnej).
Oznaczamy przez prostą przechodzącą przez punkty i , jej równanie dane jest wzorem
podobnie prosta przechodzi przez punkty i , a jej równanie to
Prosta przechodząca przez punkt prostopadła do prostej jest dwusieczną kąta , dlatego współczynnik kierunkowy prostej jest liczbą przeciwną do współczynnika kierunkowego prostej . Dostajemy, że
lub równoważnie
Otrzymane równanie kwadratowe ma dwa rozwiązania , odpowiadające dwóm ogniskom elipsy. Odległość między ogniskami obliczamy korzystając z twierdzenia Pitagorasa, otrzymując . Po podstawieniu oraz dziesięciokrotnym powiększeniu dostajemy żądany wynik .
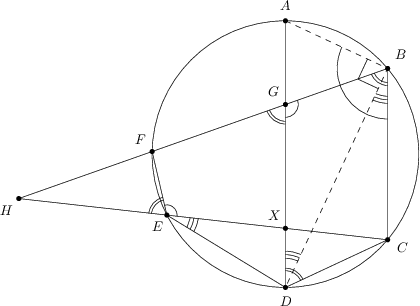
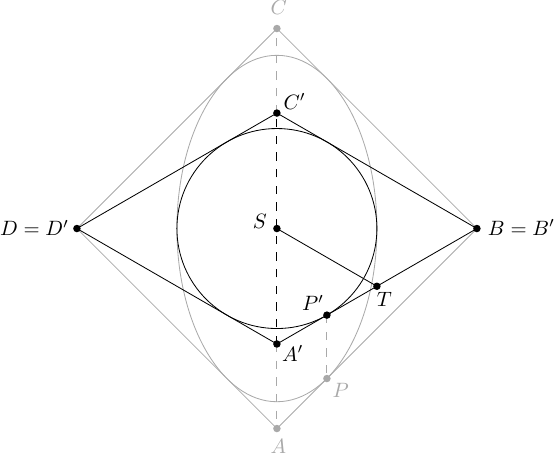
Drugie rozwiązanie. Zastosujmy przekształcenie afiniczne, polegające na zwężeniu kwadratu oraz elipsy wzdłuż przekątnej , w ten sposób aby obrazem elipsy był okrąg. Punkty po przekształceniu oznaczamy apostrofem. Niech punkt będzie środkiem odcinka , zaś punkt środkiem odcinka .
Po przekształceniu stosunki boków równoległych zostają zachowane, dlatego i w konsekwencji . W trójkącie wysokość dzieli bok na połowy, stąd . Otrzymujemy, że oraz trójkąt jest równoboczny. Wnioskujemy stąd, że nasze przekształcenie odbyło się w stosunku
Łatwo obliczyć, że promień otrzymanego okręgu (którego długość pokrywa się z długością mniejszej półosi elipsy) wynosi . Długość dłuższej półosi otrzymujemy dzieląc długość krótszej półosi przez stosunek zwężenia. Znając długości , pozostaje obliczyć mimośród ze wzoru , a następnie przemnożyć go przez dwa, aby otrzymać odległość ognisk.