Wynik:
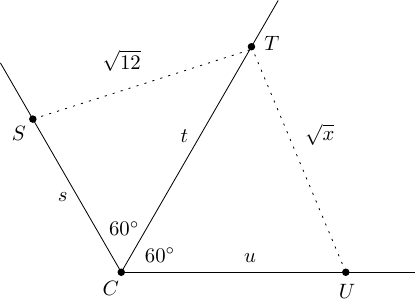
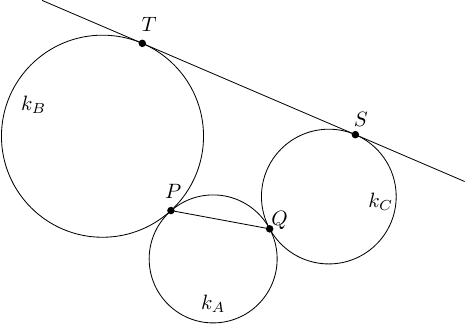
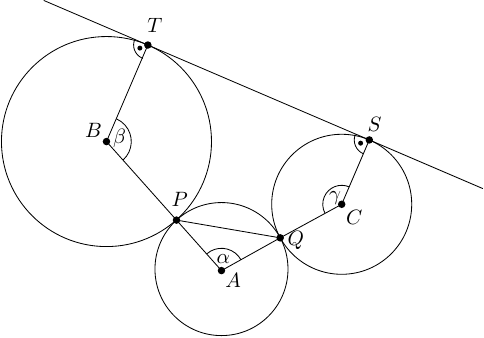
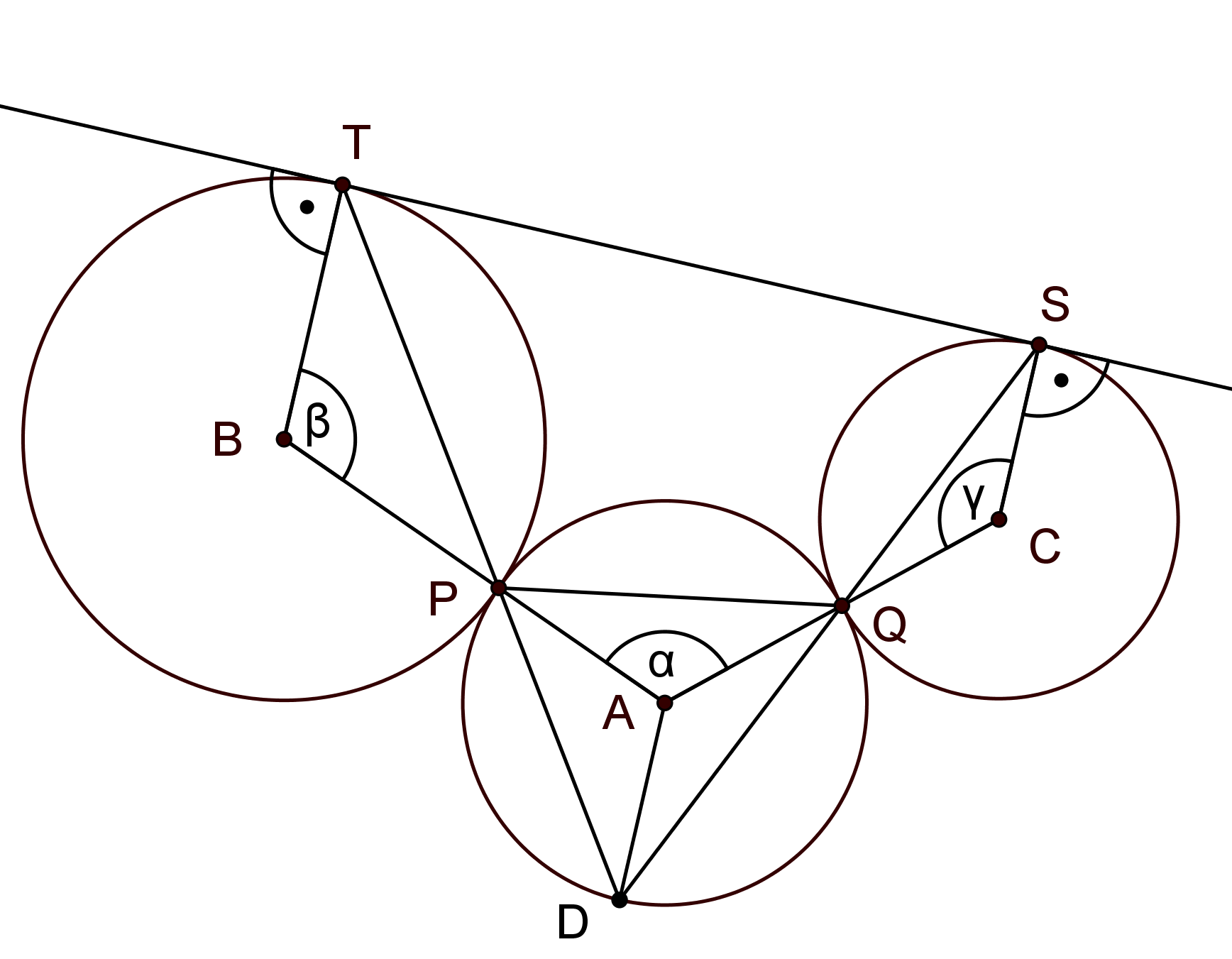
Oznaczmy środki okręgów odpowiednio przez , i . Niech , , . Skoro i , to , co wynika z obliczenia sumy kątów wewnętrznych w pięciokącie .
Ponieważ jest styczną do okręgów i , więc oraz . Skoro
to , a więc na czworokącie można opisać okrąg. Niech oznacza punkt przecięcia prostych i . Z opisywalności okręgu na otrzymujemy, że trójkąty i są podobne. Stąd
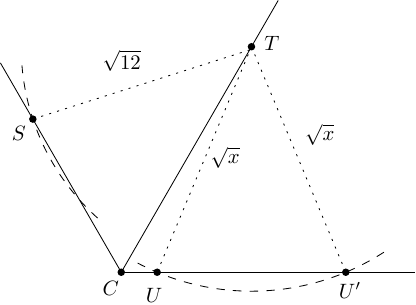
Ponownie wykorzystując równości i , wnioskujemy, że , co oznacza, iż leży na okręgu .
Wobec tego mamy , a więc trójkąty i są również podobne. Analogicznie . Podobieństwa te implikują równości
które prowadzą do równości
Łącząc otrzymane równości otrzymujemy, że
Wstawiając wartości liczbowe z treści zadania otrzymujemy równanie kwadratowe na :
które ma dwa rozwiązania:
Niemniej, tylko jedno z nich jest dodatnie, a zatem szukaną wartością jest .