Wynik:
Rozważmy optymalny pod względem kosztów układ zamków i kluczy; jasne jest, że w takim przypadku żaden mieszkaniec nie posiada więcej niż dwóch kluczy. Pokażemy ponadto, że możemy założyć bez utraty ogólności, że na każdym piętrze jest dokładnie jeden (lub równoważnie, co najmniej jeden, ponieważ nie może być więcej niż jeden) mieszkaniec, który posiada tylko jeden klucz. Ten klucz zapewnia dostęp zarówno do jego mieszkania, jak i do jednych z drzwi na korytarz, podczas gdy pozostali trzej mieszkańcy tego piętra korzystają z drugich drzwi na korytarz.
Załóżmy, że nie jest tak na pewnym piętrze. Wtedy jedne z drzwi wejściowych na korytarz, , są używane przez co najwyżej dwóch z czterech mieszkańców – mieszkańca i ewentualnie mieszkańca . Jeśli żaden z czterech mieszkańców nie może otworzyć , wybieramy jednego z nich arbitralnie i traktujemy dalej jako . Modyfikujemy system kluczy w następujący sposób: wymieniamy zamek w drzwiach na zupełnie nowy i instalujemy ten sam zamek w drzwiach pokoju . W rezultacie potrzebuje teraz tylko jednego klucza, który kosztuje , podczas gdy poprzednie dwa klucze miały łączny koszt co najmniej . To zmniejsza całkowity koszt o co najmniej .
Co więcej, jeśli mieszkaniec istnieje, przypisujemy mu klucz do korytarza tak, aby pasował do innych drzwi korytarza na tym piętrze, co nie zwiększa całkowitego kosztu. Jednak w ten sposób może skończyć z kombinacją kluczy umożliwiającą dostęp do mieszkania na innym piętrze; aby to naprawić, wymieniamy zamek w mieszkaniu na zupełnie nowy, co zwiększa koszt maksymalnie o .
Ponieważ całkowity koszt nie wzrasta w trakcie tego procesu, wnioskujemy, że założona konfiguracja jest co najmniej tak opłacalna, jak każda inna. Dlatego w dalszej części zakładamy, że na każdym piętrze jest dokładnie jeden mieszkaniec z jednym kluczem.
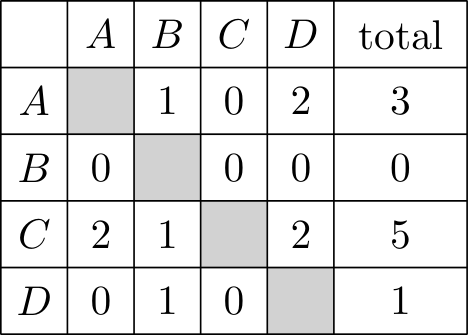
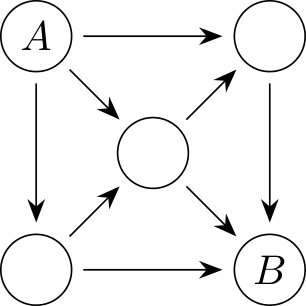
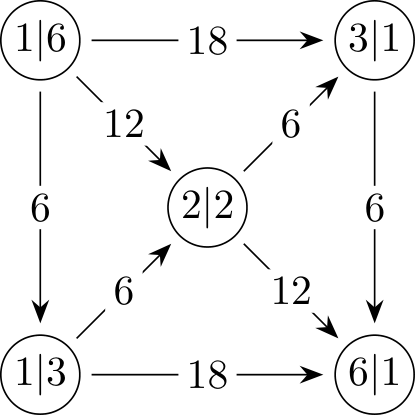
W ten sposób problem sprowadza się do minimalizacji kosztu klucza dla 160 pięter, gdzie każdy korytarz ma tylko jedno wejście i trzy oddzielne mieszkania. Niech będzie różnych typów kluczy . Każdy mieszkaniec otrzymuje jeden klucz do swojego mieszkania i jeden klucz do korytarza, a te dwa klucze nie mogą być tego samego typu. Ponadto, dwaj mieszkańcy nie mogą mieć tej samej pary typów kluczy, ponieważ oznaczałoby to, że mają dostęp do tego samego pokoju. Dlatego liczba prawidłowych par kluczy wynosi .
Ponieważ rozprowadzamy łącznie par kluczy, wyznaczamy dolne oszacowanie dla z nierówności
Rozwiązując równanie dla dodatniej liczby całkowitej , znajdujemy . Teraz pokażemy, że możliwe jest użycie dokładnie różnych typów kluczy. Aby to osiągnąć, dzielimy 160 pięter na 32 grupy po 5 pięter każda. Przypisanie kluczy przebiega następująco (pierwszy klucz w parze jest dla korytarza, a drugi dla mieszkania):
- W pierwszej grupie mieszkańców otrzymuje następujące pary kluczy: .
- W drugiej grupie przypisujemy pary kluczy: .
- Kontynuujemy rozdawanie kluczy w taki sposób jak powyżej, wtedy mieszkańcy z grupy otrzymują pary kluczy: .
- Ostatnia ( grupa) otrzymuje następujące pary kluczy: .
Łatwo zauważyć, że ten rozkład spełnia podane powyżej warunki. Dlatego jest minimalną wymaganą liczbą unikalnych kluczy, do której dodajemy kopii, aby mieć wszystkie kluczy.
Uwzględniając mieszkańców posiadających tylko jeden klucz, należy wyprodukować łącznie unikalne klucze. Tak więc ostateczny koszt wynosi .