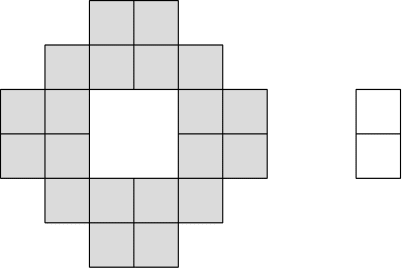
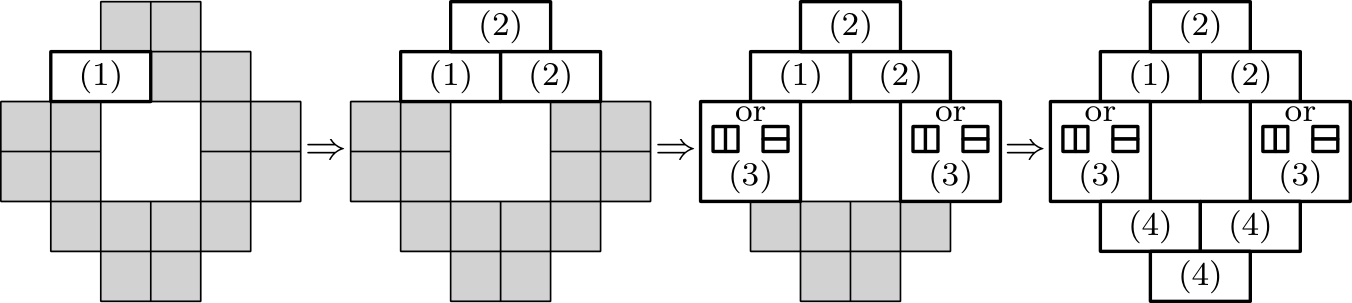
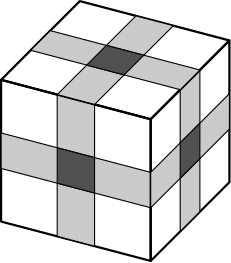
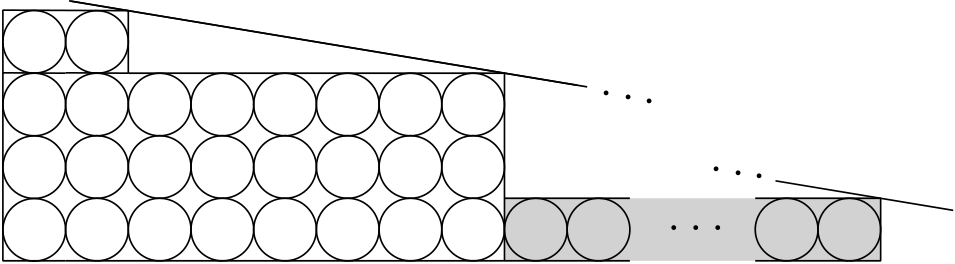
Um edifício tem 160 pisos. O corredor de cada piso é acessível através de duas portas principais, e o corredor contém quatro quartos. Cada quarto tem a sua própria porta, com uma pessoa a residir em cada quarto. Será instalada uma fechadura única em cada porta, incluindo as portas dos corredores, e as chaves serão distribuídas de forma a assegurar que:
- Cada pessoa pode aceder apenas ao seu próprio quarto, não aos dos outros;
- Cada pessoa pode aceder ao corredor do seu piso; e
- É permitido que alguém tenha acesso a corredores de outros pisos.
Cada fechadura está associada a uma chave única e só pode ser aberta por essa chave. Contudo, a mesma fechadura pode ser utilizada em várias portas, se necessário, e podem ser feitas cópias ilimitadas da sua respetiva chave. Cada pessoa pode possuir tantas chaves quantas sejam necessárias. A empresa responsável pela instalação pretende minimizar o custo total de produção das chaves. Fabricar uma nova chave custa 3, e fazer uma cópia de uma chave existente custa 2. Qual é o custo total mínimo de todas as chaves, cumprindo as condições acima?Solução
Resposta:
Para minimizar os custos, nota-se que se um residente tiver uma única chave única que abra tanto o seu quarto como uma porta do corredor, é mais económico do que ter duas chaves separadas (mesmo que estas sejam apenas cópias). Contudo, esse arranjo implica que uma porta do corredor deve permanecer inacessível aos outros, pois partilhar o acesso a essa porta concederia, também, acesso ao quarto desse residente.
Assim, o problema reduz-se a minimizar o custo das chaves para 160 pisos, onde cada corredor tem apenas uma entrada e três quartos distintos. Seja o número de tipos distintos de chaves, . Cada residente recebe uma chave para o seu quarto e uma para o corredor. Essas duas chaves não podem ser do mesmo tipo; de facto, se a chave do quarto de um residente fosse igual à chave do corredor, os outros dois residentes que partilhassem a chave do corredor teriam acesso ao quarto desse residente ou ficariam impossibilitados de aceder ao corredor. Além disso, nenhum par de residentes pode ter o mesmo par de tipos de chave, pois isso significaria que teriam acesso ao mesmo quarto. Assim, o número de pares de chaves válidos é dado por .
Como serão distribuídos um total de pares de chaves, determina-se um limite inferior para a partir da desigualdade
Resolvendo para inteiro positivo, verifica-se que . Agora, demonstra-se que é possível usar exatamente tipos distintos de chaves. Para tal, divide-se os 160 pisos em 32 grupos de 5 pisos cada. A atribuição das chaves procede da seguinte forma (a primeira chave do par é para o corredor e a segunda para o quarto):
- Os 15 residentes do primeiro grupo recebem os pares de chaves .
- Ao segundo grupo são atribuídos os pares .
- Este padrão continua, sendo que o 31º grupo recebe os pares .
- Finalmente, o último grupo (32º) recebe os pares .
É fácil verificar que esta distribuição satisfaz as condições impostas. Portanto, é o número mínimo de chaves difererentes necessárias, ao que se adicionam 928 cópias para cobrir todas as chaves.
Considerando os residentes mencionados no primeiro parágrafo, é necessário produzir, no total, chaves originais. Assim, o custo final é calculado como .