Enunțuri probleme

Răspuns:

4444

Îndoind colțurile "interioare" în "exterior", decagonul se transformă într-un dreptunghi de dimensiuni $2018$ și $70+134=204$. De aceea perimetrul este $2\cdot (2018+204)=4444$.

Răspuns:

$34$

Deoarece orarul parcurge $360^{\circ }:12=30^{\circ }$într-o oră, în 2 minute parcurge $1^{\circ }$. De aceea, a parcurs $137^{\circ }-4\cdot 30^{\circ }=17^{\circ }$ după ora 4, deci au trecut $17\cdot 2=34$ minute.

Răspuns:

18

Se poate observa că dacă pampam înseamnă mai mare, atunci Kevin are cel mai mare punctaj și Liam are cel mai mic punctaj și, dacă pampam înseamnă mai mic, atunci situația este inversă. În oricare situație, Madison și Natalie mereu vor avea punctajele din mijloc, adică 6 și 12. De aceea suma punctajelor celor doi este 18.

Răspuns:

17

Deoarece casa 4 a lui Jack este casa cu numărul 16 a lui John, există un segment de case unde numărul caselor lui John este mai mare cu 12. Acest segment de case trebuie să se termine înainte ca Jack să ajungă la casa cu numărul 12, deoarece, altfel, John ar obține $12+12=24$. Din cauză că întotdeauna numărul scade cu numărul total de case atunci când se ajunge la finalul numărării, observăm că sunt $24-7=17$ case în piață.

Răspuns:

$19$

În instrucțiuni, soluția este obținută din $1$ parte oțet și $5$ părți apă. Aceeași soluției se obține din $1$ parte oțet de concentrație $40\%=4\cdot 10\%$ și $4\cdot 5=20$ părți apă. Deci sunt necesare $19$ extra părți de apă.

Răspuns:

$110^{\circ }$

Se consideră punctele $D$, $E$ pe $h$, respectiv $g$, astfel încât $\mathit{ED}$ este perpendiculară pe cele două drepte, formându-se pentagonul $\mathit{ABCDE}$. Cum suma unghiurilor unui pentagon este $540^{\circ }$, măsura unghiului căutat este $540^{\circ }-180^{\circ }-105^{\circ }-145^{\circ }=110^{\circ }$.

Răspuns:

$67.5^{\circ }$

Fie $X$, $Y$ notații pentru unghiurile de măsură $𝜀$. Atunci $\mathit{\angle AXY}=\mathit{\angle AY}X=𝜀$. Deoarece $\mathit{\angle XAY}=\mathit{\angle CAB}=45^{\circ }$, din suma unghiurilor triunghiului $\mathit{XY}A$ obținem

adică $𝜀=67.5^{\circ }$.

Răspuns:

$7$

Fie $c$ vârsta lui Cederic și $m$ vârsta mamei, $c$ fiind egal cu $m$ citit invers. Numerele $c$ și $m$ au același număr de cifre (presupunem că $c$ este posibil să înceapă cu cifra zero, dacă $m$ are cifra unităților zero), care este cel puțin $2$. Fie $a$ și $b$ cifrele unităților numerelor $c$ și, respectiv $m$. Cum mama lui Cederic are $27$ de ani, se observă că putem avea $a+7=b$ sau $a+7=10+b$. Dacă vârsta mamei ar fi cel puțin egală cu $100$, diferența dintre primele cifre ale vârstelor lor poate fi cel mult $1$, ceea ce nu este posibil, deoarece ele sunt exact cifrele $b$ și $a$. În concluzie, numerele $c$ și $m$ au $2$ cifre.

Dorim să aflăm toate numerele $\overline{\mathit{ab}}$ astfel încât

Știm că $a>b$, deci condiția $a+7=b$ nu este adevărată. Din relația $a+7=10+b$ obținem $a=b+3$. Deoarece $a\le 9$, obținem că $b\le 6$. Pentru fiecare cifră $b\in \{0,1,\dots ,6\}$, obținem cifra $a$ astfel încât $a=b+3$. Se observă ușor că pentru aceste cifre relația $\overline{(b+3)b}=\overline{b(b+3)}+27$ este adevărată. Situația cerută se poate întâmpla de $7$ ori: când Cederic are $3$, $14$, $25$, $36$, $47$, $58$ și $69$ ani.

Răspuns:

$3∕4$

Dacă un cubuleț este așezat într-un colț, atunci trei dintre fețele sale sunt vizibile. Dacă este așezat pe muchia cubului mare, două fețe sunt vizibile, iar dacă este așezat în interiorul unei fețe laterale a cubului mare doar o față este vizibilă. Cum sunt opt colțuri și pe fiecare muchie mai putem pune încă două cubulețe, obținem $32$ locuri în care putem plasa cubulețele albe, obținând astfel raportul maxim cerut. În acest fel fiecare față laterală a cubului mare arată identic, având doisprezece fețe albe și patru negre. De aceea valoarea raportului este $12∕16=3∕4$.

Răspuns:

3

Deoarece nimeni nu a picat și testul psihologic și testul de experiență profesională, toți participanții care au picat la cel puțin două teste au ratat misiunea din cauza testului de sănătate. Astfel $(100-26)-60=14$ persoane au picat doar testul de sănătate. Cum $83$ persoane au picat fie testul psihologic, fie testul de experiență profesională, obținem $97$ de persoane care au picat cel puțin un test, deci doar $3$ astronauți au fost selectați.

Răspuns:

$5:4$

Fie $s$ lungimea laturii pătratului $B$. Observăm din simetrie că centrul cercului se află pe mijlocul laturii pătratului $B$, împărțind-o pe aceasta în două părți de lungime $s∕2$. Din teorema lui Pitagora, obținem

de unde raportul cerut este $5:4$.

Răspuns:

$10$

Cum în produs avem $2\cdot 5$, ultima cifră este $0$. Cifra zecilor se obține din ultima cifră a produsului $3\cdot 7\cdot 11\cdot \dots \cdot 37$. Este suficient să folosim ultima cifră din fiecare rezultat obținut în urma unei înmulțiri. Mai mult, putem ignora cifra unu dacă este ultima cifră. Deci va trebui să determinăm ultima cifră a produsului

Cum $3\cdot 7=21$ are ultima cifră $1$, putem omite perechile de $3$ și $7$. Rămânem cu $9\cdot 9$, care are ultima cifră $1$. În concluzie, ultimele două zecimale sunt $10$.

Răspuns:

3

Fie $n$ numărul de prieteni ai ultimului suspect. Suspectul cu cinci prieteni este prieten cu toți ceilalți, deci prin omiterea acestuia, numărul de prieteni al celorlalți scade cu unu. Atunci îl omitem și pe cel care avea un singur prieten deoarece numărul său de prieteni a scăzut la zero. În acest fel am obținut un grup de patru suspecți, despre care știm că au $1$, $2$, $3$, și $n-1$ prieteni printre ei. Repetând ultimii doi pași, obținem un grup și mai mic cu valorile $1$ și $n-2$; este evident acum că $n-2=1$, adică $n=3$.

Notă: Soluția problemei se poate obține și din diagrama următoare:

Răspuns:

40

Fie $P$ rezultatul numerelor de pe fețele opuse. În mod evident, cu cât $P$ este mai mare, cu atât este mai mare suma totală. Din moment ce $P$ trebuie să fie divizibil cu toate cele trei numere afișate, valoarea cea mai mică a lui $P$ este cel mai mic multiplu comun, $P=36$. În aceste condiții, numerele afișate pe celelalte fețe sunt $3$, $4$ și $6$, iar suma cerută este de $6+9+12+6+4+3=40$.

Răspuns:

$99^{\circ }$

Notăm anumite vârfuri ca în figură.

Unghiul $\mathit{CBD}$ este diferența dintre unghiurile interioare ale octogonului și pentagonului, deci $\mathit{\angle CBD}=135^{\circ }-108^{\circ }=27^{\circ }$. Se obține ușor că $\mathit{\angle ABD}=135^{\circ }$. Cum triunghiurile $\mathit{ABD}$ și $\mathit{CBD}$ sunt isoscele,

De aceea

Răspuns:

50

Timpul pe care ministrul l-a câștigat trezindu-se mai devreme (1 oră) îl împărțim în timpul necesar parcurgerii distanței necunoscute $t$ și timpul rămas mașinii de a parcurge distanța de la punctul de întâlnire la casa ministrului, care este jumătate din timpul salvat, adică

de unde $t=50$.

Răspuns:

725

Fie $d$ prima cifră a numărului, $k$ numărul obținut după eliminarea primei cifre, și $n$ numărul de cifre al numărului $k$. Atunci numărul inițial este egal cu $10^{n}d+k$ și ipoteza se poate scrie

sau

Cum $28=2^2\cdot 7$, și membrul drept trebuie să se dividă cu $28$, obținem $d=7$ și $n\ge 2$. Alegerea $n=2$ (implică $k=25$) oferă cel mai mic număr natural $725$.

Răspuns:

44

Minutarul face 24 de rotații în 24 de ore, iar orarul face 2 rotații în 24 de ore. Din aceste motiv, minutarul se suprapune cu orarul de 22 ori în 24 de ore. În cele 22 de suprapuneri minutarul este perpendicular pe orar de 2 ori, de aceea răspunsul este 44.

Răspuns:

1111, 1221

Fie $\overline{\mathit{abba}}$ un număr palindrom. Cum el se scrie ca sumă de două numere palindrom de trei cifre, acesta nu poate fi mai mare ca $1998$, deci $a=1$. Dacă $\overline{1\mathit{bb}1}$ este egal cu $\overline{\mathit{cdc}}+\overline{\mathit{xyx}}$, atunci

Cum numărul din membrul stâng se termină cu cifra $1$, $c+x$ se termină cu cifra unu. Cum $c$ și $x$ sunt cifre diferite de $0$, $c+x=11$. Prin înlocuire, obținem

Cum $d$ și $y$ sunt cifre, membrul drept nu depășește $18$, deci $b-1$ este $0$ sau $1$. Ambele opțiuni sunt posibile: $1111=505+606$, $1221=565+656$.

Răspuns:

$31∕49$

Aria unui triunghi mic, din cele trei formate, este

din aria triunghiului mare echilateral, deoarece înălțimea este $1∕7$ și baza $6∕7$ din laturile corespunzătoare triunghiului mare. De aceea raportul dintre aria triunghiului mic echilateral și aria triunghiului mare echilateral este

Răspuns:

$(2,3,2,1)$, $(3,1,3,1)$

Un număr nu poate să apară în tabel mai mult de cinci ori; oricum, numărul cinci nu poate să apară, deoarece ar ocupa o poziție a numărului ce apare de cinci ori. Deci, doar numerele $1$, $2$, $3$, și $4$ pot să apară.

Să arătăm că $d=1$: Dacă $d=2$, atunci unul dintre numerele $a$, $b$, $c$ trebuie să fie $4$, și cum rămân doar două locuri libere, ar trebui să fie $b$. $(2,4,2,2)$ nu este un cvadruplu valid. Alegerile $d=3$ și $d=4$ ne conduc și mai repede la contradicții.

În concluzie, $a\in \{2,3\}$. Presupunând că $a=2$, obținem $b,c\in \{2,3\}$ (nu mai putem avea alți unu și patru), dar $b=2$ ar contrazice condiția lui $b$ (ar fi trei de doi), deci $b=3$, și $c=2$. Dacă $a=3$, ar trebui să avem în tabel încă un unu, și acesta nu poate să fie $c$ (deja există un alt trei), deci $b=1$, și $c=3$ .

Răspuns:

2030

În primul rând, considerăm cazul în care cele două cuvinte nu au litere în comun. Există două posibilități de alăturare a acestora: dramamate și matedrama.

Dacă au litere în comun, atunci există o singură posibilitate, și anume: dramate. Există doar trei posibilități de a alege literele lipsă: ’**dramate’, ’*dramate*’, ’dramate**’. În fiecare caz există $26^2=676$ moduri de a alege cele două litere. De aceea, în aceste situații sunt $676\cdot 3=2028$ parole posibile.

În total, există $2028+2=2030$ parole posibile.

Răspuns:

$42$

Sunt $n-1$ perechi de numere consecutive în mulțimea $\{1,2,3,\dots ,n-1,n\}$ și sunt $\frac{1}{2}n(n-1)$ posibilități de a alege două numere diferite. Obținem

de unde $n=42$.

Răspuns:

20

Observăm că, de fiecare dată când Charlie câștigă o rundă, nu are niciun impact asupra numărului de runde câștigate de Arthur sau Ben, nici nu are niciun impact asupra numărului de runde când Charlie nu joacă. Prin urmare, putem presupune că Charlie întotdeauna pierde. Cu alte cuvinte, fiecare victorie a lui Arthur împotriva lui Ben crește scorul general al lui Arthur cu două victorii (dacă nu s-a întâmplat în ultima rundă) și invers. Din moment ce numărul victoriilor lui Arthur este impar, concluzionăm că ultima rundă împotriva lui Arthur sau Ben, este câștigată de Arthur. Prin urmare, dacă vom adăuga încă o rundă (Arthur împotriva lui Charlie, câștigată de Arthur), numărul total de runde când Charlie nu ar juca ar fi o jumătate din suma finală a scorurilor lui Arthur și Ben, adică $(18+22)∕2=20$.

Răspuns:

52

Notăm cu $k$ numărul inițial de rating-uri și cu $x$ suma lor. Notăm cu $a$, $b$ rating-urile din ultima săptămână. Atunci

adică

Ecuația $(1)$ implică faptul că $k$ este multiplu de $50$. Prin scăderea relației $(1)$ din relația $(2)$, obținem

Cum $a,b\le 5$, membrul stâng este un număr natural mai mic ca $3$, deci $k\le 75$. Concluzionăm $k=50$, deci $52$ de persoane au evaluat produsul.

Răspuns:

9

Vom folosi numerele 1, 2, 3, 4 în loc de numele zilelor. Observăm că în fiecare zi sunt atribuite trei numere distincte: Numărul real al zilei și cele două numere ale șosetelor purtate. Prin urmare, putem descrie în mod echivalent atribuirea șosetelor cu un singur număr pentru fiecare zi - singurul număr din cele patru care nu apare în triplele menționate mai sus. Se deduce că asignările valide ale șosetelor corespund permutărilor $(1,2,3,4)$ care nu lasă niciunul din numere în poziția inițială.

Numărul de rearanjări poate fi calculat după cum urmează: există trei opțiuni de plasare a lui 1, lăsându-i poziția $n\ne 1$. Acum, $n$ are și trei opțiuni pentru a fi puse. Este ușor de văzut că celelalte două numere sunt acum atribuite într-un mod unic, deci există $3\cdot 3=9$ rearanjări și același număr de alegeri ale șosetelor lui Juliette.

Răspuns:

21

În total au fost $26\cdot 5=130$ de voturi. Dacă un film a primit $20$ sau mai puține voturi, celelalte $110$ voturi rămase pot fi ușor distribuite astfel încât să fie cinci filme care primesc fiecare câte $21$ de voturi. Dacă un film primește cel puțin $21$ de voturi, atunci ca să nu fie nominalizat ar implica ca alte cinci filme să primească cel puțin $22$ de voturi, obținându-se astfel cel puțin $21+5\cdot 22=131$ de voturi, deci o contradicție.

Răspuns:

$\frac{4}{7}$

Alegând $x=-2$, obținem $f(-2)-2f(3)=-2$. Alegând $x=3$, obținem $f(3)+3f(-2)=3$. Avem astfel două ecuații liniare cu necunoscutele $f(-2)$ și $f(3)$. Prin înmulțirea celei de a doua ecuații cu $2$ și adunarea acesteia la prima, obținem $f(-2)=\frac{4}{7}$.

Răspuns:

$471$

Prin descompunerea în factori primi obținem $4420=2\cdot 2\cdot 5\cdot 13\cdot 17$. Cum $13$ și $17$ sunt numere prime, unul dintre numerele $n$, $a$, $b$, $o$, $j$ trebuie să fie divizibil $13$ și altul cu $17$. Cum cel mai mic multiplu comun al numerelor $13$ și $17$ este $221$, nu există un număr de două cifre divizibil prin ambele. Fără a pierde generalitatea, putem presupune că $n$ este divizibil cu $17$ și $a$ este divizibil cu $13$. Astfel $n\le 85=5\cdot 17$ și $a\le 91=7\cdot 13$.

Deci $n=85$ și $a=91$. Cum $n=85$ este divizibil cu $5$, trebuie să ne mai asigurăm de divizibilitatea cu $4$. Dar $n$ și $a$ sunt impare, deci $4$ trebuie să dividă $\mathit{boj}$. De aceea, unul dintre numerele $b$, $o$, $j$ este divizibil cu $4$, sau două dintre numere sunt divizibile cu $2$. Suma mai mare se obține în a doua situație, când $b=o=98$ și $j=99$. Suma cerută este $n+a+b+o+j=85+91+98+98+99=471$.

În final, să verificăm posibilitățile $n<85$ sau $a<91$. Deoarece numerele $n$ și $a$ se divid cu $17$ și, respectiv $13$, ar însemna că $n\le 68=85-17$ sau $a\le 78=91-13$. Atunci suma $n+a+b+o+j$ ar putea fi cel mult $68+91+3\cdot 99=456$ (în primul caz) sau $85+78+3\cdot 99=460$ (în al doilea caz), adică mai mică decât cea obținută anterior.

Răspuns:

$10(1+\sqrt{3})$

Diagonala cutiei trece prin centrele mingii de handbal și a două mingi de tenis, precum și prin punctele de tangență ale acestor trei mingi. Singura zonă în care diagonala nu este în interiorul unei mingi sunt segmentele dintre o minge de tenis și un colț al cutiei; distanța de la centrul unei mingi de tenis la colț este jumătate din diagonala cubului circumscris mingii. Deci, lungimea diagonalei cutiei este suma

• ($2\times$) $1∕2$ din diagonala unui cub circumscris unei mingi de tenis,
• ($2\times$) raza unei mingi de tenis,
• diametrul mingii de handbal.

Astfel, diagonala cutiei este egală cu

și lungimea muchiei cutiei este egală cu

Răspuns:

$4$

Pe de o parte, puterea $2^{29}$ se poate calcula: spre exemplu, folosim $2^{10}=1024$, calculăm $1024^2$ și $1024^2\cdot 1024$. În final, împărțim rezultatul prin $2$ și obținem $2^{29}=536870912$.

Pe de altă parte, putem folosi faptul că un număr întreg și suma cifrelor sale au același rest modulo $9$. În plus, $2^n$ (mod9) este periodic de lungime $6$. Cum suma tuturor cifrelor este $45$, obținem

unde cu $x$ este notată cifra lipsă din scrierea zecimală a puterii $2^{29}$. Obținem $x\equiv 4mod9$. Deci, cifra lipsă este $4$.

Răspuns:

2501

Notăm cu $\mathrm{ftd}(n)$ primele două zecimale după punctul zecimal ale numărului $\sqrt{n}$. Este evident că dacă $n$ crește de la un pătrat perfect la altul, $\mathrm{ftd}(n)$ crește de asemenea; cum suntem interesați de cel mai mic număr natural $n$, acesta trebuie să fie de forma $k^2+1$, unde $k$ este un număr natural.

Când $\sqrt{k^2+1}$ este rotunjit la partea sa întreagă, rezultatul este $k$, de aceea $\sqrt{k^2+1}-k$ este un număr cuprins între $0$ și $1$. Afirmația $\mathrm{ftd}(k^2+1)=0$ este echivalentă cu

Adunând $k$ în ambele părți ale relației, ridicând la pătrat (ambii membri sunt pozitivi) și separând $k$ obținem

Membrul drept este un număr cuprins între $49$ și $50$; cum $k$ este număr natural, obținem $k\ge 50$. În concluzie, $n=50^2+1=2501$ este cel mai mic număr natural căutat.

Răspuns:

$9^{8068}$

Umplerea celor 8068 de celule de pe ultimele două rânduri și primele două coloane ale tablei ne oferă o idee de scriere a numerelor în celulele rămase prin umplerea celulelor de pe diagonale consecutive —vezi desenul. Pe de altă parte, este evident că, fiecare umplere corectă induce o umplere a celor 8068 celule. Prin urmare, numărul de umpleri arbitrare a acelor celule este același cu numărul dorit de umpleri corecte ale tabelului.

Răspuns:

$(3,18)$, $(6,66)$

Ecuația dată este echivalentă cu $m^2-{(2^n)}^2=260$ care prin factorizarea membrului stâng conduce la $(m-2^n)(m+2^n)=260$. Descompunerea în factori primi a numărului $260=2^2\cdot 5\cdot 13$ presupune alegerea următoarelor situații:

ținând cont că $(m-2^n)<(m+2^n)$. Deoarece $(m+2^n)-(m-2^n)=2^{n+1}$, obținem două cazuri $26-10=2^4$ și $130-2=2^7$, de unde obținem perechile $(3,18)$ și $(6,66)$, care respectă condiția dată.

Răspuns:

4033

În loc să reflectăm raza de lumină, o vom lăsa să meargă drept și reflectăm triunghiul de-a lungul laturii cu care raza este incidentă. Să arătăm că un rând al acestor triunghiuri reflectate este suficient pentru ca raza de lumină să ajungă la un vârf al unuia dintre triunghiuri.

Fie $E$ punctul de intersecție al razei $\mathit{BD}$ cu dreapta ce trece prin $A$ și este paralelă cu $\mathit{BC}$ și, $F$ un punct pe $\mathit{BC}$ astfel încât $\mathit{EF}\parallel \mathit{AC}$. Atunci triunghiurile $\mathit{BCD}$ și $\mathit{BFE}$ sunt asemenea și $\mathit{BF}=2018\mathit{BC}$. Acest lucru implică faptul că punctul $E$ este obținut prin reflexia triunghiului $\mathit{ABC}$ și că este primul punct astfel obținut pe $\mathit{BD}$.

Se observă ușor că segmentul $\mathit{BE}$ intersectează $2\cdot 2017-1=4033$ laturi de triunghiuri reflectate, care reprezintă numărul de reflexii al razei de lumină. Figura ilustrează solutia problemei cu condiția inițială schimbată în $\mathit{DC}:\mathit{AC}=1:5$.

Răspuns:

$9∕4$

Notăm punctele de intersecție ca în figură.

Triunghiurile $\mathit{KM}{D}^{\prime }$, $A^{\prime }\mathit{MC}$, și $L{A}^{\prime }B$ sunt dreptunghice și asemenea, unghiurile congruente fiind marcate pe figură, de aceea vom determine raportul de asemănare dintre două astfel de triunghiuri. Ținând cont de $\mathit{KD}=K{D}^{\prime }$ și $\mathit{LA}=L{A}^{\prime }$, obținem

și

Deoarece $A^{\prime }L$ corespunde lui $\mathit{KM}$ și $\mathit{LB}$ corespunde lui $K{D}^{\prime }$ în asemănarea menționată mai sus, obținem raportul de asemănare $3∕2$. Cum ne interesează raportul ariilor, rezultatul este ${(3∕2)}^2=9∕4$.

Răspuns:

$185$

Polinomul se poate scrie

Dar, cum

observăm că toate parantezele din membrul drept al egalității se divid cu $x^2-1$. Cum gradul polinomului $6x+1$ este mai mic decât gradul polinomului $x^2-1$, concluzionăm că $6x+1$ este restul căutat. Rezolvând ecuația $1111=6x+1$ obținem răspunsul $x=185$.

Răspuns:

$30$

Observăm că dacă distribuim liniile din pentagonul exterior, două companii (notate $X$ și $Y$) vor primi două linii și o companie ($Z$) doar o linie. Companiile trebuie să fie în ordinea $\mathit{XY}\mathit{XY}Z$ începând de la un anumit oraș. Se arată simplu că, după ce am atribuit aceste linii, restul de linii se vor atribui în mod unic: liniile pentagonului interior sunt atribuite acelorași companii în același mod ca al omologilor lor exteriori și liniile de conectare dintre pentagoane se vor atribui la compania nefolosită.

Aceasta înseamnă că numărul de distribuiri corecte al întregii rețele este egal cu numărul de distribuiri ale pentagonului exterior. Există șase modalități de a aloca cele trei companii la $X$, $Y$ și $Z$ și cinci posibilități pentru orașul în care începe alocarea $\mathit{XY}\mathit{XY}Z$. Obținem $5\cdot 6=30$ moduri în total.

Răspuns:

$25-13\sqrt{2}$

Considerăm triunghiul ale cărui vârfuri sunt centrele cercurilor din colțuri. Aceste este un triunghi dreptunghic de catete de lungimi $14$ și, respectiv $34$; din teorema lui Pitagora, lungimea ipotenuzei este

În plus, raza cercului înscris în acest triunghi poate fi determinată și este egală cu $(14+34-26\sqrt{2})∕2=24-13\sqrt{2}$. Cum laturile triunghiului inițial sunt paralele cu laturile noului triunghi și distanța dintre ele este egală cu $1$, centrele celor două cercuri coincid și astfel raza cerută este mai mare cu 1 decât raza aflată, adică $25-13\sqrt{2}$.

Răspuns:

17

Pentru ușurință, vom nota poziția elementelor pornind de la zero. În această situație, prin inducție matematică arătăm că poziția unui număr scris în bază $4$ descrie ce operații (și în ce ordine) au fost aplicate pentru a obține numărul din poziția dată. Spre exemplu, șirul obținut de Marge, după două aplicări a operației de marging, arată astfel:

(Numerele de pe linia inferioară arată poziția rezultatelor în bază $4$.) Cum $2017$ scris în baza $4$ este$133201$, numărul de pe poziția $2017$ este

Răspuns:

25

Privind ecuația dată ca o ecuație de grad doi în necunoscuta $n$, obținem soluția

(cealaltă soluție este negativă deoarece $\sqrt{x^2+y^2}>x$), sau

Fie $d=(x,y)$ și $x=x_{0}d$, $y=y_{0}d$. Prin înlocuire în ecuație, obținem după simplificare

Cum $x_0$ și $y_0$ sunt prime între ele, obținem $y_0^2$ și $x_0^2+y_0^2$ sunt prime între ele, deci $x_0^2+y_0^2\mid n$. În plus, $\sqrt{x_0^2+y_0^2}$ indică faptul că $x_0^2+y_0^2$ trebuie să fie pătrat perfect. Este cunoscut că $5^2=25$ este cel mai mic pătrat perfect care se poate scrie ca sumă de două pătrate perfecte, $3^2+4^2$. Cum $n\ge 25$, prin verificarea în ecuație a valorilor $x=4$, $y=3$, obținem că $n=25$ este valoarea căutată.

Răspuns:

8

Examinând drumurile posibile pe care păianjenul trebuie să le parcurgă, este evident că cel mai scurt este acela în linie dreaptă atunci când camera este desfășurată în plan. Cercul alb reprezintă musca,iar cele negre păianjenul, locația lui în plan depinzând de diferitele moduri în care se poate desfășura încăperea.

Există trei (până la o simetrie) drumuri posibile prin care păianjenul ajunge la muscă, traversând unul, doi sau trei pereți ai camerei; drumurile, în figură, sunt marcate cu $A$, $B$, și $C$. Drumul $A$ este de lungime $8.4m$; folosind teorema lui Pitagora se obține lungimea drumului $B$ egală cu $\sqrt{66.32}m$ și a drumului $C$ egală cu $8m$. Astfel, cel mai scurt drum este $C$, deci răspunsul este $8m.$

Desenul următor arată cel mai scurt drum în trei dimensiuni:

Răspuns:

49

Fie $V(x,y)={(6+2\cos (x)-\cos (y))}^2+{(8+2\sin (x)-\sin (y))}^2$. Să ne reamintim că cercul de centru $[C_1,C_2]$ și rază $R>0$ poate fi parametrizat (adică coordonatele tuturor punctelor de pe cerc pot fi exprimate) prin unghiul $\alpha$ folosind formula $(x_1,x_2)=(C_1+R\cos (\alpha ),C_2+R\sin (\alpha ))$. Să considerăm cercurile $k_1$ și $k_2$ de centre $(0,0)$ și $(6,8)$ și raze $1$ și, respectiv $2$. Atunci, din teorema lui Pitagora, obținem că $V(x,y)=|\mathit{AB}{|}^2$ unde $A\in k_1$ cu unghiul $x$ și $B\in k_2$ cu unghiul $y$. Rezultă că minimul expresiei $V(x,y)$ este pătratul distanței dintre cele mai apropiate puncte de pe cercurile $k_1$ și $k_2$ și poate fi calculată folosind distanța dintre centrele celor două cercuri: $\sqrt{6^2+8^2}-1-2=7$. Astfel minimul expresiei $V(x,y)$ este egal cu $7^2=49$.

Răspuns:

$105263157894736842$

Notăm cu $N$ numărul căutat. Cum $N$ se termină cu $2$, $2N$ se va termina cu $4$, deci cifra zecilor a numărului $N$ este $4$. Fie $d_i$ cifra de pe poziția $i$ din numărul $N$, numărând de la dreapta spre stânga (adică  $d_1$ este cifra unităților). Ținând cont de regulile de modificare a cifrelor unui număr la înmulțirea cu doi, observăm că cifrele numărului $N$ satisfac

pentru toți $i>2$. În acest mod putem să scriem cifrele lui $N$. Ne oprim când obținem cifra $1$ și la pasul următor cifra $2$: numărul care începe cu $1$ este $N$, deoarece prin înmulțirea cu $2$ prima cifră devine $2$, adică ultima cifră din numărul inițial. Numărul căutat este

Răspuns:

$19∕2$

Folosim notațiile din figură.

Din raportul ariilor, $S$ divide $\mathit{QB}$ în raportul $1:2$ și $\mathit{PC}$ în raportul $2:3$. Desenând linia $\mathit{AS}$ și notând aria triunghiului $\mathit{ASQ}$ cu $b$ și aria triunghiului $\mathit{APS}$ cu $a$ obținem următoarea ecuație:

Acestea sunt echivalente cu

de unde se obține soluția $a=5$ și $b=\frac{9}{2}$. Aria porțiunii de pământ $\mathit{APSQ}$ este $\frac{19}{2}$.

Răspuns:

1152

Din moment ce bogăția fiecărui frate este un multiplu al bogăției celor mai săraci, suma lor, $2018$, trebuie să fie divizibilă și prin acest număr. Cu toate acestea, factorizarea inițială $2018=2\cdot 1009$ ne oferă doar trei variante pentru cel mai sărac frate: $1$, $2$, sau $1009$. Evident, $1009$ este imposibil, deoarece acesta ar fi cel mai mare dintre sumele rămase. În plus, dacă este $1$, restul ar rămâne cu $2017$ euro, care este număr prim, deci al doilea frate sărac ar avea tot $1$ euro—contradicție. Din aceste motive, cel mai sărac frate are $2$ euro și ceilalți trei au împreună $2016$.

Fie $a<b<c$ averile celor trei frați; acestea respectă condițiile $a\mid b\mid c$ și $a+b+c=2016$. Divizibilitatea împreună cu stricta inegalitate implică $2a\le b$ și $2b\le c$; dacă am obține egalitate atunci am găsi cea mai mică valoare pentru $c$. Cum, $1+2+4=7$ divide $2016$, putem împărți suma astfel

și răspunsul este $\frac{4}{7}\cdot 2016=1152$.

Răspuns:

1365

Fie $A_n$ secvența de pe tablă ce apare după ce Andrew termină a $n$-a oară procedura (cu $A_0=(♣)$) și $h_n$ numărul de perechi $♡♡$ din $A_n$. Deoarece fiecare pereche $♡♡$ din $A_n$ apare doar din perechea $♡♣$ din $A_{n-1}$, care, pe de altă parte, apare din $♡♡$ sau din $♣$ din $A_{n-2}$, observăm că $h_n=h_{n-2}+2^{n-3}$ pentru $n\ge 3$, deoarece sunt exact $2^{n-3}$ simboluri $♣$ în $A_{n-2}$. Astfel, pentru $n$ impar, avem

deoarece $h_1=0$. Rezultatul cerut este $h_{13}=1365$.

Răspuns:

$10^{\circ }$

Vom arăta că patrulaterul $\mathit{OCNP}$ este inscriptibil; cum $\mathit{\angle ONC}=90^{\circ }$, ar trebui să arătăm că $\mathit{\angle OPC}=90^{\circ }$. Acest lucru rezultă din: punctele $C$ și $M$ se află pe cercul $\varrho$, $\mathit{OC}$ = $\mathit{OM}$. Printr-un calcul simplu, se arată că $\mathit{\angle MOC}=60^{\circ }$, deci $△\mathit{OCM}$ este echilateral. Punctul $P$, fiind mijlocul laturii $\mathit{OM}$, obținem $\mathit{OPC}=90^{\circ }$.

Printr-un calcul simplu se arată că $\mathit{\angle OCN}=70^{\circ }$, de unde $\mathit{\angle OPN}=180^{\circ }-\mathit{\angle OCN}=110^{\circ }$. Folosind triunghiul $\mathit{OQP}$, obținem că

Răspuns:

$(3,2,2013)$

Afirmația Xenei sugerează că $x$ este impar; dacă era par, $y$ și $z$ ar putea fi egale.

Presupunem că $y$ este impar; atunci Yena știa de la început că $x$ și $z$ sunt diferite. Dacă, mai mult, $y\ge 1009$, Yena ar fi știut că $x$ și $z$ sunt diferite de $y$ și nu mai era nevoie de afirmația Xenei. Pe de altă parte, dacă $y\le 1007$, în ciuda afirmației Xenei, Yena nu putea spune dacă numărul ei este diferit de $x$. Deci $y$ este par și $z$ este impar.

Dacă $y$ este multiplu de $4$, atunci $x+z=2018-y\equiv 2(\mathit{mod}4)$, adică ar putea fi dublul unui număr impar; caz în care Yena nu putea deduce că $x$ și $z$ sunt diferite. Mai mult, dacă $y\equiv 2(\mathit{mod}4)$, atunci $x$ și $z$ ar trebui să aibă resturi distincte modulo $4$ și afirmația Yenei este justificată.

În final, să examinăm afirmația Zenei. Mai întâi, $y=2$, pentru că dacă $y$ ar scădea cu $4$ și $x$ ar crește cu $4$ atunci Zena nu ar putea observa diferența. Din motive similare, $x\le 4$, deci $x=1$ sau $x=3$. În primul caz, Zena cunoscând $2018-z=x+y=3$ ar fi putut determina pe $x$ și $y$ fără afirmația Yenei (folosind doar ce Xena a comunicat). Concluzionăm că $x=3$ și $z=2013$.

Răspuns:

$45∕128$

Cantitatea exactă de PL nu este importantă - este suficient să știm că Arithmetix suportă o vrajă și Combinatorica două vrăji. Să presupunem că suntem în stare de duel atunci când ambii vrăjitori îndura doar o vrajă și este rândul lui Arithmetix să arunce o vrajă. Notăm probabilitatea ca Arithmetix să câștige cu $q$. În acest stadiu, Arithmetix poate câștiga fie în cazul în care atacul său reușește, ceea ce se întâmplă cu probabilitatea de $0.9$, sau dacă o ratează și la fel și Combinatorica la rândul său - care se întâmplă cu probabilitatea de $0.1\cdot 0.4$, și ulterior, Arithmetix câștigă din nou cu probabilitate $q$. Prin urmare, obținem ecuația

ce conduce la $q=15∕16$.

Să determinăm acum probabilitatea $p$ ca Arithmetix să câștige duelul. Dacă Arithmetix lovește și Combinatorica ratează (probabilitatea $0.9\cdot 0.4$), duelul ajunge în situația prezentată anterior și Arithmetix câștigă cu probabilitatea $q=15∕16$. Pe de altă parte, dacă Arithmetix ratează și Combinatorica ratează de asemenea (probabilitatea $0.1\cdot 0.4$), atunci Arithmetix poate câștiga cu probabilitatea $p$. Deci putem scrie ecuația

Rezolvând-o, obținem că Arithmetix câștigă duelul cu probabilitatea $p=45∕128$.

Răspuns:

3867

Dacă $a(1)=1$ atunci $a(a(1))=1\ne 3\cdot 1$, ceea ce este imposibil. Deoarece șirul este crescător obținem $1<a(1)<a(a(1))=3$, de unde $a(1)=2$. Din relația dată deducem $a(3n)=a(a(a(n)))=3a(n)$ pentru orice $n$. Se demonstrează ușor prin inducție matematică că pentru orice $m$ avem $a(3^m)=2\cdot 3^m$. Folosind această relație, obținem $a(2\cdot 3^m)=a(a(3^m))=3^{m+1}$. Există $3^n-1$ numere naturale $i$ astfel încât $3^n<i<2\cdot 3^n$ și există $3^n-1$ numere naturale $j$ astfel încât $a(3^n)=2\cdot 3^n<j<3^{n+1}=a(2\cdot 3^n)$. Cum $a(n)$ este crescător, singura opțiune este $a(3^n+b)=2\cdot 3^n+b$ pentru orice $0<b<3^n$. De aceea $a(2\cdot 3^n+b)=a(a(3^n+b))=3^{n+1}+3b$. Cum $2018=2\cdot 3^6+560$ obținem $a(2018)=3^7+3\cdot 560=3867$.

Răspuns:

1346

Fiecărui vârf din rețea i se pot atribui distanțele la cele trei laturi ale triunghiului $T$ (considerând unitatea înălțimea unui triunghi mic); este ușor de observat că pentru fiecare vârf, cele trei numere au suma egală cu $2018$. Pe de altă parte, fiind dat un triplet de numere naturale cu suma $2018$, există un singur vârf din rețea pentru care aceste numere reprezintă distanțele de la el la laturile triunghiului mare, de aceea, putem considera aceste triplete în loc de vârfuri. Vom numi aceste trei numere coordonate.

Condiția de independență a mulțimii este echivalentă cu faptul că oricare două triplete nu sunt egale. Fie

o mulțime independentă. Cum numerele $x_1,\dots ,x_k$ sunt naturale și distincte, suma lor este cel puțin

Analog pentru $y_1+\cdots +y_k$ și $z_1+\cdots +z_k$. Pe de altă parte, avem $x_i+y_i+z_i=2018$ pentru fiecare $i=1,\dots ,k$, și, deci

Obținem că

sau $k\le 1346$.

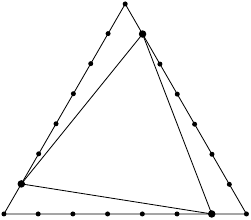
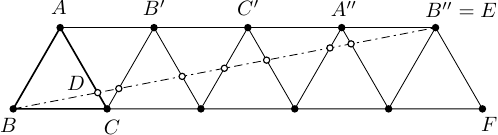
Următoarele două șiruri de puncte formează o mulțime independentă cu $1346$ elemente:

În concluzie, numărul maxim de elemente al unei mulțimi independente este

.

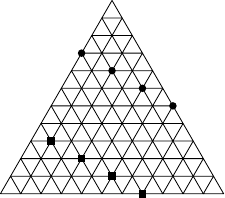
Următorul desen ilustrează construcția unei mulțimi independente a unui triunghi cu latura de lungime $11$:

Răspuns:

$5\sqrt{5∕2}$