Enunțuri probleme

Răspuns:

$6$

Dacă $x$ este vârsta actuală a lui Punto, atunci vârsta actuală a maei sale este $3(x-3)+3$, adică $3x-6$. Vârsta actuală a tatălui lui Punto este $3x$ . Diferența vârstelor părinților este $6$ ani.

Răspuns:

$30$

Toate triunghiurile au vârfurile în cel al figurii. Mai mult, o latură a triunghiurilor este pe una dintre cele două paralele orizontale.Din acest motiv, fiecare triunghi este determinat prin alegerea unui segment de pe cele două paralele determinat de două puncte de pe paralela pe care se află. Cum sunt șase puncte pe fiecare paralelă, numărul triunghiurilor este

Răspuns:

$15$

Cum intr-un triunghi echilateral fiecare unghi are măsura de $60^{\circ }$, obținem că $\mathit{\angle CBE}=90^{\circ }-\mathit{\angle EBA}=30^{\circ }$. Deoarece $\mathit{EB}=\mathit{AB}=\mathit{BC}$, triunghiul $\mathit{BCE}$ este isoscel și astfel

În concluzie $\mathit{\angle DCE}=90^{\circ }-\mathit{\angle ECB}=15^{\circ }$.

Răspuns:

$136$

Pentru siguranță, Sandi ar trebui să scoată toate monedele cu numere mai mici ca 10 și câte nouă monede din fiecare tip inscripționat cu numere de la 10 la 19. În total, $(1+2+\cdots +9)+9\cdot 10=135$.

Când Sandi va scoate și moneda 136, cel puțin $91$ de monede sunt inscripționate cu numere mai mari decât 9. Din principiul cutiei, din unul din cele zece tipuri de monede inscripționate cu numere de la 10 la 19 a cos zece monede.De aceea, numărul minim este $136$.

Răspuns:

$42$

Dacă $n$ este numărul inițial de bomboane, putem scrie distribuția bomboanelor folosind ecuația

Rezolvând-o pentru $n$ obținem $n=42$.

Răspuns:

$24+4\sqrt{6}$

Din teorema lui Pitagora, obținem $\mathit{BD}=\sqrt{6^2+8^2}=10$ și apoi

Aria patrulaterului $\mathit{ABCD}$ este

Răspuns:

$27$

Observăm că Kate vrea să printeze nouă coli. Când printează față-verso, timpul necesar este $9\cdot 9=81$ secunde. Când printează doar față, fiecare coală este prinată de două ori, deci timpul necesar este $2\cdot 3\cdot 9=54$ secunde. În concluzie, timpul necesar reintroducerii foilor în imprimantă este $81-54=27$ secunde.

Răspuns:

$784913526$

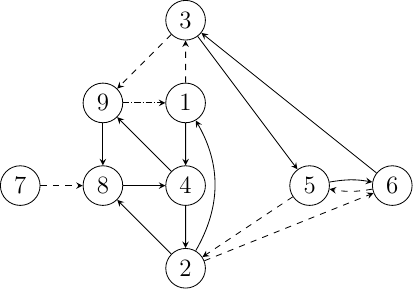
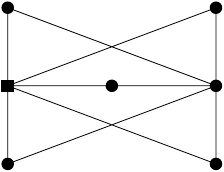
(Săgețile pline definesc divizibilitatea cu $7$, cele cu liniuțe pe cea cu $13$, și cele cu liniuțe și puncte pe cea cu ambele numere.) Din diagramă, este evident că numărul cerut trebuie să înceapă cu $784$. Dacă următoare cifră este $9$, atunci continuăm cu $1$, $3$, și $5$, și ultimele cifre sunt $2$, $6$, în această ordine. Obținem soluția $784913526$.

Dacă, pe de altă parte, începem cu $7842$, rămân de considerat două cazuri. Prima dată, alegând $1$ și, respectiv, $3$, nu se poate ca numărul să conțină cifrele $5$ și $9$. A doua oară, ajungem în aceeași situație dacă alegem $784263$.

Fie $N$ numărul căutat și numim a block numărul de două cifre distincte divizibil cu $7$ sau $13$. Observăm că $78$ este singurul block ce îl conține pe $7$ și $84$ este singurul block ce începe cu $8$, de aceea $N$ trebuie să înceapă cu $784$. Să presupunem că $N$ nu se termină cu $9$; singurele block-uri ce încep cu $9$ sunt $91$ și $98$, și cum poziția lui $8$ în $N$ este deja fixată, $9$ trebuie să fie urmat de $1$. Analog, deoarece $4$ este deja folosit, $1$ trebuie să fie urmat de $3$, $3$ de $5$ etc., formându-se secvența de cifre $913526$, care alăturată lui $784$, oferă răspunsul $N=784913526$.

Dacă cifra unităților lui $N$ este $9$, $N$ trebuie să înceapă cu $7842$ și să se termine cu $39$. $39$ se poate extinde spre stânga folosind $1$ sau $6$, dar, atunci, singurele posibile extensii sunt $2139$, $2639$, și $5639$, primele două conținându-l pe $2$ și ultima nemaiputând fi extinsă spre stânga.

Următoare diagramă arată toate block-urile posibile:

Răspuns:

$54$

Deoarece triunghiurile adiacente pătratului $B$ sunt isoscele, latura lui $B$ de pe diagonală este o treime din diagonală. De aceea, dacă $s$ este lungimea pătratului mare, lungimea laturii lui $B$ este $\frac{1}{3}\cdot \sqrt{2}\cdot s$ și cea a lui $A$ este $\frac{1}{2}\cdot s$. Raportul ariilor pătratelor din interior este

și, astfel, aria pătratului $A$ este $48\cdot \frac{9}{8}=54$.

Răspuns:

$0$

Fiona are $9^3=729$ cuburi albe $10^3=1000$ cuburi negre. Pentru a putea construi un cub cu latura de $12$ are nevoie de $12^3-10^3=1728-1000=728$ cuburi cu latura de 1 cm. În concluzie, poate construi cubul doar cu fețe albe, răspunsul fiind $0$.

Răspuns:

$29$

Pentru a putea determina numărul exact de elevi din clasă, ar trebui să știm și câți elevi au greșit exact două operații pentru fiecare pereche de operații. Observăm că numărul maxim de elevi se obține dacă presupunem că fiecare elev care greșește două operații le greșește pe toate trei. Astfel, numărul total de elevi este

Trebuie să scădem de două ori numărul elevilor care au greșit toate operațiile, deoarece pe aceștia îi numărăm în fiecare dintre cele trei grupe de elevi adunate.

Răspuns:

$44$

Fie $\mathit{ABC}$ triunghiul cu $\mathit{\angle BAC}=90^{\circ }$. Notăm piciorul medianei cu $M$ și cel al înălțimii cu $H$.

Vârfurile triunghiului $\mathit{ABC}$ se găsesc pe un cerc cu centrul în punctul $M$. Deci, fie $\mathit{\angle CBA}=23^{\circ }$. Deoarece triunghiul $\mathit{ABM}$ este isoscel, avem că $\mathit{\angle BAM}=23^{\circ }$. mai mult, triunghiul $\mathit{AHC}$ este asemenea cu triunghiul $\mathit{ABC}$. Astfel $\mathit{\angle HAC}=23^{\circ }$. Obținem $\mathit{\angle MAH}=90^{\circ }-2\cdot 23^{\circ }=44^{\circ }$ ca fiind măsura unghiului căutat.

Răspuns:

$376$

Este evident că $a,b\le 20$. Adunând $b$ în ambii membri ai relației date obținem $20(a+b)=365+b$. Cum membrul stâng se divide cu 20, membrul drept trebuie să fie egal cu 380. Se obține $b=15$, deci $a=4$ și, astfel $20b+19a=380-a=376$.

Răspuns:

$2017$

Prin n puncte necoliniare trei câte trei se pot construi $\frac{n(n-1)}{2}$ drepte. Scăzând numărul de laturi, $n$, obținem numărul de diagonale $\frac{n(n-3)}{2}$. Astfel, $\frac{2019\cdot 2016}{2}-\frac{2018\cdot 2015}{2}=2017$.

Răspuns:

$2$, $5$, $-6$

Cum $x^2-4x+5={(x-2)}^2+1\ge 1$, baza este un număr real pozitiv. Posibilitățile pentru care obținem 1 sunt baza egală cu 1 sau exponentul egal cu 0. În primul caz, $x^2-4x+5=1$ este echivalentă cu ${(x-2)}^2=0$ de unde se obține $x=2$. În a doua situație, din $x^2+x-30=(x-5)(x+6)=0$ obținem soluțiile $x=5$ și $x=-6$.

Răspuns:

$4$

Presupunem că numărul începe cu cifra $1$. Dacă ținem cont de condiția ca cifrele să nu fie în ordine crescătoare, am putea obține $1432$, care după eliminare cifrei $1$ ar avea cifrele în ordine descrescătoare. Ținând cont de simetrie, $1$ nu poate să fie la început sau sfârșit de număr. La fel și pentru $4$. Astfel, cifrele $1$ și $4$ trebuie să fie în mijloc. Avem patru numere care îndeplinesc condițiile cerute:

Răspuns:

$\frac{15}{2}$

Din teorema lui Pitagora, obținem $\mathit{AC}=\sqrt{A{B}^2+B{C}^2}=\sqrt{8^2+6^2}=10$. Fie $S$ mijlocul diagonalei $\mathit{AC}$, deci $\mathit{AS}=5$.

Cum $\mathit{\angle CAB}=\mathit{\angle SAX}$ și $\mathit{\angle XSA}=\mathit{\angle CBA}=90^{\circ }$, triunghiurile $\mathit{ASX}$ și $\mathit{ABC}$ sunt asemenea, obținând $\mathit{SX}:\mathit{AS}=\mathit{BC}:\mathit{AB}$, de unde

Lungimea cerută este $\mathit{XY}=2\cdot \mathit{SX}=\frac{15}{2}$.

Răspuns:

$3435$

Ținând cont de cifra unităților, obținem $R=0$. Cum $\mathit{FIV}E$ se divide cu $5$ și $R=0$, obținem $E=5$. Ținând cont de cifra miilor, obținem $O=9$ și $1$ în minte din adunarea cifrelor zecilor și, iar $1$ din adunarea cifrelor miilor.Deci, $U+V$ trebuie să fie mai mare ca $10$ și $N$ cifră impară. Pe de altă parte, $U+V\le 7+8=15$ deoarece cifra $9$ a fost folosită. Se obține $N=3$. Apoi, $U=6$ (datorită divizibilității cu $4$), $V=7$ și $F=1$.

Cum $\mathit{NINE}$ se divide cu $3$, suma cifrelor $N+I+N+E=3+I+3+5=11+I$ trebuie să se dividă cu $3$. Astfel, $I=4$. De aceea, răspunsul este $\mathit{NINE}=3435$ și relația devine $1960+1475=3435$.

Răspuns:

$3+\sqrt{3}$

Considerăm $G$ intersecție dintre $\mathit{AC}$ și $\mathit{DE}$. Să observăm că cele două triunghiuri dreptunghice $\mathit{BEF}$ și $\mathit{GDC}$ care au unghiurile interioare $30^{\circ }$ și $60^{\circ }$ sunt congruente, deoarece amândouă au o latură egală cu $1$. Acum, un astfel de triunghi este jumătate dintr-un triunghi echilateral ce are lungimea laturii egală cu lungimea ipotenuzei. De aceea, $\mathit{BE}=2\mathit{BF}$ și folosind teorema lui Pitagora $B{E}^2=E{F}^2+B{F}^2$. Ținând cont că $\mathit{EF}=1$, obținem $\mathit{BF}=\sqrt{3}∕3$. De aceea, lungimea laturii triunghiului echilateral $\mathit{ABC}$ este $1+\frac{1}{3}\sqrt{3}$ și perimetrul său este $3+\sqrt{3}$.

Răspuns:

$42$, $-42$

Dacă $r$ este soluție triplă, atunci

de unde $r=\pm 14$. Astfel, avem că $a=\pm 42$.

Răspuns:

$120$

Să observăm că insula pătrată și cea din dreapta din mijloc sunt două insule ’speciale’: Toate podurile încep la una dintre ele, și din orice altă insulă există poduri spre acestea. Deci, întotdeauna vom merge dinspre o insulă specială spre cealaltă traversând o altă insulă. De aceea, tot ce avem de făcut este să ordonăm insulele care nu sunt speciale, lucru ce se poate realiza în $5!=120$ moduri.

Răspuns:

$63$

Distingem două cazuri: Prima dată,să presupunem că niciunul dintre numere nu este egal cu $2000=2^4\cdot 5^3$. Atunci, unul dintre numere este egal cu to $2^4\cdot 5^k$ pentru $k\in \{0,1,2\}$și celălalt este $2^l\cdot 5^3$ pentru $l\in \{0,1,2,3\}$, deci sunt $24$ de perechi (numărând ambele ordonări). A doua oară, dacă unul dintre numere este $2000$, atunci celălalt este un divizor de al lui $2000$ și sunt $(4+1)\cdot (3+1)=20$ de perechi, astfel că, ținând cont de ordine, obținem $2\cdot 20-1=39$perechi; scădem perechea $(2000,2000)$, care este numărată de douaă ori. În total sunt $24+39=63$ perechi.

Răspuns:

$98\sqrt{2}$

Fie $M$ centrul circumscris octogonului. Cum $\mathit{\angle AMC}=\frac{2}{8}\cdot 360^{\circ }=90^{\circ }$, raza cercului este $7$ și diametrul $14$.

Din reanjarea octogonului ca în figură, obținem că aria este egală cu produsul dintre $\mathit{AC}$ și diametru, adică $14\cdot 7\sqrt{2}=98\sqrt{2}$.

Răspuns:

$232$

Să observăm că un triplet de cursuri poate fi urmat de o singură persoană în exact patru moduri. Deci sunt $4^4=256$ moduri ca cei patru să urmeze cursurile nerespectând condiția impusă.

Să numărăm cazurile în care toți cei patru nu au cursuri în comun. Singura posibilitate, pentru fiecare dintre cele patru limbi, este ca unul dintre cei patru să nu aleagă cursul. Deci sunt $4!=24$ alegeri.

Astfel numărul de alegeri ce satisfac condiția dată este $256-24=232$.

Răspuns:

$24,42$

Evident, $n$ are cel puțin două cifre. Dacă $n$ are exact două cifre nenule $a$ și $b$, obținem

sau

Cum membrul drept trebuie să fie pozitiv, obținem $\mathit{ab}<10$. Prin încercări, obținem că $\{a,b\}=\{2,4\}$.

Dacă $n$ are $k\ge 3$ cifre, atunci membrul stâng al egalității este cel puțin ${(10^{k-1})}^2$, în timp ce membrul drept este mai mic decât $1000+10^k$, deci $n$ nu poate avea mai mult de două cifre.

Răspuns:

$110$

Fie $S$ pe $\mathit{BC}$ astfel încât $\mathit{TS}$ este paralel cu $\mathit{AB}$. Atunci $\mathit{\angle ETS}=40^{\circ }$ și

Deoarece $\mathit{CT}$ este bisectoare unghiului $\mathit{\angle DCB}$, triunghiul $\mathit{CTS}$ este isoscel, $\mathit{\angle DCT}=\mathit{\angle TCS}$ și $\mathit{\angle DCB}=2\cdot 35^{\circ }=70^{\circ }$. Atunci $\mathit{\angle CDA}=180^{\circ }-\mathit{\angle DCB}=110^{\circ }$.

Răspuns:

$10$

Fie $m_1$, $m_2$, $w_1$, $w_2$ numărul de bărbați și, respectiv, de femei din casele de nobili. Deoarece $m_1{m}_2=85=5\cdot 17$, observăm că  $m_1=5$ și $m_2=17$ (posibilitatea ca unul dintre numere să fie $1$ se poate exclude imediat). Mai mult, au fost în total $85+162=247$ de plecăciuni, și din

obținem $m_1+w_1=13$, $m_2+w_2=19$ (alte cazuri fiind exceptate ), adică $w_1=8$, $w_2=2$ și răspunsul este $8+2=10$.

Răspuns:

$120∕17$

Din teorema lui Pitagora, obținem că triunghiul este dreptunghic. Segmentul ce unește vârful drept cu centrul cercului împarte triunghiul dreptunghic în două triunghiuri mai mici. Razele duse în punctele de tangență sunt înălțimi în aceste triunghiuri. Fie $r$ raza cercului $c$. Vom calcula aria triunghiului dreptunghic în două moduri, folosind laturile date și triunghiurile mici :

care implică $r=120∕17$.

Răspuns:

$1-\sqrt[19]{0.5}$

Să observăm că Margarita poate pierde de cel mult $19$ ori, deoarece după ce va cheltui ultimul său €$1$ va mai avea doar €$0.5$ , sumă ce este mai mică decât cea pe care aparatul o acceptă. Probabilitatea pentru fiecare pierdere este $1-p$, de aceea probabilitatea ca să nu câștige marele premiu este ${(1-p)}^{19}$. Pentru a vea cel puțin $50\%$ șanse să câștige marele premiu, relația ${(1-p)}^{19}\le 0.5$ trebuie să aibă loc, care este echivalentă cu $p\ge 1-\sqrt[19]{0.5}$ și $1-\sqrt[19]{0.5}$ este cea mai mică valoare posibilă pentru $p$.

Răspuns:

$3435$

Cum $6^6\ge 10000$, cifrele nu pot fi mai mari ca $5$. Dacă toate cifrele ar fi 4, ecuația nu ar avea soluții, și dacă ar fi cel mult trei cifre de $4$, numărul ar fi cel mult $3\cdot 4^4+3^3<1000$. De aceea o cifră trebuie să fie $5$. Deoarece $5^5=3125$, observăm că cifra $5$ trebuie să apară exact o dată, în caz contrar, prima cifră a numărului ar trebui să fie mai mare ca $5$. Cum $3000<5^5<5^5+3\cdot 4^4<4000$, obținem că prima cifră este $3$.

Acum știm că numărul căutat este cel puțin $5^5+3^3+2\cdot 1^1=3154$, care nu verifică ecuația, ca și $3155$. Următorul număr care nu conține cifre mai mari ca $5$ estes $3211>5^5+3\cdot 3^3$, de aceea una dintre cifre trebuie să fie $4$. Nu mai poate fi încă un $4$ deoarece atunci următoarea cifră ar depăși $5$ și rezolvând și următoarele trei cazuri, concluzionăm că numărul căutat este $3435$.

Răspuns:

$16$

Toate cele cinci numere trebuie să aibă ultima cifră pară. Pentru a satisface condiția de non-divizibilitate, numerele ce se termină cu $0$ sau $6$ trebuie să înceapă cu una dintre cifrele $1$, $5$, $7$, cele ce se termină cu $2$ sau $8$ trebuie să înceapă cu una dintre cifrele $3$, $5$, $9$, și cele ce se termină cu $4$ trebuie să înceapă cu una dintre cifrele $1$, $3$, $7$, $9$. Dacă alegem ca numărul care se termină cu $4$ să fie $14$, atunci sunt două alegeri pentru cele ce se termină cu $0$ și $6$ (fie $50$, $76$, fie $56$, $70$), și respectiv, sunt două alegeri pentru cele ce se termină cu $2$ și $8$ (fie $32$, $98$, fie $38$, $92$), deci patru posibilități în total. Un argument similar se aplică pentru orice alegere a numărului ce se termină cu $4$, și cum sunt patru cifre din care putem alege, numărul cvintetelor este $4\cdot 4=16$.

Răspuns:

$5439$

Fie

Evident, $f$ nu este funcție descrescătoare. Mai mult, $f(n)-f(n-1)=1$ dacă $n$ este divizibil cu dintre numerele $5$ sau $7$, și $f(n)-f(n-1)=3$ dacă $n$ este divizibil cu $35$; în orice altă situație $f(n)=f(n-1)$. Cum

obținem

de unde, $n\ge 5436$. $f(5436)=2018$; Cel mai apropiat număr divizibil cu $5$ este $5440$ și cu $7$ este $5439$. $f(5439)=2019$, $f(5440)=2020$, și $5439$ este singura soluție.

Răspuns:

$6$

Cum pentru orice număr natural $a$, $S(a)$ și $a$ au același rest la împărțirea cu $9$, avem că numerele $n$, $x$, $y$, și $x+y$ au același rest la împărțirea cu $9$. Acest lucru implică că $x$ și, respectiv $n$ sunt multipli de $9$. Dacă $n=9m$ cu $m$ număr natural, atunci pentru alegerea $x=y=10^m-1$ obținem egalitatea din enunț. Cea mai mare sumă a cifrelor pentru numere mai mici decât un milion este $54$, de aceea există șase $n$: $9$, $18$, $27$, $36$, $45$, și $54$.

Răspuns:

$\sqrt{5}$

Fie $c$ și $d$ cea mai scurtă și cea mai lungă lungime a proiecțiilor laturilor pătratelor pe laturile dreptunghiului.

Atunci

de unde $c=2$ și $d=1$. Folosind teorema lui Pitagora deducem

Răspuns:

$15∕64$

Putem vedea procesul în felul următor: Paul alege un șir de C și R de lungime totală $(5-1)+(3-1)=6$, și conform lui, el mănâncă coloane sau rânduri din ciocolată. Sunt două posibilități: Ori șirul conține exact doi C (și patru R), caz în care pătratul mai dulce rămâne la final, sau numărul de C și R este cel puțin numărul de coloane și, respectiv, rânduri, care conduce la mâncarea întregii ciocolate. În ultimul caz, ultimul pas nu constă în mâncarea doar a pătratului dulce, nefiind destule coloane sau rânduri mâncate pentru a reduce ultima coloană sau ultimul rând la un singur pătrat.

Sunt $2^6$ șiruri de C și R (de lungime 6) în total, din care $\left(\genfrac{}{}{0.0pt}{}{6}{2}\right)$ conțin exact doi C, deci valoarea probabilității este

Răspuns:

$477$

Nu există numere prime exceptând $2$ și $5$ ce se pot termina cu $5$ sau o cifră pară, de aceea fiecare dintre cifrele

trebuie să fie prima cifră a numerelor scrise. Mai mult, cifrele rămase

trebuie să apară pe poziția unităților. De aceea, suma minimă ce se poate obține este:

Suma este obținută pentru următoarele numere prime:

Răspuns:

1, 5

Descompunând în factori $T(t)-J(j)=0$ obținem $(t+j-3)(t-j+5)=0$ și de aici $\{t,j\}=\{1,2\}$ sau $|t-j|=5$.

Răspuns:

$\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$

Fie $E$ simetricul lui $B$ față de mijlocul $M$ al laturii $\mathit{AC}$ și $F$ piciorul perpendicularei din $E$ pe $\mathit{BC}$. Obținem $\sin (\mathit{\angle EBC})=\frac{\mathit{EF}}{\mathit{BE}}=\frac{1}{2}$ și, deci $\mathit{\angle EBC}=30^{\circ }$ (nu poate fi obtuz datorită celei de a doua condiții). Astfel $\mathit{\angle ABM}=\mathit{\angle ABE}=75^{\circ }-30^{\circ }=45^{\circ }$.

Din teorema sinusurilor aplicată în triunghiurile $\mathit{ABM}$ și $\mathit{CBM}$ obținem

și

Împărțind relațiile ($\mathit{AM}=\mathit{CM}$) și folosind teorema sinusurilor în triunghiul $\mathit{ABC}$ avem

Răspuns:

$32$

Considerăm patru cazuri în funcție de simbolul din mijloc și simbolul care apare de cinci ori în pătrat. Dacă, în mijloc, este un x și sunt cinci de x în pătrat (denumim acest caz “x-x”) trebuie să mai scriem patru de x. Nu putem folosi o întreagă diagonală sau o întreagă “axă”. Avem un model (Figura 1) care nu este simetrică în raport cu o rotație sau axă de simetrie și, de aceea acest caz contribuie cu $8$ modele diferite.

În cazul “x-0” trebuie să desenăm cinci de 0 în pătrat și x în mijloc. Nu putem folosi toate cele patru colțuri deoarece un jucător ar câștiga când am desena al cincilea simbol. Pe de altă parte, trebuie să punem cel puțin un 0 pe ambele diagonale, altfel x câștigă. Astfel, trebuie să desenăm exact trei de 0 sau exact doi de 0 în colțurile pătratului și în ambele cazuri rămâne câte un caz de a umple pătratul. Ambele situații sunt una dintre cele $4$ rotații (ambele au axă de simetrie) ale următoarelor modele (Figura 2 and Figura 3).

Cazurile “0-0” și “0-x” sunt analoage cu cele discutate și astfel, numărul total de umpleri este $2(8+4+4)=32$.

Răspuns:

$32$

Reciproc, obținem

Intervalul dintre $0.72$ și $0.75$ are lungimea $0.03>1∕34$, deci pentru orice $a\ge 34$ avem soluție. Pentru $a=33$ există soluția $b=24$ (obținând $b∕a=0.7272\dots$). Pentru $a=32$ nu există soluție deoarece $24∕32=0.75$ și $1∕32>0.03$.

Răspuns:

$68$, $76$, $91$

Fie $A$, $B$, și $C$ cele trei distanțe măsurate în $\mathrm{km}$. Avem relațiile $2261\mid \mathit{ABC}$ și $2261\mid (110-A)(110-B)(110-C)$. Cum $2261=7\cdot 323=7\cdot 17\cdot 19$ și $7\cdot 17=119>110$ distanțele nu pot fi mai mult decât un factor prim al lui $2261$.

Putem presupune că  $7\mid A$, $17\mid B$, și $19\mid C$. Pentru distanțele $110-A$, $110-B$ and $110-C$, obținem două cazuri $7\mid (110-B)$ și $7\mid (110-C)$ deoarece $7\nmid (110-A)$. În prima situație, $7\mid (110-B)$, obținem $19\mid (110-A)$ și $19\nmid (110-C)$, deci $17\mid (110-C)$. În cazul $7\mid (110-C)$ obținem $17\mid (110-A)$ și $19\mid (110-B)$.

Cum $\mathrm{GCD}(7,19)=1$, singurul mod de descompunere a lui $110$ ca $a\cdot 7+b\cdot 19$ cu $a$, $b$ numere naturale este $110=13\cdot 7+1\cdot 19$ (toate descompunerile sunt de forma $110=(13+19k)\cdot 7+(1-7k)\cdot 19$ pentru $k\in \mathbb{Z}$ și coeficienții sunt naturali doar pentru $k=0$). În mod similar, avem descompunerile $110=4\cdot 17+6\cdot 7$ și $110=4\cdot 19+2\cdot 17$. Acestea conduc la două soluții

și

Remarca lui Heiko din timpul celei de al doilea popas indică faptul că al treilea vârf este la cel puțin $80\mathrm{km}$ depărtare de Passau. În consecinâă, distanțele sunt $68$, $76$ și $91$.

Răspuns:

$3\sqrt{3}∕8$

Observăm că $\mathit{\angle EKA}=90^{\circ }$; iar triunghiurile $\mathit{AEK}$ și $\mathit{ABC}$ sunt congruente, deoarece $\mathit{AK}=\mathit{AC}$, $\mathit{AE}=\mathit{AB}$, și $\mathit{\angle EAK}=\mathit{\angle BAC}$. Centrul $S$ al pătratului $\mathit{ABDE}$ se află pe cercul circumscris triunghiului $\mathit{ABC}$ deoarece $\mathit{ASB}$ și $\mathit{ACB}$ sunt unghiuri drepte. Deoarece $\mathit{AS}=\mathit{BS}$ unghiurile $\mathit{ACS}$ și $\mathit{BCS}$ sunt congruente. De aceea $S$ se află pe bisectoarea $\mathit{CJ}$. Prin relexia triunghiului $\mathit{JKE}$ față de $S$, $E$ ajunge în $B$, $J$ în $H$, care este punctul de intersecție dintre $\mathit{AB}$ și $\mathit{CJ}$, și $K$ ajunge în $I$, care se află pe $\mathit{CJ}$ și satisface $\mathit{\angle IBC}=90^{\circ }$.

Triunghiul $\mathit{IBC}$ este dreptunghic isoscel cu unghiul drept în $B$ și are aria ${(\sqrt{3})}^2∕2=3∕2$. Folosind parateze drepte pentru aria unui triunghi, avem că

Triunghiurile $\mathit{ACH}$ și $\mathit{BIH}$ sunt asemenea, deci

În concluzie,

Răspuns:

$5∕9$

Notăm cu $c$ culoarea extrasă de primul prizonier și cu $o$ cealaltă culoare. Probabilitatea de a extrage din cutia cu $c,c,o$ este $2∕3$ și din cutia cu $c,o,o$ este $1∕3$. Dacă al doilea prizonier alege aceeași cutie ca și primul, acesta va extrage culoarea $c$ cu probabilitatea

și culoarea $o$ cu probabilitatea

Dacă alege cealaltă cutie, extragerea culorii $c$ are probabilitatea

și culoarea $o$

Dacă $c$ este alb, al doilea prizonier va supraviețui dacă extrage $c$. Cume $\frac{4}{9}>\frac{1}{3}$, este indicat să extragă din cealaltă cutie, și va supraviețui cu probabilitatea $\frac{4}{9}$. Dacă $c$ este negru, al doilea prizonier supraviețuiește dacă extrage $o$. Cum $\frac{2}{3}>\frac{5}{9}$, este indicat să aleagă aceeași cutie, și va supraviețui cu probabilitatea $\frac{2}{3}$. Evident $c$ este alb cu probabilitatea $\frac{1}{2}$ și negru cu probabilitatea $\frac{1}{2}$, de aceea al doilea prizonier va supraviețui cu probabilitatea

Răspuns:

$18$

Pentru $n<18$ considerăm primii $n$ termeni ai șirului lui Fibonacci dat prin relația $a_1=a_2=1$, $a_{k+2}=a_{k+1}+a_k$: $1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597$. Evident, cel mai mare număr al oricărui triplet format din aceste numere este mai mare sau egal cu suma celorlalte două și de aceea un astfel de triplet nu poate forma un triunghi nedegenerat. Pentru $n=18$, fie $x_1\le \cdots \le x_{18}$ numerele alese. Dacă oricare trei dintre ele nu formează un triunghi nedegenerat, alegem $x_1,x_2\ge 1$, $x_3\ge x_1+x_2\ge 2,x_4\ge x_3+x_2\ge 2+1=3,\dots$ obținând la fiecare pas un termen din șirul lui Fibonacci terminând cu $x_{18}\ge 987+1597>2019$, ceea ce este imposibil. Numărul cerut este $n=18$.

Răspuns:

$432=2^4\cdot 3^3$

Dacă

este factorizarea lui $n$, atunci

Condiția ca cel mai mare factor să nu putere a lui 2 este echivalentă cu faptul că există un număr impar $q$ care divide $\sigma (n)$ și $\sigma (n^3)$. Cum

acest număr nu se divide cu $3$, și, de aceea cea mai mică valoare pentru $q$ este $5$. Mai mult, $q$ nu poate divide ${\alpha }_i+1$ și $3{\alpha }_i+1$ în același timp, deoarece ar divide

Deci există numerele distincte $i,j\in \{1,\dots ,t\}$ astfel încât $q\mid {\alpha }_i+1$ și $q\mid 3{\alpha }_j+1$. Cum căutăm cel mai mic număr, putem presupune $t=2$, $i=1$, și $j=2$.

Dacă $q=5$, cele mai mici valori pentru ${\alpha }_1$, ${\alpha }_2$ sunt ${\alpha }_1=4$, ${\alpha }_2=3$, și considerând cele mai mici numere prime,  $p_1=2$, $p_2=3$, obținem $n=2^4\cdot 3^3=432$.

Dacă $q\ge 7$, atunci ${\alpha }_1\ge 6$ și ${\alpha }_2\ge 2$, obținându-se

arătând că$432$ este cea mai mică valoare pentru $n$.

Răspuns:

$3\sqrt{5}$

Din teorema catetei obținem

Raza cercului $t$ (care este egală cu $\mathit{DT}$) se poate calcula ca raportul dintre aria triunghiului $\mathit{ACD}$ și semiperimetrul său: Obținem $\mathit{DT}=54∕(36∕2)=3$. Cercul înscris în triunghiul $\mathit{BCD}$, notat cu $\omega$, este tangent laturii $\mathit{CD}$ în $S$. Raza sa este $\mathit{DS}=4$. Omotetia cu centrul în $C$ și raport $\mathit{CT}∕\mathit{CS}=9∕8$ duce cercul $\omega$ în cercul $c$. Astfel, raza cercului $c$ este $4\cdot 9∕8=9∕2$. Fie $M$ mijlocul segmentului $\mathit{XY}$ și $O$ centrul cercului $c$. Știm că $\mathit{XO}=9∕2$ și$\mathit{OM}=\mathit{DT}=3$. Din teorema lui pitagora, obținem că

Răspuns:

$1128$

Din moment ce două pătrățele au colorări diferite, atunci, dacă sunt mai mult de două culori pe o linie există trei pătrățele consecutive colorate prin trei culori diferite. Un astfel de triplet va genera colorarea respectivelor trei coloane. Spre exemplu,  tripletul $1-2-3$ obligă pătrățelele vecine de pe verticală să fie tripletul $3-4-1$ și aceste două triplete trebuie să alterneze până la umplerea coloanelor, conținând doar două culori. Analog pentru coloane în loc de linii. Astfel, nu se pot folosi în același timp mai mult de două culori pe o linie sau două culori pe o coloană.

Presupunem că tabla are $6$ linii și $7$ coloane. Să numărăm colorările folosind doar două culori în fiecare rând: alegem două culori pentru primul rând (atunci cuplul de culori pentru orice alt rând este determinat)și apoi alegem culoarea de început în fiecare din cele $6$ rânduri. Obținem $\left(\genfrac{}{}{0.0pt}{}{4}{2}\right)\cdot 2^6=6\cdot 2^6$ colorări. Analog, numărul colorărilor folosind doar două culori pe fiecare coloană este $6\cdot 2^7$. Trebuie să scădem numărul de colorări cu două culori pe fiecare coloană și pe fiecare linie. Cum o astfel de colorare este determinată de pătratul $2\times 2$ din colțul stâng sus, există $4\cdot 3\cdot 2=24$.

Răspunsul este $6\cdot 2^6+6\cdot 2^7-24=1128$.

Răspuns:

$597+3^{-99}$

După primul pas, al doilea copil are $8+4∕3$. La al doilea pas, al doilea copil oferă o treime din ciocolata sa celui de al treilea, care va avea atunci $12+8∕3+4∕3^2$ grame. După al treilea pas, copilul al patrulea va avea $16+12∕3+8∕3^2+4∕3^3$ grame. Se observă că al $100$-lea copil va avea

Notăm

Atunci avem

Folosind suma numerelor în progresie geometrică,

obținem

În final

Răspuns:

$3,4,5,6,8,14$

Dorim ca $n$ să satisfacă ${(n-2)}^2\mid {(n-1)}^{n-1}-n^2+2019\cdot (n-1)$. Acest lucru nu este influențat de adunarea lui ${(n-2)}^2$ în membrul drept, obținând