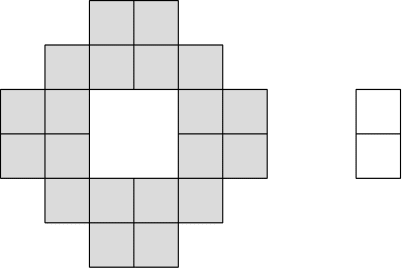
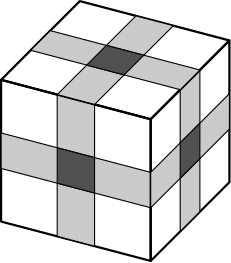
Stavba ima nadstropij. V vsakem nadstropju je hodnik, do katerega se dostopa preko dvojih glavnih vrat in na vsakem hodniku so štiri sobe. Vsaka soba ima svoja vrata, v vsaki sobi pa živi ena oseba. Na vsaka vrata, vključno z vrati hodnika, bo nameščena ena ključavnica, ključi pa bodo razdeljeni tako, da bo veljalo naslednje:
- vsaka oseba lahko dostopa do svoje sobe, vendar ne do sob drugih oseb,
- vsaka oseba lahko dostopa do hodnika v svojem nadstropju,
- dovoljeno je, da ima kdo dostop do hodnikov v drugih nadstropjih.
Vsaka ključavnica je povezana z edinstvenim ključem in se lahko odklene le s tem ključem. Vendar se ista ključavnica lahko po potrebi uporabi na več vratih, izdelati pa je mogoče poljubno število kopij njenega ključa. Posamezniki lahko imajo toliko ključev, kot je potrebno. Podjetje, odgovorno za namestitev, želi minimizirati skupne stroške izdelave ključev. Ustvarjanje novega ključa stane 3, medtem ko izdelava kopije obstoječega ključa stane 2. Kakšen je minimalen skupni strošek vseh ključev ob upoštevanju zgornjih pogojev?Rešitev
Odgovor:
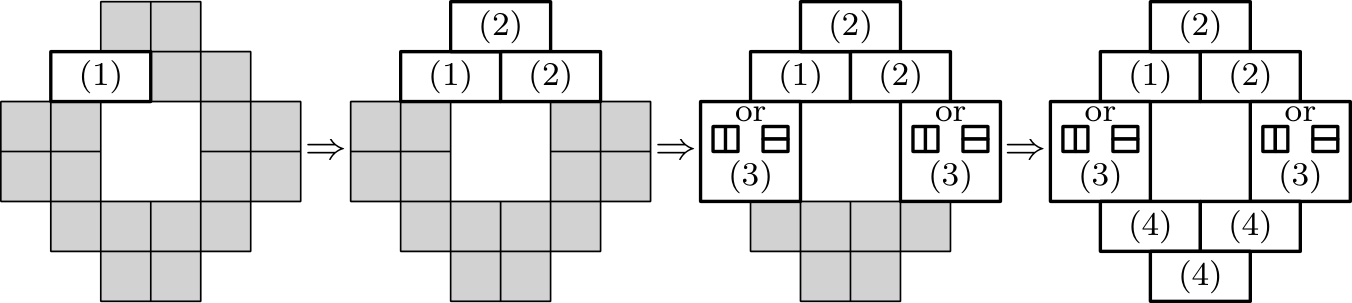
Obravnavajmo čim cenejšo razporeditev ključavnic in ključev; jasno je, da ima v takem primeru vsak stanovalec največ dva ključa. Pokažimo najprej, da lahko predpostavimo, da je v vsakem nadstropju vsaj en stanovalec (oz. natanko en stanovalec, saj več kot en tak ne more obstajati), ki ima natanko en ključ. Ta ključ odklepa tako vrata od njegove sobe kot ena vrata od hodnika, medtem ko ostali stanovalci v tem nadstropju uporabljajo druga vrata, za dostop do hodnika.
Predpostavimo, da v enem nadstropju to ne drži. Potem ena vrata za dostop do hodnika, recimo jim , uporabljata največ dva stanovalca od štirih, ki prebivajo v tem nadstropju - stanovalec in morda stanovalec . Če nihče od štirih stanovalcev nima ključa za vrata , si izberemo poljubnega izmed njih in ga obravnavamo, kot da je stanovalec . Sistem ključev in ključavnic pa spremenimo na sledeč način: Na vratih zamenjamo ključavnico s popolnoma novo ključavnico in enako ključavnico namestimo tudi na vrata sobe stanovalca . Sedaj potrebuje samo en ključ, ki stane , medtem ko je prejšnja konfiguracija z dvema ključema stala vsaj . S tem smo zmanjšali strošek za vsaj .
Če obstaja tudi stanovalec , mu dodelimo ključ za druga vrata od hodnika v tem nadstropju, s čimer nismo povišali stroška. Vendar pa ima sedaj lahko kombinacijo ključev, ki mu omogoča dostop do sobe v kakšnem drugem nadstropju; da bi to popravili, zamenjamo ključavnico na vratih od sobe stanovalca s popolnoma novo ključavnico, s čimer povečamo strošek za največ .
S tem postopkom se skupni strošek za posamezno nadstropje ne poveča, zato lahko zaključimo, da je takšna konfiguracija stroškovno učinkovita, saj zagotovo ne bo dražja od poljubne alternative. V nadaljevanju zato privzamemo, da je v vsakem nadstropju natanko en stanovalec, ki ima samo en ključ.
Problem se torej pretvori na minimizacijo stroškov ključev za 160 nadstropij, kjer ima vsak hodnik le en vhod in tri ločene sobe. Naj bo število različnih tipov ključev, označenih kot . Vsak stanovalec prejme en ključ za svojo sobo in en ključ za hodnik. Ta dva ključa ne moreta biti iste vrste; če bi bil ključ stanovalčeve sobe enak ključu za hodnik, bi ostala dva stanovalca, ki si delita hodniški ključ, bodisi dobila dostop do stanovalčeve sobe bodisi sploh ne bi mogla vstopiti v hodnik. Prav tako nobena dva stanovalca ne smeta imeti istega para ključev, saj bi to pomenilo, da imata dostop do iste sobe. Zato je število veljavnih kombinacij ključev enako .
Ker razdeljujemo skupno parov ključev, določimo spodnjo mejo za iz neenačbe
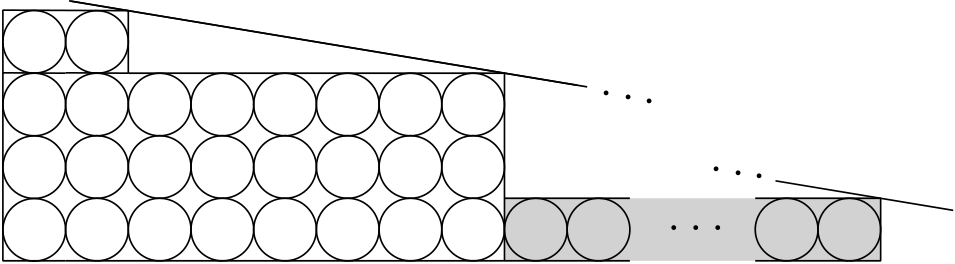
Rešimo za pozitivno celo število in dobimo . Zdaj pokažimo, da je mogoče uporabiti natanko različnih tipov ključev. Da to dosežemo, razdelimo 160 nadstropij v 32 skupin po 5 nadstropij. Razporeditev ključev poteka na naslednji način (prvi ključ v paru je za hodnik, drugi za sobo):
- 15 stanovalcev v prvi skupini prejme pare ključev .
- Druga skupina dobi pare ključev .
- Ta vzorec se nadaljuje, pri čemer 31. skupina prejme pare ključev .
- Na koncu zadnja, 32. skupina, prejme pare ključev .
Zlahka vidimo, da ta razporeditev izpolnjuje dane pogoje. Zato je najmanjše število unikatnih ključev, katerim dodamo še kopij, da pokrijemo vseh ključev. Ob upoštevanju stanovalcev, omenjenih v prvem odstavku, je treba izdelati skupno unikatnih ključev. Tako je končni strošek izračunan kot .