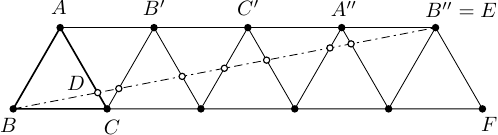
Rovnostranný trojuholník so stranou dĺžky je rozdelený na malých rovnostranných trojuholníkov so stranou dĺžky . Hovoríme, že množina vrcholov týchto rovnostranných trojuholníkov je nezávislá, ak pre ľubovoľné dva rôzne body úsečka nie je rovnobežná so žiadnou stranou . Aký je najväčší možný počet vrcholov v nezávislej množine?Riešenie
Výsledok:
1346
Každému vrcholu v mriežke môžeme priradiť trojicu celých čísel, ktoré sú vzdialenosti tohto vrcholu od troch strán (pričom berieme výšku malého trojuholníka ako jednotku). Je ľahké vidieť, že pre každý vrchol je súčet týchto troch celých čísel . Na druhú stranu, ak si zoberieme trojicu čísel so súčtom , tak je ňou jednoznačne určený vrchol, ktorého vzdialenosti od strán sú tieto čísla. Preto môžeme ekvivalentne uvažovať tieto trojice namiesto vrcholov. Budeme hovoriť o týchto troch číslach ako o súradniciach.
Podmienka nezávislosti sa do reči súradníc preloží tak, že žiadne dve trojice nemajú rovnakú prvú, druhú ani tretiu súradnicu. Nech
|
je nezávislá množina. Keďže čísla sú rôzne nezáporné celé čísla, ich súčet je aspoň
|
To isté platí pre a . Na druhú stranu vieme, že pre všetky , a teda
|
Z toho vyplýva
čiže .
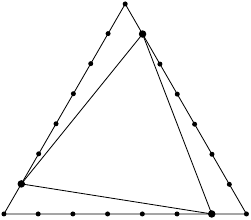
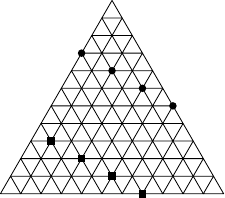
Nasledujúce dve postupnosti spolu tvoria nezávislú množinu veľkosti :
|
Z tohto vyplýva, že maximálny počet vrcholov je
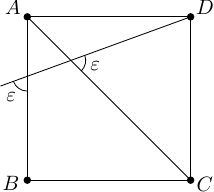
. Na obrázku je znázornená konštrukcia nezávislej množine pre trojuholník so stranou
namiesto
: