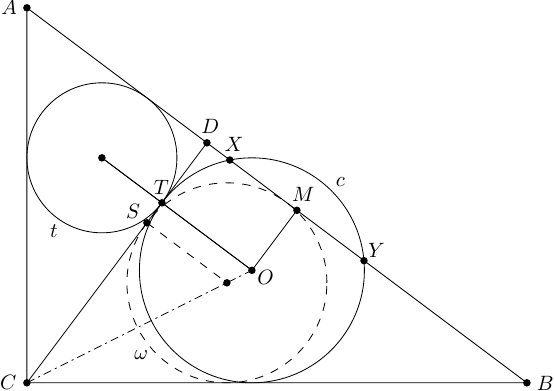
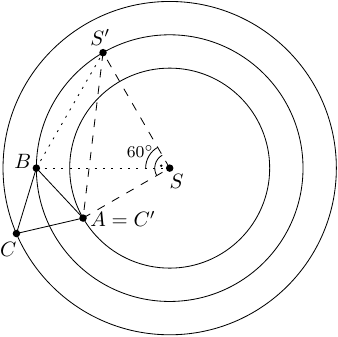
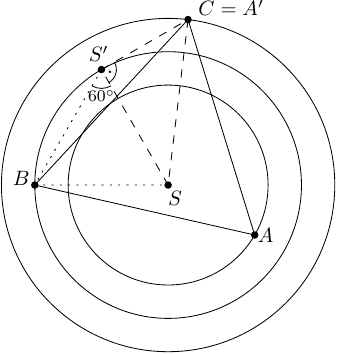
Výsledok:
Vynásobme prvú rovnicu číslom a dosadením z druhej rovnice dostávame: , pričom aj sú prvočísla. Keďže oba výrazy v zátvorkách sú väčšie ako , tak jedna z nich musí byť rovná a druhá musí byť rovná , pričom .
Predpokladajme, že a pre pevné a spĺňajúce . Vyjadríme , a . Môžeme jednoducho overiť, že usporiadaná štvorica
spĺňa druhú rovnicu, teda a je správnym riešením daného systému pre ľubovoľné a . Žiadne dve z týchto riešení nie sú rovnaké. Keby dva páry a dávali to isté vyššie uvedené riešenie, tak z a vyplýva, že a .
Analogicky, pre prípad a získame po dvoch rôznych riešení
pre ľubovoľné a . Žiadne z nájdených riešení v druhom prípade sa nezhoduje a riešením z prvého prípadu, lebo neplatí pre žiadne z možných a . Máme teda spolu štvoríc.