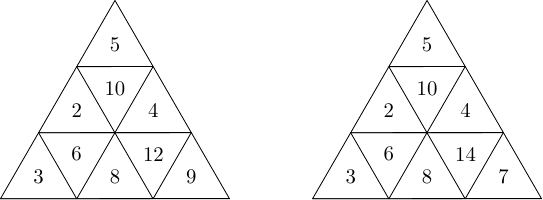
Deliaca postupnosť kladného celého čísla je postupnosť kladných celých čísel takých, že , , splňujú podmienky a . Číslo nazveme vedúcim členom postupnosti. Aký je aritmetický priemer vedúcich členov rôznych postupnosti pre všetky možné deliace postupnosti čísla ?Riešenie
Výsledok:
Máme, že . Keďže pre vedúci člen musia platiť podmienky a , je jasné, že delí . Teraz môžeme hľadať vedúce členy. Ktorékoľvek číslo tvaru , kde je také, že , je vedúcim členom nejakej postupnosti. Existuje osem možných čísel a pre oba a máme dve deliace postupnosti. V prvom prípade je deliacou postupnosťou s a v druhom prípade je to s . Pre ostatné prípady je deliaca postupnosť určená jednoznačne, preto máme možných vodcov. Na nájdenie aritmetického priemeru stačí nájsť .
Všetky postupnosti sú tvaru buď alebo . V prvom prípade máme postupnosti , , , , a v druhom prípade máme postupnosti , , , , .