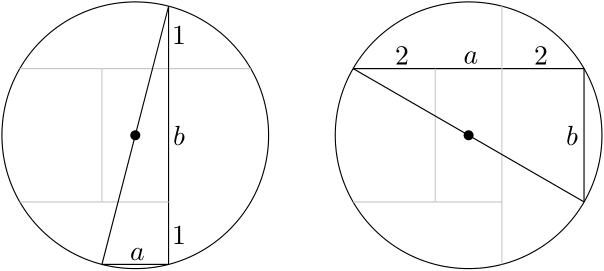
Výsledok:
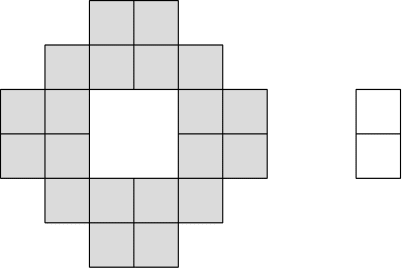
Predpokladajme, že máme nejaký spôsob, ako za najlacnejšiu cenu rozdeliť kľúče. Je zrejmé, že potom žiaden z obyvateľov nemá viac ako dva kľúče. Ďalej ukážeme, že môžeme bez ujmy na všeobecnosti rátať s tým, že na každom poschodí je práve jeden obyvateľ, ktorému stačí prideliť len jeden kľúč. Týmto kľúčom vie odomknúť svoju izbu aj jedny chodbové dvere. Ľahko sa dá premyslieť, že viacerí takí na poschodí byť nemôžu. Ostatní traja následne musia používať druhé chodbové dvere.
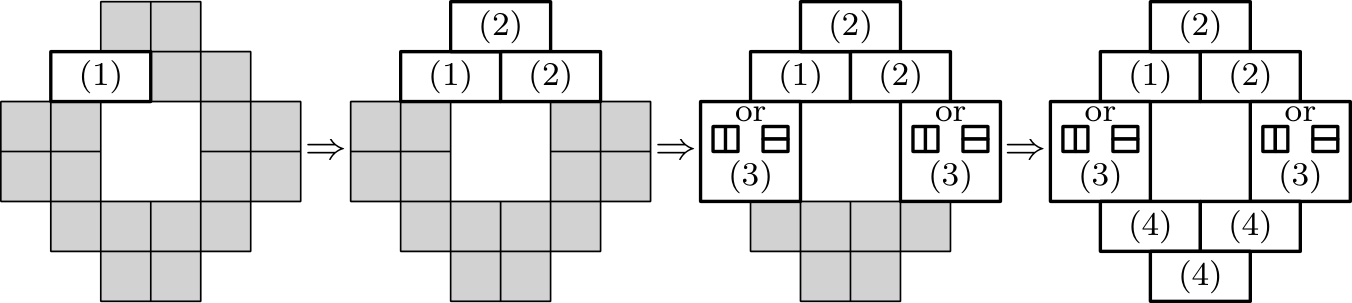
Pre spor predpokladajme, že na nejakom poschodí by to neplatilo. Potom jedny chodbové dvere využívajú najviac dvaja obyvatelia, označme tie dvere a obyvateľov (ak existujú). Ak nevie odomknúť nikto, budeme ďalej ako uvažovať ktoréhokoľvek zo štyroch obyvateľov poschodia. Teraz nahradíme zámok na dverách za úplne nový a rovnaký zámok použijeme aj na dvere izby obyvateľa . Odteraz teda potrebuje iba jeden kľúč v cene , zatiaľ čo jeho predošlé dva kľúče dokopy stáli aspoň . Tým sme znížili celkovú cenu kľúčov o aspoň .
Ak však máme aj obyvateľa , ktorý už teraz nevie odomknúť , nahradíme jeho chodbový kľúč tým od druhých dvier do chodby. Tým cenu nezvýšime, keďže nový chodbový kľúč zrejme môže byť kópiou. Avšak mohlo sa stať, že nadobudol kombináciu kľúčov, ktorá mu umožňuje prístup do cudzej izby. Aby sme tomuto zabránili, nahradíme zámok jeho izbových dvier úplne novým, čo zvýši cenu kľúča najviac o .
Keďže celková cena sa v priebehu procesu nezvyšuje, uvažovaná konfigurácia je aspoň tak lacná ako akákoľvek iná. Preto môžeme predpokladať, že na každom poschodí máme obyvateľa s jediným kľúčom.
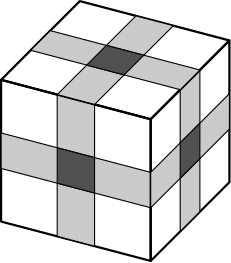
Tým pádom sa nám úloha zjednoduší na hľadanie najmenšej možnej ceny kľúčov v mrakodrape so poschodiami a iba jedným schodiskom, z ktorého na každé poschodie vedú jedny chodbové dvere a na každej chodbe sú iba tri izby.
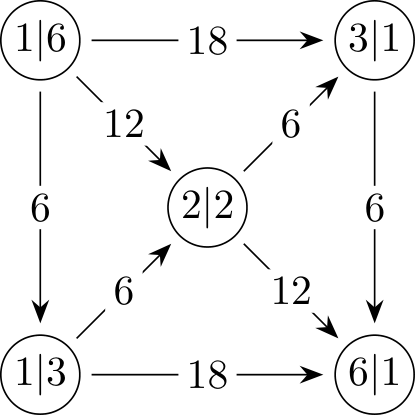
Označme si rozličných typov kľúčov číslami . Každý obyvateľ dostane jeden z kľúčov ku svojej izbe a jeden k chodbe. Tieto kľúče nemôžu byť rovnakého typu, pretože inak by sa mu buď na izbu vedeli dostať aj zvyšní dvaja spolubývajúci z chodby alebo by sa ani nevedeli dostať do svojej chodby. Mimo toho, dvaja ubytovaní nemôžu mať rovnakú dvojicu kľúčov, pretože by tým mali prístup do rovnakej izby. Znamená to teda, že rôznym obyvateľom chceme prideliť rôzne dvojice kľúčov, ktorých počet je .
Keďže potrebujeme vyrobiť dvojice kľúčov pre obyvateľov, dolný odhad na vieme dostať z nerovnice
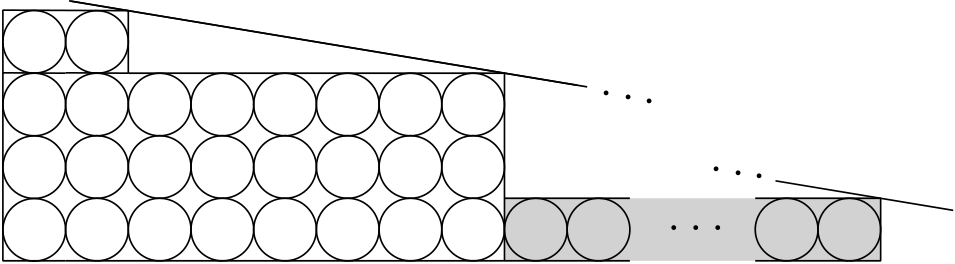
Keď ju vyriešime, prídeme na to, že . Teraz ukážeme, že s rôznymi typmi kľúčov sa nám to už podarí. Na to rozdelíme poschodí do skupín, pričom v každej bude poschodí. Priraďovanie kľúčov (prvý kľúč z páru je chodbový a druhý izbový) prebieha nasledovne:
- 15 obyvateľov v prvej skupine dostane dvojice kľúčov ,
- obyvateľom v druhej skupine dáme dvojice kľúčov ,
- týmto spôsobom pokračujeme až po skupinu, ktorej obyvatelia dostanú , a nakoniec
- poslednej () skupine priradíme dvojice kľúčov .
Nie je náročné vidieť, že takto splníme všetky podmienky uvedené vyššie. Preto je najmenší možný počet jedinečných kľúčov. K nim vytvoríme kópií, čím pokryjeme všetkých kľúčov.
Ešte však potrebujeme započítať obyvateľov s jediným kľúčom z prvého odseku, z čoho dostaneme, že dokopy musí firma vyrobiť jedinečných kľúčov. Preto, výsledná cena je .